第9章 气体动力循环 Gas Power Cycles

热机的分类

应用领域	产生净功率输出	制冷
	发动机	冰箱、空调或热泵
热力学循环	气体循环	蒸汽循环
	工作流体在整个循环中都保持在气态	工作流体在循环的一部分处于蒸汽相，另一部分处于液态
热力学循环	闭式循环	开式循环
	循环结束时，工作流体被返回到初始状态并再循环	每个循环结束时，工作流体都会被更新，而不是被再循环。
热机	内燃机	外燃机

在本章中，我们将在一些简化的假设下分析各种气体动力循环。

理想循环 ideal cycle

理想循环和循环概述

• 当实际循环剥离了所有内部的不可逆性和复杂性后，我们得到的循环很接近实际循环，但完全由内部可逆过程组成。这样的循环被称为理想循环。
• 卡诺循环具有在相同温度水平下运行的所有热引擎的最高热效率。也就是说，没有人能开发出比卡诺循环更有效率的循环。
• 理想循环是内部可逆的，但与卡诺循环不同，它们不一定是外部可逆的。
• 在实践中遇到的大多数循环与卡诺循环有很大的不同，这使得卡诺循环不适合作为一种现实的模型。
• 本章中讨论的每一种理想循环都与特定的工作产生设备有关，并且是实际循环的理想化版本。

理想化假设

1. 循环不涉及任何摩擦。因此，工作流体在管道或如换热器等设备中流动时不会经历任何压力降。
2. 所有的膨胀和压缩过程都以准平衡的方式进行。
3. 连接系统各组件的管道都很好地进行了绝热，通过它们的热传递可以忽略不计。
4. 忽视工作流体的动能和势能的变化。

图表分析

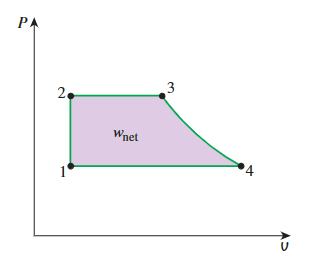
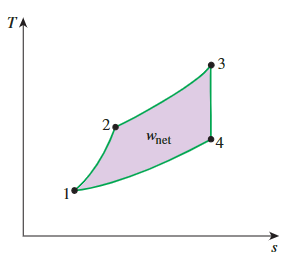
在P-v和T-s图表上，循环过程曲线所**围成的面积代表了循环期间产生的净功，这也相当于该循环的净热传递**。

T-s图表在分析理想动力循环中特别有用。理想动力循环不涉及任何内部不可逆性，所以唯一能改变工作流体在过程中熵的因素是热传递。

在T-s图表上，热添加过程在熵增加的方向进行，热排放过程在熵减少的方向进行。

在T-s图表上，热添加过程下面的面积是在循环期间提供的总热量qin的几何测量，而热排放过程下面的面积是排出的总热量qout的测量。

卡诺循环及其在工程中的价值

THE CARNOT CYCLE AND ITS VALUE

IN ENGINEERING

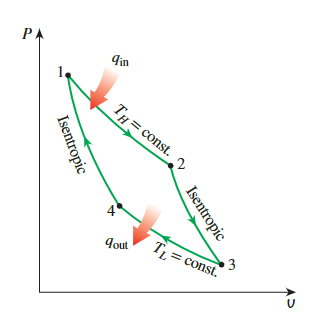
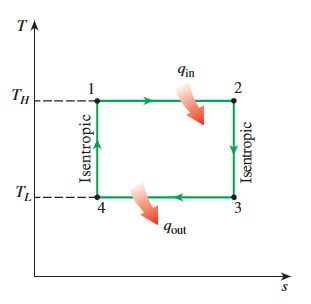
卡诺循环由四个完全可逆过程组成：等温热添加，等熵膨胀，等温热排放，等熵压缩。

其热机效率：

\[ \eta_{\text {th,Carnot }}=1-\frac{T_L}{T_H} \]

在现实中实现可逆等温热传递非常困难

卡诺循环的真正价值在于，它是一个标准，可以与实际或理想循环进行比较。

空气标准假设 **air-standard assumptions**

在气体动力循环中，工作流体在整个循环中始终保持为气态。

实际的气体动力循环相当复杂。为了将分析降到可管理的水平，我们利用了如下的近似，通常被称为空气标准假设：

• 工作流体是**空气**，它在闭环中持续循环，并且始终表现为**理想气体**。
• 构成循环的所有过程都是**内部可逆**的。
• 燃烧过程被替换为**来自外部源的热添加过程**。
• 排气过程被替换为将工作流体恢复到其初始状态的**热排放过程**。

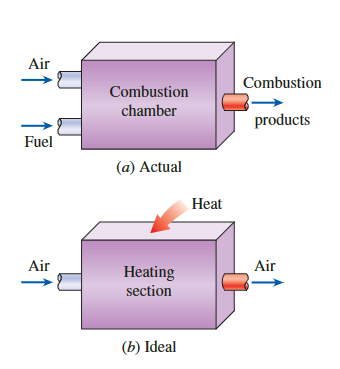
另一个常用的假设是空气的比热容量保持恒定，为其室温（25°C或77°F）下的值。当使用这个假设时，空气标准假设被称为冷空气标准假设**cold-air-standard assumptions**。

往复式发动机概述

RECIPROCATING ENGINES

基本构成

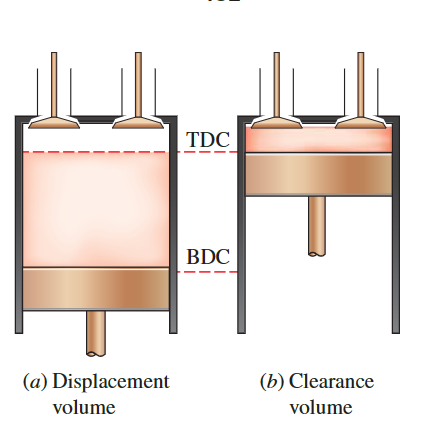
往复式发动机的基本组件如图所示。

• 活塞在气缸中往复运动，运动范围固定在两个位置
  • top dead center顶死点（TDC）-活塞在气缸中形成最小体积的位置
  • bottom dead center底死点（BDC）-活塞在气缸中形成最大体积的位置
• stroke从TDC到BDC的距离是活塞可以在一个方向上行进的最大距离，称为发动机的行程。
• bore活塞的直径称为缸径。
• 空气或空气-燃料混合物通过进气阀intake valve进入气缸
• 燃烧产物通过排气阀exhaust valve从气缸中排出。
• 当活塞在TDC时，气缸中形成的最小体积称为清扫体积clearance volume
• 活塞在从TDC到BDC的移动过程中排出的体积称为排量displacement volume

压缩比

• 气缸中形成的最大体积与最小（清扫）体积的比值称为发动机的压缩比compression ratior：
  • \(r=\frac{V_{\max }}{V_{\text {min }}}=\frac{V_{\mathrm{BDC}}}{V_{\mathrm{TDC}}}\)
  • 注意，压缩比是体积比，不应与压力比混淆。

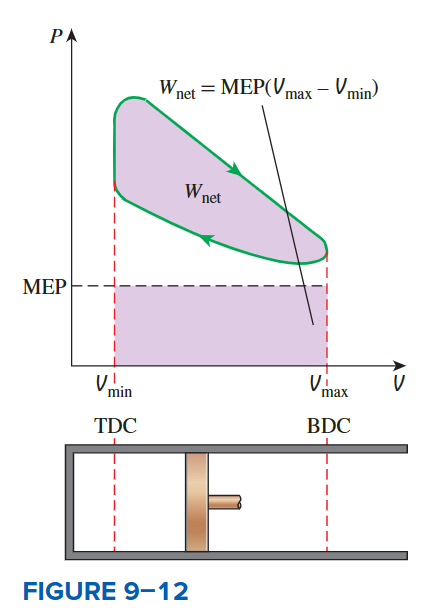
平均有效压力

• 另一个与往复式发动机相关的术语是平均有效压力mean effective pressure（MEP）。MEP是净功和排量之比。

  \[ \mathrm{MEP}=\frac{W_{\text {net }}}{V_{\max }-V_{\text {min }}}=\frac{w_{\text {net }}}{U_{\text {max }}-U_{\text {min }}} \quad(\mathrm{kPa}) \]

  • 平均有效压力可以用作比较同等大小的往复式发动机性能的参数。MEP值较大的发动机每个循环提供的净功更大，因此性能更好。

火花点火和压缩点火

往复式发动机被分类为火花点火（SI）发动机spark-ignition (SI) engines或压缩点火（CI）发动机compression-ignition (CI) engines，这取决于气缸中燃烧过程的启动方式。

奥托循环：火花点火发动机的理想循环

奥托循环是火花点火往复式发动机的理想循环。

发动机结构

四冲程发动机

在大多数火花点火发动机中，活塞在气缸内完成四个完整的冲程（两个机械循环），曲轴完成两个循环的每个热力循环。这些发动机被称为四冲程内燃发动机four-stroke internal combustion engines。

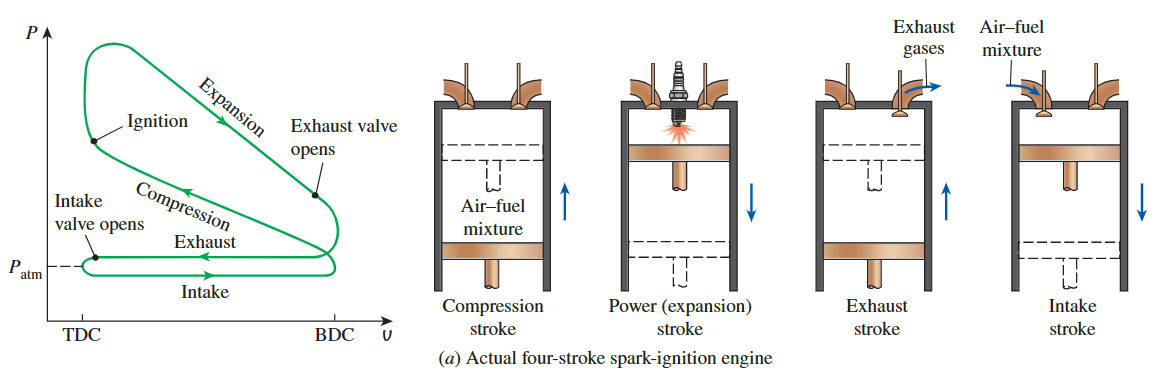
• 请注意，排气冲程期间气缸内的压力略高于大气值，进气冲程期间略低于大气值。

两冲程发动机

在两冲程发动机two-stroke engines中，上述所有四个功能只在两个冲程中执行：动力冲程和压缩冲程。

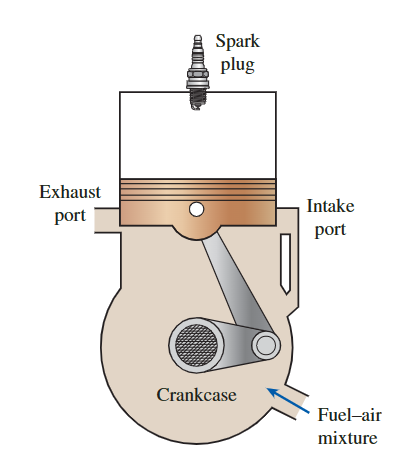
• 在动力冲程的后半部分，活塞首先打开排气口，允许排气气体部分排出，然后打开进气口，允许新鲜的空气-燃料混合物冲入并将气缸中的大部分剩余排气气体驱出。
• 然后在压缩冲程期间压缩这个混合物，活塞向上移动，随后由火花塞点燃。

两冲程发动机通常比它们的四冲程对应型号效率低，这是因为排气气体的不完全排出以及新鲜空气-燃料混合物与排气气体的部分排出。

然而，它们相对简单且成本低廉，且具有高的功率-重量和功率-体积比，这使它们适用于需要小尺寸和重量的应用，如摩托车、链锯和割草机。

发动机原理分析

利用空气-标准假设，分析可以被显著地简化。由此产生的循环是理想的奥托循环。它由四个内部可逆过程组成：

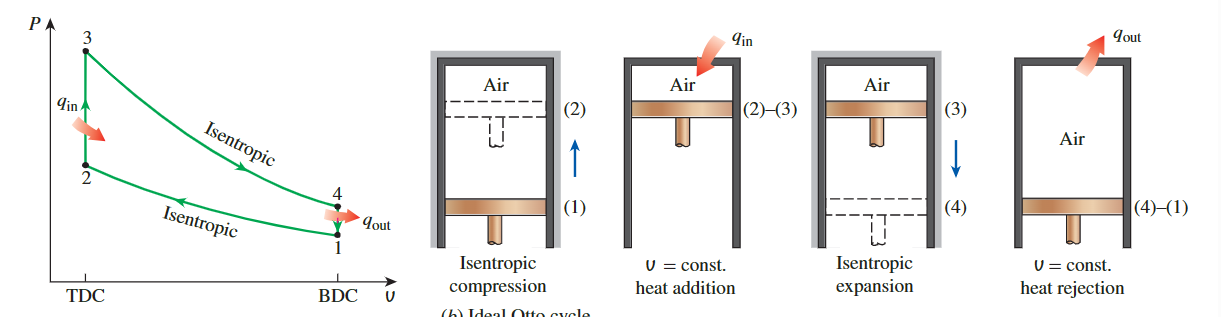
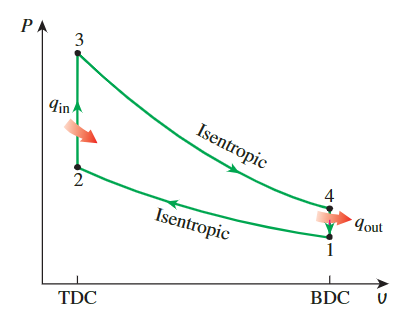
• 1-2 等熵压缩Isentropic compression
• 2-3 等体积热添加Constant-volume heat addition
• 3-4 等熵膨胀Isentropic expansion
• 4-1 等体积热排放Constant-volume heat rejection

奥托循环在活塞-气缸装置中的执行以及P-v图如图9-13b所示。奥托循环的T-s图是

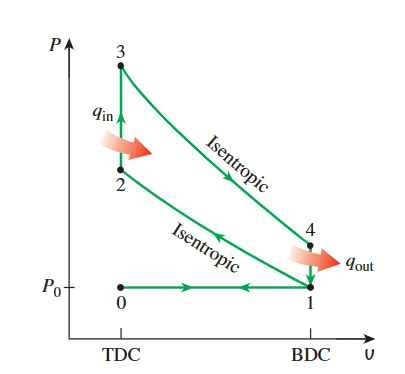
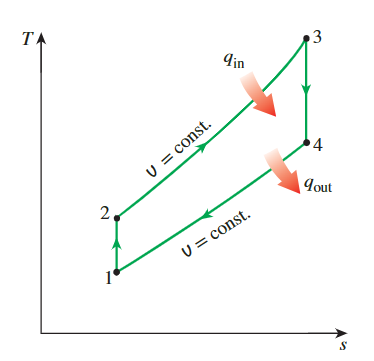
• 0-1空气-燃料混合物（由于空气标准假设，近似为空气）通过开放的进气阀在大气压力 P0 下进入气缸，活塞从TDC移动到BDC。
• 1-2在状态1，关闭进气阀，空气等熵压缩到状态2。
• 2-3热量在恒定体积下传递
• 3-4等熵膨胀到状态4
• 4-1并且热量在恒定体积下排出。
• 1-0排出气体（再次近似为空气）通过开放的排气阀排出（过程1-0），压力保持在 P0 常数。

进气和排气

\[ \begin{aligned}& w_{\text {out }, 0-1}=P_0\left(U_1-U_0\right) \\& w_{\text {in }, 1-0}=P_0\left(U_1-U_0\right)\end{aligned} \]

这两个过程相互抵消，进气期间的功率输出等于排气期间的功率输入。因此，进气和排气过程对循环的净功率输出没有影响。在计算时忽略这一部分是可能的。

奥托循环

忽略动能和势能的变化

\[ \left(q_{\text {in }}-q_{\text {out }}\right)+\left(w_{\text {in }}-w_{\text {out }}\right)=\Delta u \quad(\mathrm{~kJ} / \mathrm{kg}) \]

• 两个热传递过程中不做功，因为两者都在恒定体积下进行。

  \[ \begin{aligned}q_{\text {in }}=u_3-u_2=c_v\left(T_3-T_2\right)\\q_{\mathrm{out}}=u_4-u_1=c_{\mathrm{v}}\left(T_4-T_1\right)\end{aligned} \]

• 然后，在冷空气标准假设cold air standard assumptions下，理想奥托循环的热效率变为

\[ \eta_{\mathrm{th}, \mathrm{Otto}}=\frac{w_{\text {net }}}{q_{\mathrm{in}}}=1-\frac{q_{\mathrm{out}}}{q_{\mathrm{in}}}=1-\frac{T_4-T_1}{T_3-T_2}=1-\frac{T_1\left(T_4 / T_1-1\right)}{T_2\left(T_3 / T_2-1\right)} \]

• 过程1-2和3-4是等熵的，v2 = v3 和 v4 = v1。因此

\[ \frac{T_1}{T_2}=\left(\frac{U_2}{U_1}\right)^{k-1}=\left(\frac{U_3}{U_4}\right)^{k-1}=\frac{T_4}{T_3} \]

• 得到：

  \[ \eta_{\text {th,Otto }}=1-\frac{1}{r^{k-1}},\quad r=\frac{V_{\max }}{V_{\min }}=\frac{V_1}{V_2}=\frac{U_1}{U_2} \]

  • k 是比热比 \(c_p/c_v\)

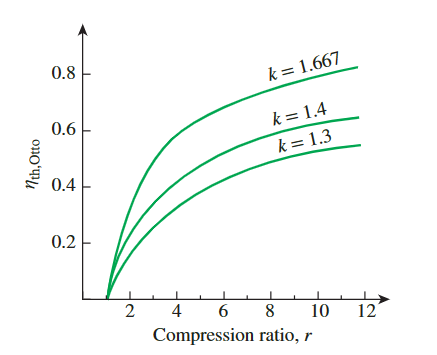
• 方程表明，在冷空气标准假设下，理想奥托循环的热效率取决于引擎的压缩比和工作流体的比热比。理想奥托循环的热效率随压缩比和比热比的增加而增加。

示例：The Ideal Otto Cycle

一个理想的奥托循环的压缩比为8。在压缩过程开始时，空气的压力为100 kPa，温度为17°C，在恒定体积加热过程中，向空气传递了800 kJ/kg的热量。

假设该循环在一个有四个气缸、总排量为1.6 L的发动机上运行。

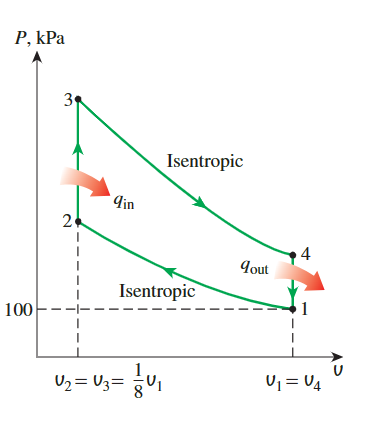
根据空气比热随温度变化的情况，确定

• 1. 循环过程中出现的最高温度和压力
• 2. 净功率输出
• 3. 热效率
• 4. 循环的平均有效压力。
• 5. 在发动机转速为4000 rpm（rev/min）时，循环的功率输出，以kW为单位。

**解答**：考虑一个理想的奥托循环。需要确定的是最高温度和压力，净功率输出，热效率，平均有效压力，以及给定发动机转速的功率输出。

An ideal Otto cycle is considered. The maximum temperature and pressure, the net work output, the thermal efficiency, the mean effective pressure, and the power output for a given engine speed are to be determined.

**假设**：

• 应用空气-标准假设。
• 动能和势能的变化可以忽略。
• 要考虑比热随温度变化的情况。

The air-standard assumptions are applicable.

Kinetic and potential energy changes are negligible.

The variation of specific heats with temperature is to be accounted for.

**分析**：如图9所示的理想奥托循环的P-v图。气缸中的空气形成了一个封闭系统。

**(a)** 奥托循环中的最高温度和压力出现在恒定体积加热过程的结束时（状态3）。但首先，我们需要确定在等熵压缩过程结束时（状态2）空气的温度和压力，使用表A-17的数据：

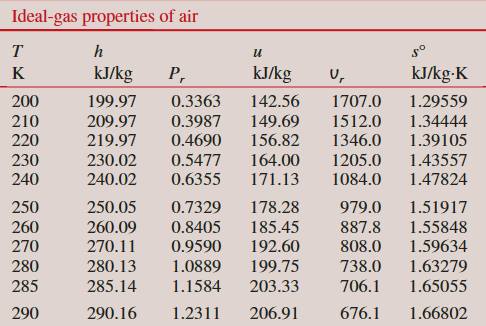
\[ \begin{aligned}T_1=290 \mathrm{~K} \rightarrow u_1 & =206.91 \mathrm{~kJ} / \mathrm{kg} \\U_{r 1} & =676.1\end{aligned} \]

过程1-2（理想气体的等熵压缩）：

\[ \begin{aligned}& \frac{U_{r 2}}{U_{r 1}}=\frac{U_2}{U_1}=\frac{1}{r} \rightarrow U_{r 2}=\frac{U_{r 1}}{r}=\frac{676.1}{8}=84.51 \rightarrow T_2=652.4 \mathrm{~K} \\& u_2=475.11 \mathrm{~kJ} / \mathrm{kg} \\& \frac{P_2 U_2}{T_2}=\frac{P_1 U_1}{T_1} \rightarrow P_2=P_1\left(\frac{T_2}{T_1}\right)\left(\frac{U_1}{U_2}\right) \\& =(100 \mathrm{kPa})\left(\frac{652.4 \mathrm{~K}}{290 \mathrm{~K}}\right)(8)=1799.7 \mathrm{kPa} \\&\end{aligned} \]

过程2-3（恒定体积加热）：

\[ \begin{aligned}q_{\text {in }} & =u_3-u_2 \\800 \mathrm{~kJ} / \mathrm{kg} & =u_3-475.11 \mathrm{~kJ} / \mathrm{kg} \\u_3 & =1275.11 \mathrm{~kJ} / \mathrm{kg} \rightarrow T_3=\mathbf{1 5 7 5 . 1} \mathbf{~ K} \\& U_{r 3}=6.108\end{aligned} \]

\[ \begin{aligned} \frac{P_2 U_2}{T_2}=\frac{P_1 U_1}{T_1} \rightarrow P_2 & =P_1\left(\frac{T_2}{T_1}\right)\left(\frac{U_1}{U_2}\right) \\ & =(100 \mathrm{kPa})\left(\frac{652.4 \mathrm{~K}}{290 \mathrm{~K}}\right)(8)=1799.7 \mathrm{kPa} \end{aligned} \]

**(b)** 循环的净功率输出可以通过求解每个过程的边界（P dV）功并将它们加起来，或找出等效于循**环过程中净热量传递**。 过程3-4（理想气体的等熵膨胀）：

\[ \begin{aligned}\frac{U_{r 4}}{U_{r 3}}=\frac{U_4}{U_3}=r \rightarrow U_{r 4}=r U_{r 3}=(8)(6.108)=48.864 \rightarrow T_4 & =795.6 \mathrm{~K} \\u_4 & =588.74 \mathrm{~kJ} / \mathrm{kg}\end{aligned} \]

过程4-1（恒定体积排热）：

\[ \begin{gathered}-q_{\text {out }}=u_1-u_4 \rightarrow q_{\text {out }}=u_4-u_1 \\q_{\text {out }}=588.74-206.91=381.83 \mathrm{~kJ} / \mathrm{kg} \\w_{\text {net }}=q_{\text {net }}=q_{\text {in }}-q_{\text {out }}=800-381.83=418.17 \mathrm{~kJ} / \mathrm{kg}\end{gathered} \]

**(c)** 循环的热效率可以从其定义中得到：

\[ \eta_{\mathrm{th}}=\frac{w_{\text {net }}}{q_{\text {in }}}=\frac{418.17 \mathrm{~kJ} / \mathrm{kg}}{800 \mathrm{~kJ} / \mathrm{kg}}=0.523 \text { or } 52.3 \% \]

根据冷空气-标准假设（室温下的恒定比热值）the cold-air-standard assumption，热效率将是

\[ \eta_{\mathrm{th}, \mathrm{Otto}}=1-\frac{1}{r^{k-1}}=1-r^{1-k}=1-(8)^{1-1.4}=0.565 \text { or } 56.5 \% \]

这与上面获得的值相差很大。因此，在使用冷空气-标准假设时应小心。

**(d)** 平均有效压力是根据其定义来确定的：

\[ \mathrm{MEP}=\frac{w_{\text {net }}}{v_1-v_2}=\frac{w_{\text {net }}}{v_1-v_1 / r}=\frac{w_{\text {net }}}{v_1(1-1 / r)} \]

其中

\[ U_1=\frac{R T_1}{P_1}=\frac{\left(0.287 \mathrm{kPa} \cdot \mathrm{m}^3 / \mathrm{kg} \cdot \mathrm{K}\right)(290 \mathrm{~K})}{100 \mathrm{kPa}}=0.8323 \mathrm{~m}^3 / \mathrm{kg} \]

因此

\[ \mathrm{MEP}=\frac{418.17 \mathrm{~kJ} / \mathrm{kg}}{\left(0.8323 \mathrm{~m}^3 / \mathrm{kg}\right)\left(1-\frac{1}{8}\right)}\left(\frac{1 \mathrm{kPa} \cdot \mathrm{m}^3}{1 \mathrm{~kJ}}\right)=574 \mathrm{kPa} \]

5. 所有四个气缸在充电时接收的总空气质量为

\[ m=\frac{V_d}{U_1}=\frac{0.0016 \mathrm{~m}^3}{0.8323 \mathrm{~m}^3 / \mathrm{kg}}=0.001922 \mathrm{~kg} \]

循环产生的净功为

\[ W_{\text {net }}=m w_{\text {net }}=(0.001922 \mathrm{~kg})(418.17 \mathrm{~kJ} / \mathrm{kg})=0.8037 \mathrm{~kJ} \]

即，每个热力循环产生的净功为0.8037千焦耳/循环。注意在四冲程发动机中，每个热力循环有两个转动（\(n_{rev} = 2 rev/cycle\)），发动机产生的功率是

\[ \dot{W}_{\text {net }}=\frac{W_{\text {net }} \dot{n}}{n_{\text {rev }}}=\frac{(0.8037 \mathrm{~kJ} / \text { cycle })(4000 \mathrm{rev} / \mathrm{min})}{2 \mathrm{rev} / \text { cycle }}\left(\frac{1 \mathrm{~min}}{60 \mathrm{~s}}\right)=26.8 \mathrm{~kW} \]

柴油循环：压燃发动机的理想循环

发动机结构

压燃式点火方式

柴油循环是往复式压燃发动机的理想循环。在压燃发动机（也称为柴油发动机）中，空气被压缩到高于燃料自燃温度的温度，当燃料喷入这个热空气中时，燃烧开始。因此，柴油发动机中的火花塞被燃油喷射器取代。

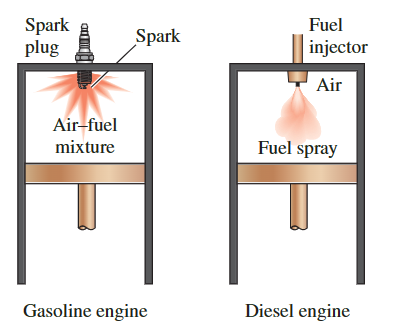
柴有发动机不需要考虑其自燃，使得柴油发动机可以设计为以更高的压缩比运行。此外，许多对汽油提出的严格要求现在可以取消，柴油发动机可以使用较少提炼（因此较便宜）的燃料。

热力学循环

柴油发动机中的燃油喷射过程在活塞接近顶死点时开始，并在功率行程的第一部分继续。这些发动机中的燃烧过程在更长的时间内进行。因此，**理想柴油循环中的燃烧过程被近似为恒压加热过程**。 实际上，这是奥托循环和柴油循环的唯一区别。

• 1-2是等熵压缩
• 2-3是恒压加热
• 3-4是等熵膨胀
• 4-1是恒容排热。

从柴油循环的P-v和T-s图中也可以看出两个循环的相似性

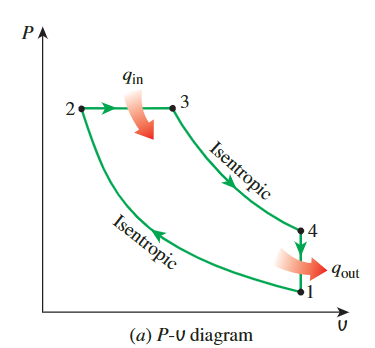
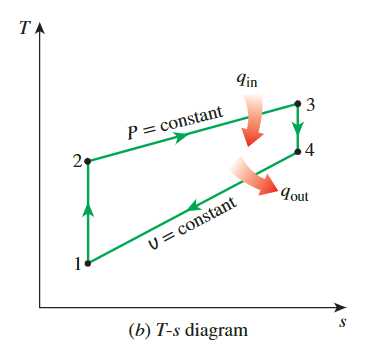
热力学原理

热力学效率

注意到柴油循环是在活塞-缸装置中执行的，该装置形成了一个封闭系统，可以表示为在恒压下向工作流体传递的热量和在恒容下从其排出的热量

\[ \begin{aligned}q_{\text {in }}-w_{b, \text { out }}=u_3-u_2 \rightarrow q_{\text {in }} & =P_2\left(\cup_3-v_2\right)+\left(u_3-u_2\right) \\& =h_3-h_2=c_p\left(T_3-T_2\right)\end{aligned} \]

和

\[ -q_{\mathrm{out}}=u_1-u_4 \rightarrow q_{\mathrm{out}}=u_4-u_1=c_{\mathrm{v}}\left(T_4-T_1\right) \]

然后，在冷空气标准假设下，理想柴油循环的热效率变为

\[ \eta_{\text {th,Diesel }}=\frac{w_{\text {net }}}{q_{\text {in }}}=1-\frac{q_{\text {out }}}{q_{\text {in }}}=1-\frac{T_4-T_1}{k\left(T_3-T_2\right)}=1-\frac{T_1\left(T_4 / T_1-1\right)}{k T_2\left(T_3 / T_2-1\right)} \]

截至比率 **cutoff ratio r**

\[ r_c=\frac{V_3}{V_2}=\frac{U_3}{U_2} \]

由此定义热机效率：

\[ \eta_{\text {th,Diesel }}=1-\frac{1}{r^{k-1}}\left[\frac{r_c^k-1}{k\left(r_c-1\right)}\right]，r_c=\frac{V_3}{V_2}=\frac{U_3}{U_2} \]

实例

教材《Thermodynamics, an engineering approach 9ed》的\(P_{491}\)有理想柴油机的实例，在此不再赘述。

斯特林和埃里克森循环

理想奥托和柴油循环完并不完全可逆，因为它们在非等温的加热和排热过程中通过有限的温差进行热量传递，这是不可逆的。因此，奥托或柴油发动机的热效率将低于在同样的温度限制下运行的卡诺发动机的热效率。

有两种循环涉及到在\(T_H\)处进行等温加热过程和在\(T_L\)处进行等温排热过程：斯特林循环和埃里克森循环。

它们与卡诺循环的不同之处在于，斯特林循环中的两个等熵过程被两个恒容再生过程取代，而在埃里克森循环中，这两个等熵过程被两个恒压再生过程取代。

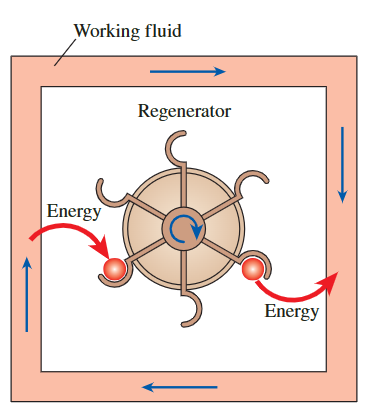
这两种循环都利用了再生regeneration，即在循环的一部分过程中，热量被转移到热能存储设备（称为再生器），在循环的另一部分过程中，热量被转回到工作流体。

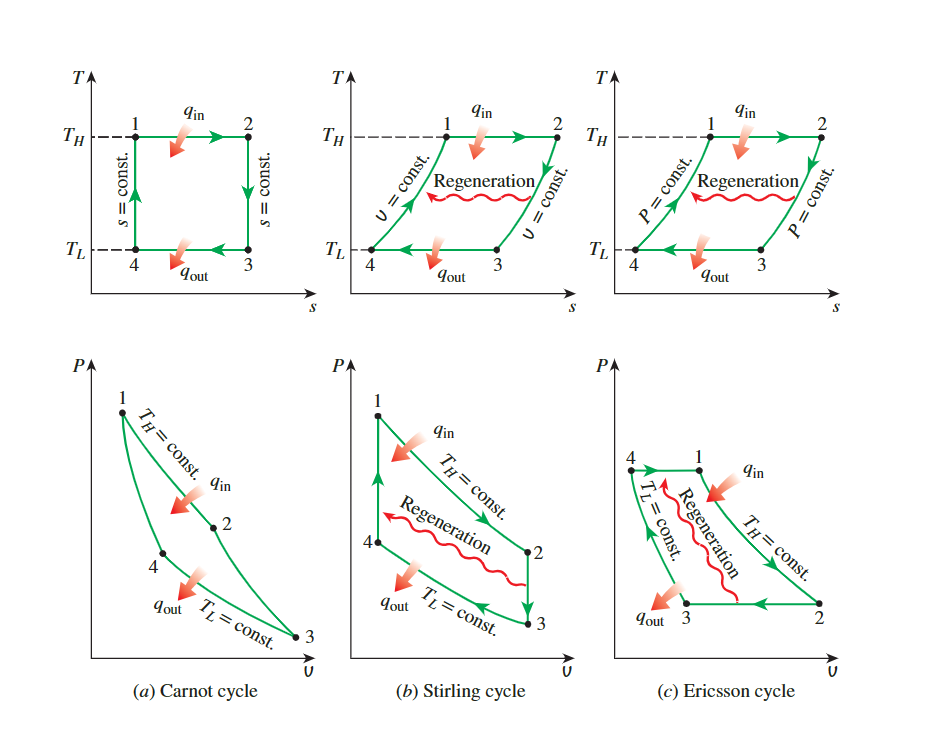
斯特林循环 **Stirling cycle**

循环过程

上图显示了斯特林循环的T-s和P-v图，由四个完全可逆的过程组成：

1-2 \(T = constant\) **扩展**（从外部源加热） 2-3 \(v = constant\) **再生**（内部热量从工作流体转移到再生器） 3-4 \(T = constant\) **压缩**（向外部汇排热） 4-1 \(v = constant\) **再生**（内部热量从再生器回到工作流体）

循环系统

斯特林循环的执行需要相当创新的硬件。我们将借助图中显示的假想引擎来解释在封闭系统中执行斯特林循环。

该系统由一个气缸组成，气缸的两侧各有一个活塞，中间有一个再生器。再生器可以是线材或陶瓷网状物或具有高热质量（质量乘以比热）的任何类型的多孔塞。它用于临时存储热能。

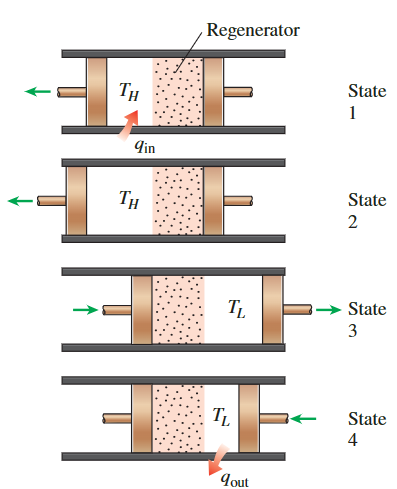
• 最初，左侧腔室容纳了所有的工作流体（气体），该气体处于高温和高压。
• 在过程1-2中，热量从温度为T_H的源头转移到气体。由于气体在等温下膨胀，左活塞向外移动，做功，并且气体压力下降。
• 在过程2-3中，两个活塞以相同的速率向右移动（保持体积不变），直到整个气体被强制进入右腔。随着气体通过再生器，热量转移到再生器并且气体温度从T_H下降到T_L。
• 在过程3-4中，右活塞向内移动，压缩气体。热量从气体传递到温度为T_L的汇，使得在压力上升时气体温度保持在T_L。
• 最后，在过程4-1中，两个活塞以相同的速度向左移动（保持体积不变），将整个气体强制进入左腔。随着气体通过再生器并吸收在过程2-3中存储在那里的热能，气体温度从T_L升高到T_H。这完成了循环。

注意，第二个恒容过程发生在体积比第一个小的地方，而再生器在一个周期中的净热量传递为零。也就是说，过程2-3中存储在再生器中的能量量等于过程4-1中气体吸收的量。

埃里克森循环 **Ericsson cycle**

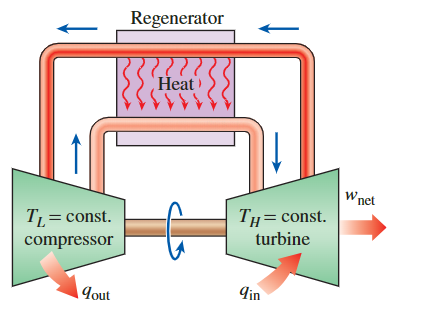
Ericsson 循环的 T-s 和 P-v 图如上图c 所示。 Ericsson 循环非常类似于 Stirling 循环，只是将两个恒定体积过程替换为两个恒定压力过程。 一个执行 Ericsson 循环的稳流系统如下图所示。

效率

Stirling 循环和 Ericsson 循环都是完全可逆的，Carnot 循环也是如此，因此根据 Carnot 原理，当在相同的温度限制下运行时，所有三个循环必须具有相同的热效率：

\[ \eta_{\text {th,Stirling }}=\eta_{\text {th,Ericsson }}=\eta_{\text {th,Carnot }}=1-\frac{T_L}{T_H} \]

证明

使用理想气体作为工作流体，表明在相同的温度极限之间运行的Erics-son循环的热效率与Carnot循环的效率相同

• 对于两个绝热过程，熵变：

\[ \Delta s=c_p \ln \frac{T_e^0}{T_i}-R \ln \frac{P_e}{P_i}=-R \ln \frac{P_e}{P_i} \]

• 由此，其热输入和热输出：

\[ \begin{gathered}q_{\text {in }}=T_H\left(s_2-s_1\right)=T_H\left(-R \ln \frac{P_2}{P_1}\right)=R T_H \ln \frac{P_1}{P_2} \\q_{\text {out }}=T_L\left(s_4-s_3\right)=-T_L\left(-R \ln \frac{P_4}{P_3}\right)=R T_L \ln \frac{P_4}{P_3}\end{gathered} \]

• 其热效率

\[ \eta_{\text {th,Ericsson }}=1-\frac{q_{\text {out }}}{q_{\text {in }}}=1-\frac{R T_L \ln \left(P_4 / P_3\right)}{R T_H \ln \left(P_1 / P_2\right)}=1-\frac{T_L}{T_H} \]

• 对于斯特林循环，只需要利用理想气体把压力比转换为体积比

布雷顿循环：燃气轮机发动机的理想循环

一般的布雷顿循环

基本构成

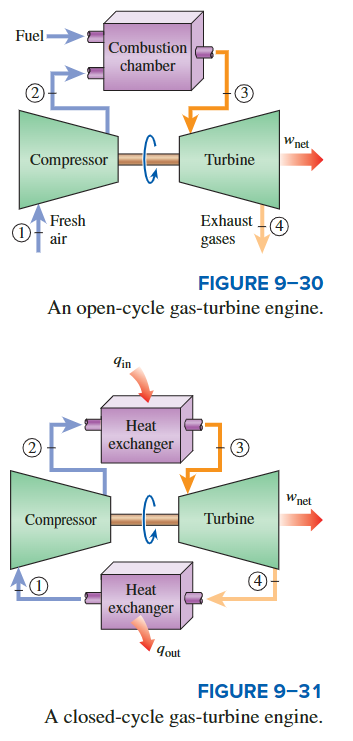
燃气轮机通常在开放循环中运行。

• 环境条件下的新鲜空气被吸入压缩机，在那里其温度和压力升高。
• 高压空气进入燃烧室，在那里燃料在恒定的压力下燃烧。产
• 生的高温气体随后进入涡轮机，在那里它们膨胀到大气压，同时产生动力。
• 离开涡轮机的废气被排出（不再循环），导致循环被归类为开放循环。

通过使用空气标准假设，可以将刚才描述的开放式燃气轮机循环建模为封闭循环。这里，压缩和膨胀过程保持不变，但燃烧过程被来自外部源的恒压加热过程所取代，排气过程被环境空气的恒压排热过程所代替。工作流体在这个闭环中经历的理想循环是布雷顿循环，它由四个内部可逆过程组成

热力学循环

• 等熵压缩 **Isentropic compression** (in a compressor)
• 等压吸热 **Constant-pressure heat addition**
• 等熵膨胀 **Isentropic expansion** (in a turbine)
• 等压放热 **Constant-pressure heat rejection**

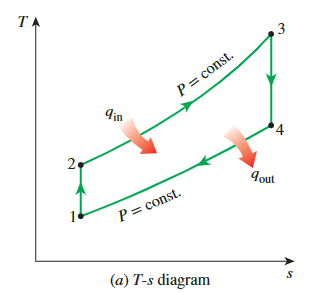
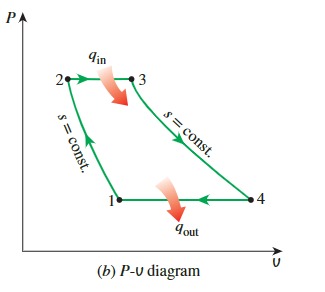
布雷顿循环的所有四个过程都是在稳定流动装置中执行的；因此，它们应该被分析为稳定流动过程。

当动能和势能的变化被忽略时，稳定流动过程的能量平衡可以在单位质量的基础上表示为:

\[ \left(q_{\text {in }}-q_{\text {out }}\right)+\left(w_{\text {in }}-w_{\text {out }}\right)=h_{\text {exit }}-h_{\text {inlet }} \]

在等压过程中：

\[ \begin{aligned}&q_{\text {in }}=h_3-h_2=c_p\left(T_3-T_2\right)\\&q_{\text {out }}=h_4-h_1=c_p\left(T_4-T_1\right)\end{aligned} \]

进一步得到理想布雷顿循环中的热机效率：

\[ \eta_{\text {th,Brayton }}=\frac{w_{\text {net }}}{q_{\text {in }}}=1-\frac{q_{\text {out }}}{q_{\text {in }}}=1-\frac{c_p\left(T_4-T_1\right)}{c_p\left(T_3-T_1\right)}=1-\frac{T_1\left(T_4 / T_1-1\right)}{T_2\left(T_3 / T_2-1\right)} \]

在两个等熵过程中：

\[ \frac{T_2}{T_1}=\left(\frac{P_2}{P_1}\right)^{(k-1) / k}=\left(\frac{P_3}{P_4}\right)^{(k-1) / k}=\frac{T_3}{T_4} \]

代入这些方程：

\[ \eta_{\text {th,Brayton }}=1-\frac{1}{r_p^{(k-1) / k}},\quad r_p=\frac{P_2}{P_1} \]

• 其中\(r_p\)被称为压力比pressure ratio

后工作比率 back work rate

\[ r_{\mathrm{bw}}=\frac{w_{\text {comp,in }}}{w_{\text {turb,out }}} \]

提高热效率

在冷气标准假设下，理想布雷顿循环的热效率取决于燃气轮机的压力比和工作流体的比热比。这两个参数的增加都能提高热效率.

• 提高涡轮进口（或燃烧）温度
• 提高涡轮机械组件的效率
• 对基本周期进行修改

例子

\(P_{501}\)

实际燃气轮机循环与理想循环的偏差

实际的燃气轮机循环在几个方面与理想的布雷顿循环不同。首先，在热添加和热排放过程中会有一些压力下降是不可避免的。更重要的是，由于不可逆性，压缩机的实际输入功更多，而涡轮的实际输出功更少。实际压缩机和涡轮行为与理想的等熵行为的偏差可以通过利用涡轮和压缩机的等熵效率准确地加以考虑

\[ \begin{aligned}&\eta_C=\frac{w_s}{w_a} \cong \frac{h_{2 s}-h_1}{h_{2 a}-h_1}\\&\eta_T=\frac{w_a}{w_s} \cong \frac{h_3-h_{4 a}}{h_3-h_{4 s}}\end{aligned} \]

参考\(P_{502}\)

带再生的布雷顿循环

The Brayton Cycle With Regeneration

基本构成

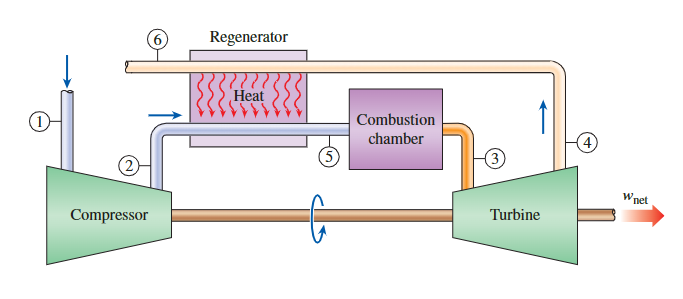
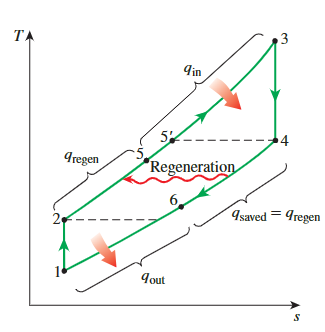
在燃气涡轮发动机中，离开涡轮的排气温度经常比离开压缩机的空气温度高得多。因此，离开压缩机的高压空气可以通过与热排气进行对流热交换来加热，这也被称为再生器或热回收器。 由于再生作用，布雷顿循环的热效率提高了，因为通常向环境散去的废气能量现在被用来预热进入燃烧室的空气。

• 在再生器内部出现的最高温度是T4，是涡轮机排出废气并进入再生器的温度。
• 在任何情况下，空气都不能在再生器内加热到超过这个数值的温度。空气通常以更低的温度T5离开再生器。
• 在极限（理想）情况下，空气以排气气体T4的入口温度离开再生器。

\[ q_{\text {regen,act }}=h_5-h_2 \]

• 假设再生器绝缘良好，并且动能和势能的任何变化都可以忽略不计，排气气体对空气的实际和最大热传递可以表示为

\[ q_{\text {regen, } \max }=h_{5^{\prime}}-h_2=h_4-h_2 \]

• 再生器接近理想再生器的程度称为有效性

\[ \epsilon=\frac{q_{\text {regen,act }}}{q_{\text {regen,max }}}=\frac{h_5-h_2}{h_4-h_2} \]

• 应用冷空气假设**cold-air-standard assumption**

\[ \epsilon \cong \frac{T_5-T_2}{T_4-T_2} \]

热力学效率

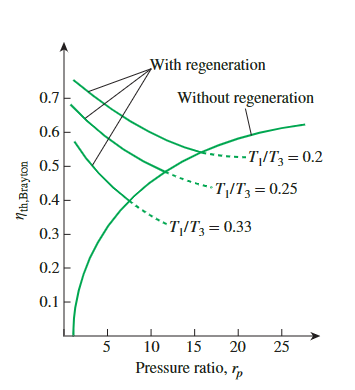
• 理想的热力学效率为：

\[ \eta_{\text {th,regen }}=1-\left(\frac{T_1}{T_3}\right)\left(r_p\right)^{(k-1) / k} \]

示例

参考\(P_{505}\)

具有中间冷却、再加热和再生功能的布雷顿循环

发动机构成

燃气轮机循环的净功是涡轮机输出功与压缩机功输入之间的差值，它可以通过减少压缩机功或增加涡轮机功来增加，或者两者兼而有之。

• 在两个特定压力之间压缩气体所需的功可以通过分阶段进行压缩过程并冷却其间的气体来减少，即使用带中间冷却的多级压缩。随着级数的增加，压缩过程在压缩机入口温度下变得几乎等温，压缩功减小
• 同样，在两个压力水平之间运行的涡轮机的功输出可以通过分阶段膨胀气体并在其间重新加热来增加——也就是说，利用多级膨胀和重新加热。这是在不提高循环中的最高温度的情况下实现的。
• 燃气轮机中的燃烧通常是完全燃烧所需空气量的四倍，以避免过高的温度。因此，废气富含氧气，只需在两种膨胀状态之间向废气中喷射额外的燃料即可实现再加热

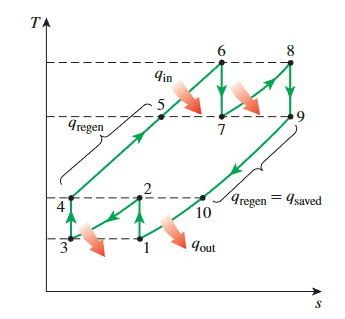
• 如第7章所示，当各级压力比保持相等时，两级压缩机的功输入最小

\[ \frac{P_2}{P_1}=\frac{P_4}{P_3} \text { and } \frac{P_6}{P_7}=\frac{P_8}{P_9} \]

示例

参见\(P_{508}\)

理想喷射脉冲循环

发动机构成

• 理想的喷气推进循环与简单的理想布雷顿循环的不同之处在于，气体在涡轮机中不会膨胀到环境压力。相反，它们被膨胀到一定的压力，使得涡轮机产生的功率刚好足以驱动压缩机和辅助设备，如小型发电机和液压泵。
• 也就是说，喷气推进循环的净功输出为零。
• 飞机燃气轮机在更高的压力比下运行（通常在10到25之间），流体首先通过扩散器，在进入压缩机之前，流体在扩散器中减速并增加压力。

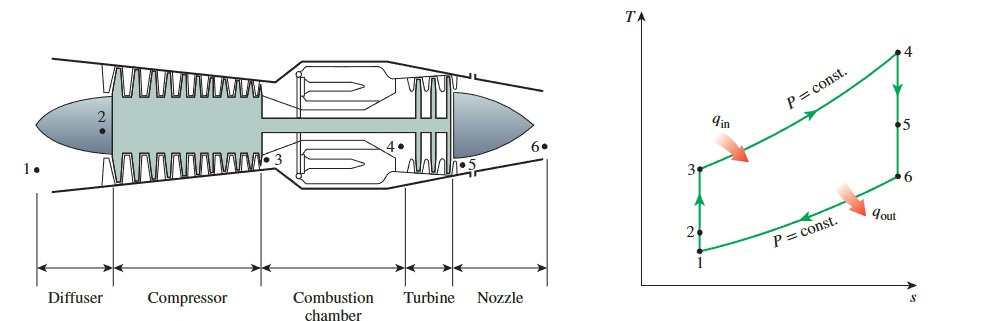
原理分析

• 根据牛顿第二定律，飞行产生的静推力：

\[ F=(\dot{m} V)_{\text {exit }}-(\dot{m} V)_{\text {inlet }}=\dot{m}\left(V_{\text {exit }}-V_{\text {inlet }}\right) \]

• 发动机推力产生的功率称为推进功率：

\[ \dot{W}_P=F V_{\text {aircraft }}=\dot{m}\left(V_{\text {exit }}-V_{\text {inlet }}\right) V_{\text {aircraft }} \quad(\mathrm{kW}) \]

• 热力效率

\[ \eta_P=\frac{\text { Propulsive power }}{\text { Energy input rate }}=\frac{\dot{W}_P}{\dot{Q}_{\text {in }}} \]

示例

参照\(P_{512}\)

燃气动力循环的第二定律分析

理想的卡诺循环，斯特林和埃里克森循环是完全可逆的，但奥托循环，柴油循环和布雷顿循环仅是内部可逆的而不是完全可逆的。

根据第八章，封闭系统的㶲**exergy**和火无**exergy destruction**可被定义为：

\[ \begin{aligned} X_{\text {dest }} & =T_0 S_{\text {gen }}=T_0\left(\Delta S_{\text {sys }}-S_{\text {in }}+S_{\text {out }}\right) \\ & =T_0\left[\left(S_2-S_1\right)_{\text {sys }}-\frac{Q_{\text {in }}}{T_{b, \text { in }}}+\frac{Q_{\text {out }}}{T_{b, \text { out }}}\right] \end{aligned} \]

使用速率形式表示：

\[ \dot{X}_{\text {dest }}=T_0 \dot{S}_{\text {gen }}=T_0\left(\dot{S}_{\text {out }}-\dot{S}_{\text {in }}\right)=T_0\left(\sum_{\text {out }} \dot{m} s-\sum_{\text {in }} \dot{m} s-\frac{\dot{Q}_{\text {in }}}{T_{b, \text { in }}}+\frac{\dot{Q}_{\text {out }}}{T_{b, \text { out }}}\right) \quad(\mathrm{kW}) \]

或者使用单位质量表示：

\[ x_{\text {dest }}=T_0 s_{\text {gen }}=T_0\left(s_e-s_i-\frac{q_{\text {in }}}{T_{b, \text { in }}}+\frac{q_{\text {out }}}{T_{b, \text { out }}}\right) \quad(\mathrm{kJ} / \mathrm{kg}) \]

考虑到循环中，所有的状态量：

\[ x_{\text {dest }}=T_0\left(\frac{q_{\text {out }}}{T_L}-\frac{q_{\text {in }}}{T_H}\right) \quad(\mathrm{kJ} / \mathrm{kg}) \]

由此，在封闭系统和流动系统的㶲被定义为：\(\phi\)和\(\psi\)

\[ \begin{aligned}&\phi=\left(u-u_0\right)-T_0\left(s-s_0\right)+P_0\left(U-U_0\right)+\frac{V^2}{2}+g z&(\mathrm{kJ} / \mathrm{kg})\\&\psi=\left(h-h_0\right)-T_0\left(s-s_0\right)+\frac{V^2}{2}+g z \quad&(\mathrm{~kJ} / \mathrm{kg})\end{aligned} \]

使用热力学第二定律分析奥托系统

\(P_{517}\)