第11章 制冷循环 Refrigeration Cycles
第11章 制冷循环 Refrigeration Cycles
最常用的制冷循环是蒸汽压缩制冷循环
**vapor-compression refrigeration cycle**,其中制冷剂交替汽化和冷凝,并在汽相中被压缩。另一种众所周知的制冷循环是气体制冷循环**gas refrigeration cycle**,其中制冷剂始终保持气相。其他制冷循环包括复叠制冷**cascade refrigeration**(使用多个制冷循环)和吸收式制冷**absorption refrigeration**(制冷剂在压缩前溶解在液体中)
冰箱**Refrigerator**和热泵**heat pump**
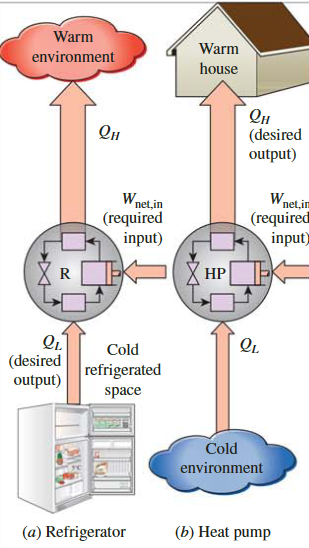
冰箱和热泵本质上是相同的设备;他们仅在目标上有所不同。冰箱的目的是通过去除冷藏空间中的热量来保持冷藏空间的低温。热泵的目的是将加热空间维持在高温。
性能系数
冷机的效率由性能系数
**coefficient of performance**定义:
\[ \begin{gathered}\mathrm{COP}_{\mathrm{R}}=\frac{\text { Desired output }}{\text { Required input }}=\frac{\text { Cooling effect }}{\text { Work input }}=\frac{Q_L}{W_{\text {net,in }}} \\\mathrm{COP}_{\mathrm{HP}}=\frac{\text { Desired output }}{\text { Required input }}=\frac{\text { Heating effect }}{\text { Work input }}=\frac{Q_H}{W_{\text {net,in }}}\end{gathered} \]
- 由于冰箱和热泵本质上的相同,有:\(\mathrm{COP}_{\mathrm{HP}}=\mathrm{COP}_{\mathrm{R}}+1\)
- 热泵最坏的情况充当电阻加热器
- 制冷系统的制冷能力
**cooling capacity**被定义为热量从低温区的抽取速度,并用制冷吨数**tons of refrigeration**表示,具体来说,1 ton代表24h内,在0℃,将1吨水转换为1吨冰。- \(1 ton = 221 kJ/min\)
逆卡诺循环
如同之前讨论过的循环方式,逆卡诺循环也是在制冷中效率最高的循环方式。
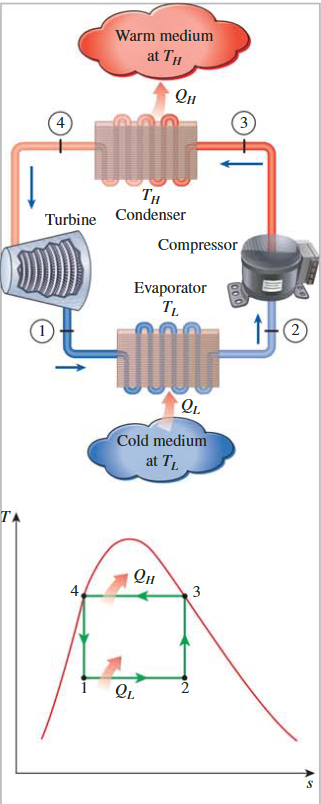
循环过程
- 制冷剂在 \(T_L\)处等温地从低温源吸收 \(Q_L\) 量的热量(过程 1-2)
- 被等熵压缩至状态 3(温度升至 \(T_H\))
- 在 \(T_L\) 处等温地将热量排出至高温散热器。 排出热量为 \(Q_H\)(过程 3-4)。制冷剂在冷凝器中从饱和蒸气状态变为饱和液体状态
- 等熵膨胀至状态 1(温度降至 \(T_L\))
性能系数
\[ \begin{aligned}&\mathrm{COP}_{\mathrm{R}, \text { Carnot }}=\frac{1}{T_H / T_L-1}\\&\mathrm{COP}_{\mathrm{HP}, \mathrm{Carnot}}=\frac{1}{1-T_L / T_H}\end{aligned} \]
- 同样的,两个等温过程很难实现,因此逆卡诺循环并不是制冷循环的合理模型
理想的蒸汽压缩制冷循环
通过在压缩制冷剂之前完全蒸发制冷剂以及用节流
**throttling**装置(例如膨胀阀或毛细管)替换涡轮机,可以消除与逆卡诺循环相关的许多不切实际的问题。由此产生的循环称为理想蒸汽压缩制冷循环**Ideal vapor-compression refrigeration cycle**
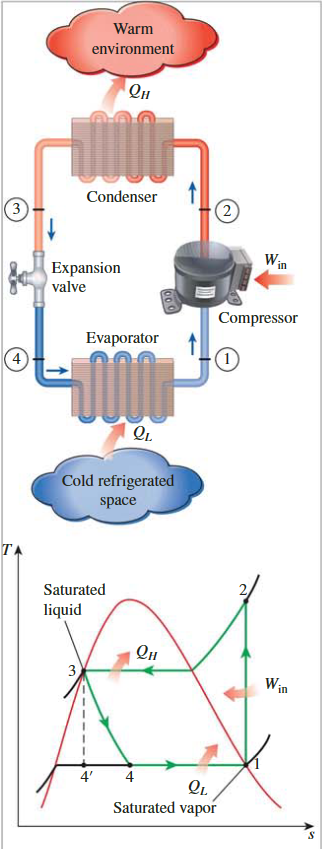
循环构成
一如既往,它由四个过程组成
- 1-2 压缩机中的等熵压缩
- 制冷剂以饱和蒸气状态进入压缩机,并被等熵压缩至冷凝器压力。
- 制冷剂的温度升高至远高于周围介质的温度。
- 2-3 冷凝器中的恒压排热
- 制冷剂以状态 2 的过热蒸汽形式进入冷凝器
- 向周围环境散热而以状态 3 的饱和液体形式离开
- 此状态下制冷剂的温度仍高于周围环境的温度
- 3-4 膨胀装置中的节流
- 状态 3 的饱和液态制冷剂通过膨胀阀或毛细管节流至蒸发器压力
- 制冷剂的温度降至冷藏空间的温度以下
- 4-1 蒸发器中的恒压吸热
- 制冷剂以状态4作为低质量饱和混合物进入蒸发器,并通过吸收冷藏空间的热量而完全蒸发。
- 制冷剂以饱和蒸气形式离开蒸发器
- 根据经验,蒸发温度每升高1 ℃ 或冷凝温度每降低1 ℃,COP 就会提高 2% 到 4%。
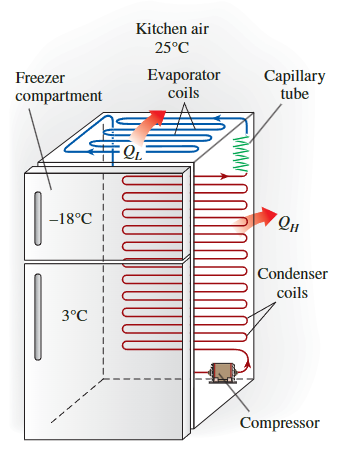
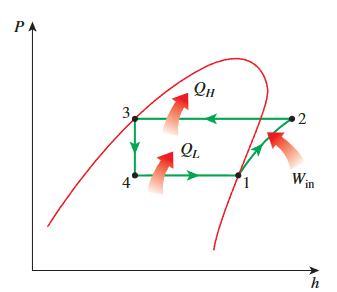
- 理想的蒸汽压缩制冷不是内部可逆的,其中的节流过程不可逆
能量分析
稳流,忽略动能势能变化
\[ \left(q_{\text {in }}-q_{\text {out }}\right)+\left(w_{\text {in }}-w_{\text {out }}\right)=h_e-h_i \]
- 系统中只有近似绝热的压缩机做功
\[ \begin{aligned}&\mathrm{COP}_{\mathrm{R}}=\frac{q_L}{w_{\text {net, in }}}=\frac{h_1-h_4}{h_2-h_1}&\mathrm{COP}_{\mathrm{HP}}=\frac{q_H}{w_{\text {net,in }}}=\frac{h_2-h_3}{h_2-h_1}\end{aligned} \]
- 其中\(h_1=h_{g @ P_1} \text { and } h_3=h_{f @ P_3}\)
例子
P_602
实际蒸汽压缩制冷循环
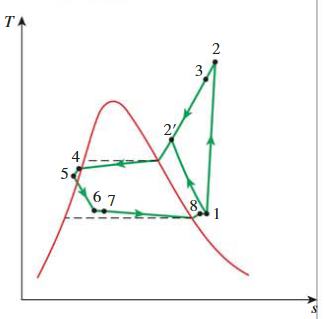
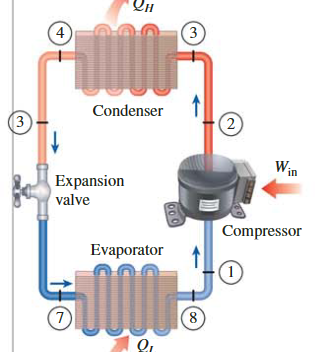
- 在实际过程中,不可能精准的控制制冷器的状态
- 因此使制冷剂在压缩机入口稍微过热以保证完全气化
- 这要求压缩机的功率增加
- 同样的,制冷剂在进入节流阀之前会稍稍过冷
- 由于会增加熵的摩擦过程和会减少熵的传热过程,制冷剂的熵会在压缩过程中增加(过程1-2)或者减少(过程1-2'),我们更倾向于使用过程(过程1-2')
例子
P_603
蒸汽压缩制冷循环的热力学第二定律分析
火用分析
\[ \dot{X}_{\text {dest }}=T_0 \dot{S}_{\text {gen }} \]
其中,对于冰箱,\(T_0\)通常是高温介质的温度\(T_H\)(对于热泵来说是\(T_L\))
对于压缩机:
\[ \dot{X}_{\text {dest }, 1-2}=T_0 \dot{S}_{\text {gen, } 1-2}=\dot{m} T_0\left(s_2-s_1\right) \]
\[ \begin{aligned}\eta_{\mathrm{II}, \text { Comp }} & =\frac{\dot{X}_{\text {recovered }}}{\dot{X}_{\text {expended }}}=\frac{\dot{W}_{\text {rev }}}{\dot{W}_{\text {act,in }}}=\frac{\dot{m}\left[h_2-h_1-T_0\left(s_2-s_1\right)\right]}{\dot{m}\left(h_2-h_1\right)}=\frac{\psi_2-\psi_1}{h_2-h_1} \\& =1-\frac{\dot{X}_{\text {dest, }, 1-2}}{\dot{W}_{\text {act,in }}}\end{aligned} \]
对于制冷机:
\[ \dot{X}_{\text {dest }, 2-3}=T_0 \dot{S}_{\text {gen }, 2-3}=T_0\left[\dot{m}\left(s_3-s_2\right)+\frac{\dot{Q}_H}{T_H}\right] \]
\[ \begin{aligned}\eta_{\mathrm{II}, \text { Cond }} & =\frac{\dot{X}_{\text {recovered }}}{\dot{X}_{\text {expended }}}=\frac{\dot{X}_{Q_{I I}}}{\dot{X}_2-\dot{X}_3}=\frac{\dot{Q}_H\left(1-T_0 / T_H\right)}{\dot{X}_2-\dot{X}_3} \\& =\frac{\dot{Q}_H\left(1-T_0 / T_H\right)}{\dot{m}\left[h_2-h_3-T_0\left(s_2-s_3\right)\right]}=1-\frac{\dot{X}_{\text {dest }, 2-3}}{\dot{X}_2-\dot{X}_3}\end{aligned} \]
- 请注意,当 \(T_H = T_0\)(通常是冰箱的情况)时,\(\eta_{\mathrm{II}, \text { Cond }} = 0,\)因为在这种情况下没有可恢复的火用
对于扩张机:
\[ \begin{gathered} \dot{X}_{\text {dest,3-4 }}=T_0 \dot{S}_{\text {gen,3-4 }}=\dot{m} T_0\left(s_4-s_3\right) \\ \eta_{\text {II,ExpValve }}=\frac{\dot{X}_{\text {recovered }}}{\dot{X}_{\text {expended }}}=\frac{0}{\dot{X}_3-\dot{X}_4}=0 \end{gathered} \]
or
\[ \eta_{\text {II,ExpValve }}=1-\frac{\dot{X}{\text {dest, } 3-4}}{\dot{X}{\text {expended }}}=1-\frac{\dot{X}_3-\dot{X}_4}{\dot{X}_3-\dot{X}_4}=0 \]
对于蒸发器
\[ \begin{gathered} \dot{X}_{\text {dest,4-1 }}=T_0 \dot{S}_{\text {gen }, 4-1}=T_0\left[\dot{m}\left(s_1-s_4\right)-\frac{\dot{Q}_L}{T_L}\right] \\ \eta_{\text {II,Evap }}=\frac{\dot{X}_{\text {recovered }}}{\dot{X}_{\text {expended }}}=\frac{\dot{X}_{\dot{Q}_L}}{\dot{X}_4-\dot{X}_1}=\frac{\dot{Q}_L\left(T_0-T_L\right) / T_L}{\dot{X}_4-\dot{X}_1} \\ =\frac{\dot{Q}_L\left(T_0-T_L\right) / T_L}{\dot{m}\left[h_4-h_1-T_0\left(s_4-s_1\right)\right]}=1-\frac{\dot{X}_{\text {dest }, 4-1}}{\dot{X}_4-\dot{X}_1} \end{gathered} \]
我们使用\(\dot{X}_{\dot{Q}_L}\)表示火用率的正值
\[ \dot{X}_{\dot{Q}_L}=\dot{Q}_L \frac{T_0-T_L}{T_L} \]
总的火用值
\[ \dot{X}_{\text {dest,total }}=\dot{X}_{\text {dest,1-2 }}+\dot{X}_{\text {dest, } 2-3}+\dot{X}_{\text {dest, } 3-4}+\dot{X}_{\text {dest,4-1 }} \]
\[ \dot{X}_{\text {dest,total }}=\dot{W}_{\text {in }}-\dot{X}_{\dot{Q}_L} \]
\[ \eta_{\mathrm{II}, \text { cycle }}=\frac{\dot{X}_{\dot{Q}_L}}{\dot{W}_{\text {in }}}=\frac{\dot{W}_{\text {min,in }}}{\dot{W}_{\text {in }}}=1-\frac{\dot{X}_{\text {dest,total }}}{\dot{W}_{\text {in }}} \]
考虑到\(\dot{W}_{\text {in }}=\frac{\dot{Q}_L}{\mathrm{COP}_{\mathrm{R}}} \quad \text { and } \quad \dot{X}_{\dot{Q}_L}=\dot{Q}_L \frac{T_0-T_L}{T_L}\)
\[ \eta_{\text {II,cycle }}=\frac{\dot{X}_{\dot{Q}_L}}{\dot{W}_{\text {in }}}=\frac{\dot{Q}_L\left(T_0-T_L\right) / T_L}{\dot{Q}_L / \mathrm{COP}_{\mathrm{R}}}=\frac{\mathrm{COP}_{\mathrm{R}}}{T_L /\left(T_H-T_L\right)}=\frac{\mathrm{COP}_{\mathrm{R}}}{\mathrm{COP}_{\mathrm{R}, \mathrm{rev}}} \]
- 其中:
\[ \mathrm{COP}_{\mathrm{R}, \text { rev }}=\mathrm{COP}_{\mathrm{R}, \text { Carnot }}=\frac{T_L}{T_H-T_L}=\frac{1}{T_H / T_L-1} \]
例子
P_607
选择正确的制冷剂
- 制冷剂的选择取决于多种因素,包括其对臭氧层的影响、成本、热力学性能以及安全性等。
- 常见的制冷剂包括CFCs、HFCs、HCFCs、氨、烃类,以及二氧化碳等。
- 例如,氨是一种优秀的制冷剂,尽管其有毒性,但其低成本、高COPs、优良的热力学和传热性能使其在食品制冷设施等领域得到了广泛的应用。
- CFCs曾被广泛应用,但由于其对臭氧层的破坏,现在已经被禁止或限制使用。目前,新型的、对臭氧层友好的制冷剂(如R-134a等)正在逐步替代传统制冷剂。
- 此外,当单一制冷剂无法满足温度要求时,可以使用两个或更多的制冷循环进行串联,即级联制冷系统。制冷剂的其他理想特性包括无毒、无腐蚀性、不易燃烧、化学稳定性好,且具有高的汽化热,当然,低成本也是一个重要的考虑因素。
热泵系统
- 热泵系统的初始购买和安装成本通常比其他加热系统更高
- 但在某些地区,由于它们能降低供暖费用,因此从长远来看可以节省资金。
- 热泵最常见的能源是大气空气(空气对空气系统),尽管水和土壤也被使用。热泵的COP通常在1.5和4之间变化,具体取决于使用的特定系统和源的温度。
- 新类别的最近开发的热泵使用变速电动机驱动器,其能效至少是其前身的两倍。
- 然而,热泵的能力和效率在低温下会显著降低,因此,大多数空气源热泵需要辅助加热系统,如电阻加热器或油炉或燃气炉。
- 最后,热泵和空调具有相同的机械组件,因此,为满足建筑物的供暖和制冷需求,拥有两套独立的系统是不经济的。一个系统可以在冬天用作热泵,在夏天用作空调。
创新的蒸汽压缩制冷系统
复叠制冷系统
**Cascade Refrigeration Systems**
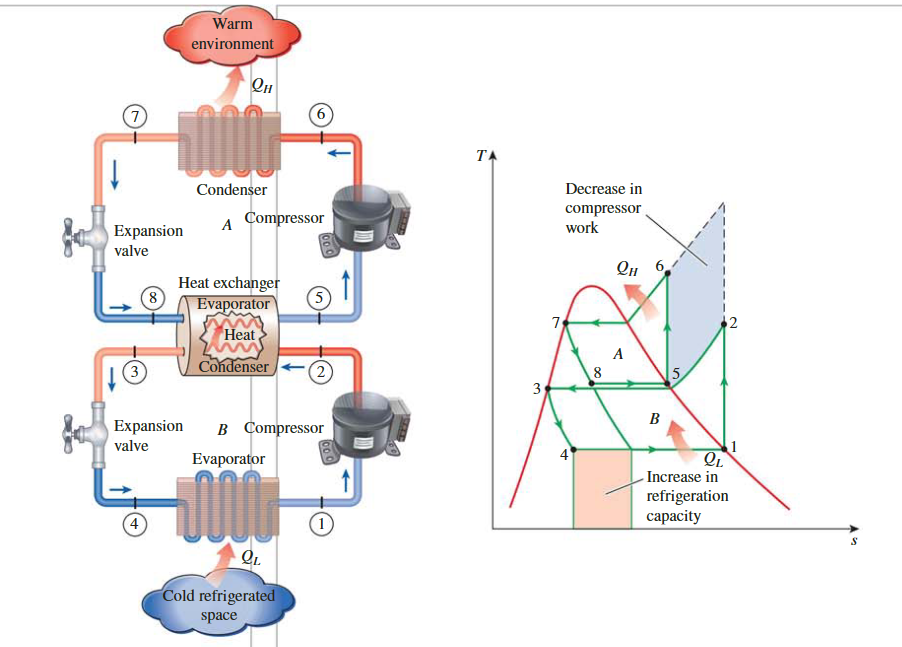
\[ \begin{gathered}\dot{m}_A\left(h_5-h_8\right)=\dot{m}_B\left(h_2-h_3\right) \longrightarrow \frac{\dot{m}_A}{\dot{m}_B}=\frac{h_2-h_3}{h_5-h_8} \\\mathrm{COP}_{\mathrm{R}, \text { cascade }}=\frac{\dot{Q}_L}{\dot{W}_{\text {net, in }}}=\frac{\dot{m}_B\left(h_1-h_4\right)}{\dot{m}_A\left(h_6-h_5\right)+\dot{m}_B\left(h_2-h_1\right)}\end{gathered} \]
例子
P_614
多级压缩制冷系统Multistage Compression Refrigeration Systems
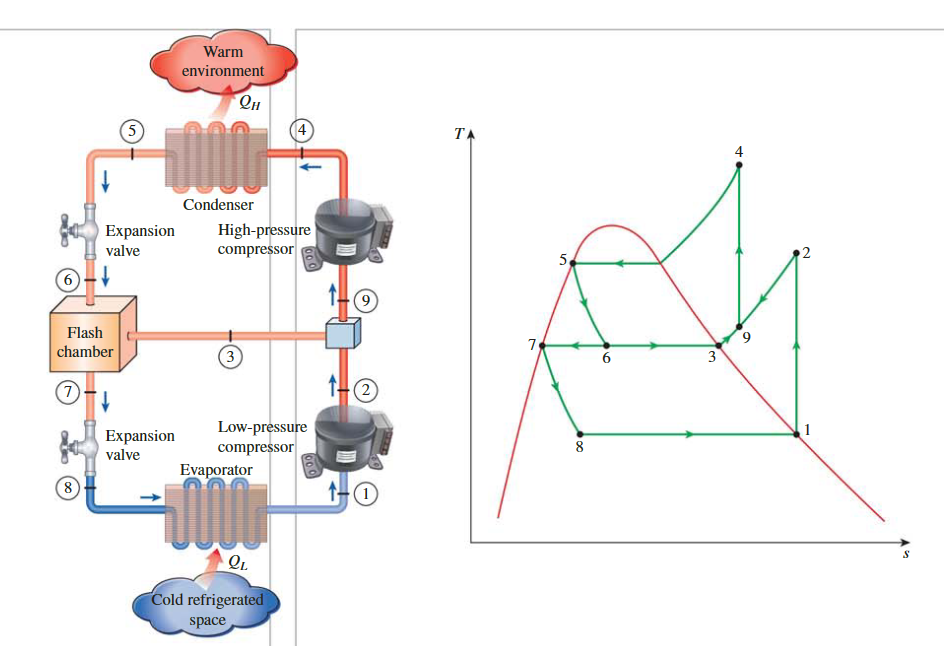
例子
P_616
配备单个压缩机的多用途制冷系统
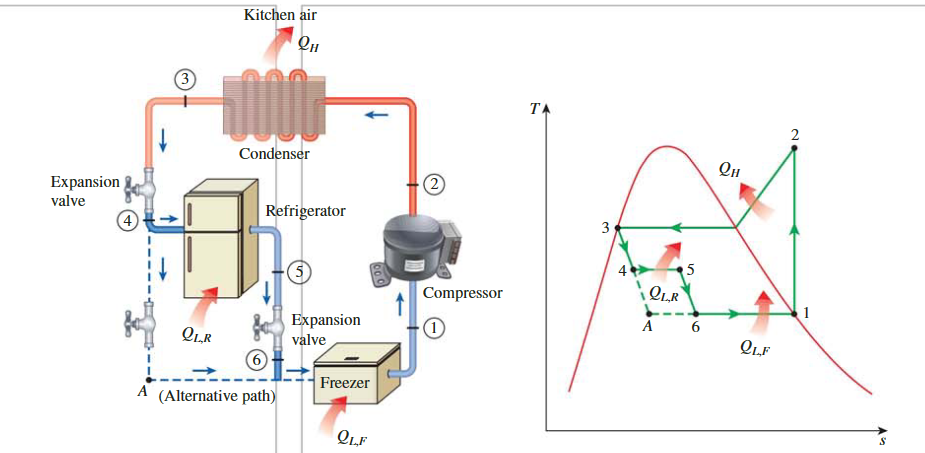
气体液化
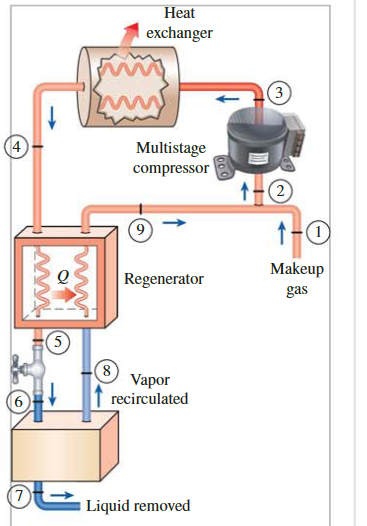
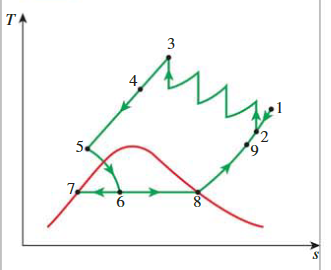
液化气体在制冷领域有重要应用,用于诸如从空气中分离氮氧,制备火箭推进剂,研究低温材料性能和超导性等科学和工程过程。常用的液化气体,如氦、氢、氮在大气条件下无法存在为液态,因此需通过特定的循环技术例如Linde-Hampson循环来达到液化。此类循环涉及多个步骤,包括压缩、冷却和节流。此外,这些制冷循环也可用于气体的固化。
气体制冷循环
**gas refrigeration cycle**
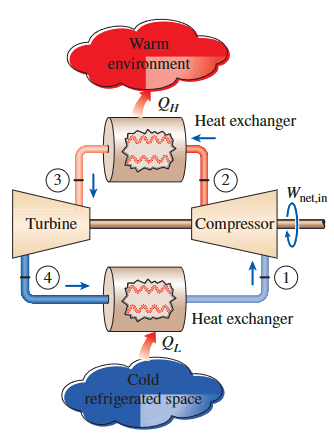
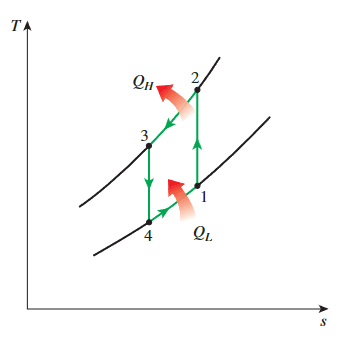
\[ \begin{gathered}\mathrm{COP}_{\mathrm{R}}=\frac{q_L}{w_{\text {net,in }}}=\frac{q_L}{w_{\text {comp,in }}-w_{\text {turb,out }}} \\q_L=h_1-h_4 \\w_{\text {turb,out }}=h_3-h_4 \\w_{\text {comp,in }}=h_2-h_1\end{gathered} \]
带再生的气体制冷循环
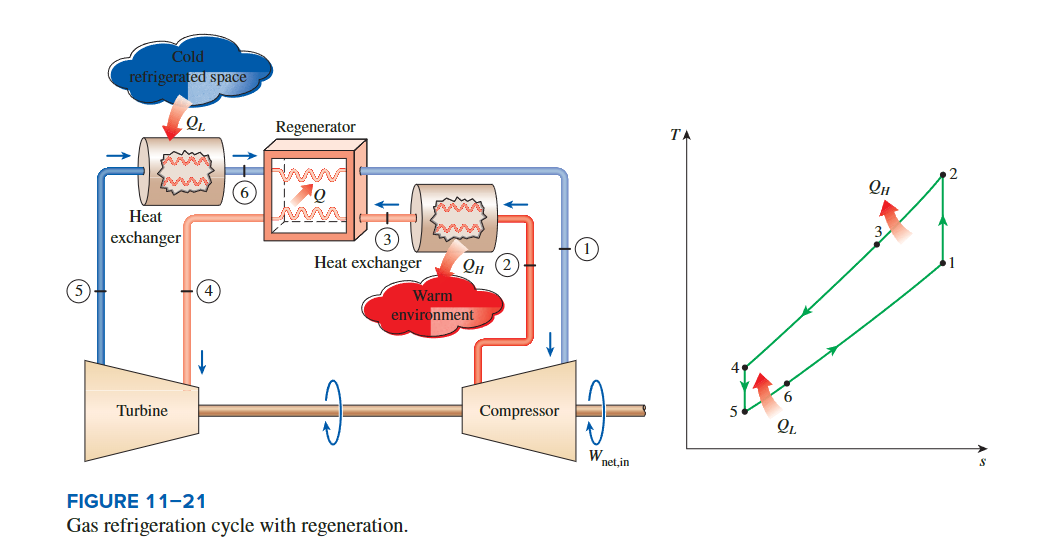
例子
P_621
吸收式制冷系统
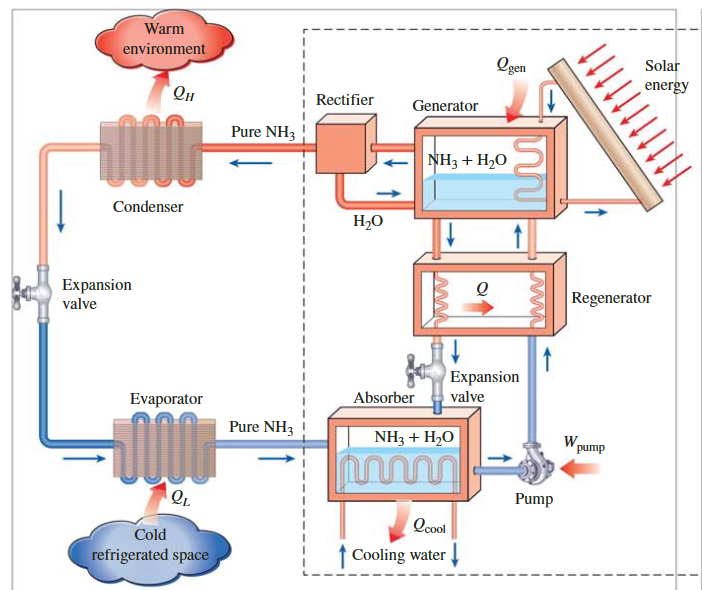
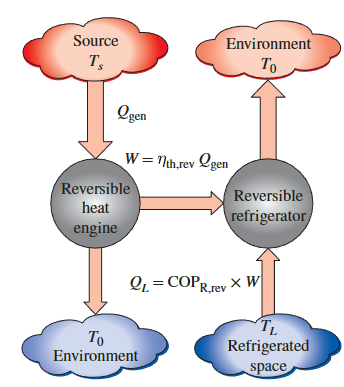
\[ \mathrm{COP}_{\text {absorption }}=\frac{\text { Desired output }}{\text { Required input }}=\frac{Q_L}{Q_{\text {gen }}+W_{\text {pump }}} \cong \frac{Q_L}{Q_{\text {gen }}} \]
\[ \mathrm{COP}_{\text {rev,absorption }}=\frac{Q_L}{Q_{\text {gen }}}=\eta_{\text {th,rev }} \operatorname{COP}_{\mathrm{R}, \text { rev }}=\left(1-\frac{T_0}{T_s}\right)\left(\frac{T_L}{T_0-T_L}\right) \]
例子
P_625
SUMMARY
制冷是将热量从低温区域转移到高温区域的过程。实现制冷的设备被称为冰箱,它们运行的循环被称为制冷循环。
冰箱用于通过从较冷的介质中传热以加热空间被称为热泵。
冰箱和热泵的性能用性能系数(COP)来表达,它定义为期望的输出除以所需的输入。
\[ \begin{aligned}& \mathrm{COP}_{\mathrm{R}}=\frac{\text { Desired output }}{\text { Required output }}=\frac{\text { Cooling effect }}{\text { Work input }}=\frac{Q_{\mathrm{L}}}{W_{\text {net,in }}} \\& \mathrm{COP}_{\mathrm{HP}}=\frac{\text { Desired output }}{\text { Required output }}=\frac{\text { Heating effect }}{\text { Work input }}=\frac{Q_H}{W_{\text {net,in }}}\end{aligned} \]
逆卡诺循环是制冷循环的比较标准。运行在逆卡诺循环上的冰箱或热泵被称为卡诺冰箱或卡诺热泵,它们的COP公式给出。
\[ \begin{aligned}\mathrm{COP}_{\mathrm{R}, \text { Carnot }} & =\frac{1}{T_H / T_L-1} \\\mathrm{COP}_{\mathrm{HP}, \text { Carnot }} & =\frac{1}{1-T_L / T_H}\end{aligned} \]
最广泛使用的制冷循环是蒸汽压缩制冷循环。在理想的蒸汽压缩制冷循环中,制冷剂以饱和蒸汽的状态进入压缩机,并在冷凝器中被冷却为饱和液态。
通过串联操作两个或更多的蒸汽压缩系统,可以达到非常低的温度,这被称为级联。级联的结果是提高了制冷系统的COP。
动力循环通过简单地反转可以用作制冷循环。其中,反布莱顿循环(也称为气体制冷循环)用于冷却飞机和获得非常低的(低温)温度。
\[ \mathrm{COP}_{\mathrm{R}}=\frac{q_L}{w_{\text {net,in }}}=\frac{q_L}{w_{\text {comp,in }}-w_{\text {turb,out }}} \]
当有100到200°C的热源可用时,吸收式制冷变得经济吸引力。在吸收制冷中,制冷剂被输送介质吸收并以液态压缩。吸收制冷系统的COP定义为期望的输出除以所需的输出。
\[ \mathrm{COP}_{\text {absorption }}=\frac{\text { Desired output }}{\text { Required output }}=\frac{Q_L}{Q_{\text {gen }}+W_{\text {pump }}} \cong \frac{Q_L}{Q_{\text {gen }}} \]
\[ \mathrm{COP}_{\text {rev,absorption }}=\eta_{\text {th,rev }} \mathrm{COP}_{\mathrm{R}, \text { rev }}=\left(1-\frac{T_0}{T_s}\right)\left(\frac{T_L}{T_0-T_L}\right) \]



