DCGAN
DCGAN
Created: November 22, 2023 3:27 PM Class: 第七学期 Type: Quick Study Reviewed: No Status: Not started
本文参考pyTorch的相应教程快速实践生成式对抗神经网络
DCGAN Tutorial — PyTorch Tutorials 2.1.1+cu121 documentation
尝试实现的代码可以在以下链接找到,实际上与原文提供的代码基本完全相同:
GitHub - RaphaelHyaan/GAN_etude: 学习使用GAN网络
本文很多内容是对此文章的拙略翻译
简介
本教程将通过一个例子介绍DCGANs。我们将训练一个生成对抗网络(GAN)来生成新的名人,前提是向它展示了许多真实名人的照片。这里的大部分代码来自于pytorch/examples中的DCGAN实现,本文将详细解释实现,并阐明这个模型如何以及为什么工作。但是,不用担心,无需事先了解GANs,但是初学者可能需要花一些时间来推理实际上在底层发生了什么。另外,为了节省时间,最好有一个或两个GPU。让我们从头开始。
生成对抗网络
什么是GAN?
- GANs是一个框架,用于教授深度学习模型如何捕获训练数据分布,以便我们可以从同一分布中生成新数据。GANs由Ian Goodfellow于2014年发明,并首次在生成对抗网络一文中描述。
- 它们由两个不同的模型组成,一个生成器和一个鉴别器。
- 生成器的任务是生成看起来像训练图像的‘假’图像。
- 鉴别器的任务是查看图像并输出它是否是来自生成器的真实训练图像或假图像。
- 在训练过程中,生成器不断尝试通过生成越来越好的假图像来智胜鉴别器,而鉴别器则努力成为更好的侦探,正确地分类真实和假图像。
- 这个游戏的平衡点是生成器生成的假图像看起来就像直接来自训练数据,而鉴别器则总是以50%的信心猜测生成器的输出是真实还是假的。
符号定义
鉴别器
- 现在,让我们定义一些在整个教程中使用的符号,从鉴别器开始。设\(x\)为表示图像的数据。\(D(x)\)是鉴别器网络,它输出\(x\)来自训练数据而不是生成器的(标量)概率。
- 在这里,由于我们正在处理图像,所以\(D(x)\)的输入是CHW大小3x64x64的图像。
- 直观地说,当\(x\)来自训练数据时,\(D(x)\)应该是
HIGH,当\(x\)来自生成器时,应该是**LOW**。\(D(x)\)也可以被视为传统的二元分类器。
生成器
- 对于生成器的符号,设\(z\)是一个从标准正态分布中采样的潜在空间向量。\(G(z)\)表示生成器函数,它将潜在向量\(z\)映射到数据空间。\(G\)的目标是估计训练数据来自的分布\((p_{data})\),以便它可以从该估计分布(\(P_g\))生成假样本。
因此,\(D(G(z))\)是生成器\(G\)的输出是真实图像的概率(标量)。
如Goodfellow的论文所述,\(D\)和\(G\):
- \(D\)试图最大化正确分类真实和假的概率\((logD(x))\)
- \(G\)试图最小化\(D\)预测其输出是假的概率\((1-log(D(x)))\)
- 从论文中,GAN的损失函数是
\[ min_Gmax_DV(D,G)=E_{x∼pdata(x)}[logD(x)]+E_{z∼pz(z)}[log(1−D(G(z)))] \]
理论上,这个极小极大游戏的解是\(p_g = p_{data}\),并且鉴别器随机猜测输入是真实还是假的。然而,GAN的收敛理论仍在积极研究中,实际上模型并不总是训练到这一点。
什么是DCGAN?
DCGAN是上述GAN的直接扩展,不同之处在于它在鉴别器和生成器中明确使用了卷积和卷积转置层。它首次由Radford等人在论文无监督表示学习与深度卷积生成对抗网络中描述。
- 鉴别器由分步卷积层,批量标准化层,和LeakyReLU激活组成。输入是3x64x64的输入图像,输出是输入来自真实数据分布的标量概率。
- 生成器由卷积转置层,批量标准化层和ReLU激活组成。输入是从标准正态分布中抽取的潜在向量\(z\),输出是3x64x64的RGB图像。分步卷积转置层允许潜在向量被转换为与图像相同形状的体积。
- 在论文中,作者还给出了一些关于如何设置优化器,如何计算损失函数,以及如何初始化模型权重的提示,所有这些将在接下来的部分中解释。
输入
定义一些运行的输入:
dataroot- 数据集文件夹的根路径。我们将在下一节详细讨论数据集。workers- 用于通过DataLoader加载数据的工作线程数。batch_size- 训练中使用的批次大小。DCGAN论文使用的批次大小为128。image_size- 用于训练的图像的空间大小。此实现默认为64x64。如果需要其他大小,必须改变D和G的结构。具体详情请看这里。nc- 输入图像的颜色通道数量。对于彩色图像,这是3。nz- 潜在向量的长度。ngf- 与通过生成器传输的特征图的深度有关。ndf- 设置通过鉴别器传播的特征图的深度。num_epochs- 运行的训练时期数。更长时间的训练可能会导致更好的结果,但也需要更长的时间。lr- 训练的学习率。如DCGAN论文所描述,这个数字应为0.0002。beta1- Adam优化器的beta1超参数。如论文所述,这个数应为0.5。ngpu- 可用的GPU数量。如果这个数为0,代码将在CPU模式下运行。如果这个数大于0,它将在该数量的GPU上运行。
1 | # 参数设置 |
数据
在这个教程中,我们将使用 Celeb-A Faces
数据集,您可以在链接的网站上下载,或者在 Google
Drive 中下载。下载的数据集将以 img_align_celeba.zip
的文件名下载。下载后,创建一个名为 celeba 的目录,并将 zip
文件解压缩到该目录中。然后,将这个笔记本的 dataroot
输入设置为您刚刚创建的 celeba
目录。最终的目录结构应如下:
1 | /path/to/celeba |
这是一个重要的步骤,因为我们将使用 ImageFolder
数据集类,它要求数据集根文件夹中有子目录。现在,我们可以创建数据集,创建数据加载器,设置运行设备,最后可视化一些训练数据。
1 | # 我们可以使用设置好的图像文件夹数据集。 |
显示效果:

实施
设置了输入参数并准备好了数据集后,我们现在可以开始实施了。我们将从权重初始化策略开始,然后详细讨论生成器、鉴别器、损失函数和训练循环。
权重初始化
从DCGAN论文中,作者指定所有模型权重应从均值为0、标准差为0.02的正态分布中随机初始化。weights_init函数接受一个初始化的模型作为输入,并重新初始化所有卷积、卷积转置和批量标准化层以满足这一标准。这个函数在模型初始化后立即应用。
1 | # 自定义权重初始化函数,用于初始化“netG”和“netD” |
生成器
生成器 \(G\) 的设计目的是将潜在空间向量 \((z)\) 映射到数据空间。由于我们的数据是图像,因此将 \(z\) 转换为数据空间意味着最终创建与训练图像相同大小的RGB图像(即
3x64x64)。在实践中,这是通过一系列步距为2的二维卷积转置层来完成的,每个层都配对一个2d批量归一化层和一个relu激活函数。
生成器的输出通过tanh函数进行处理,以将其返回到输入数据范围[−1,1]。
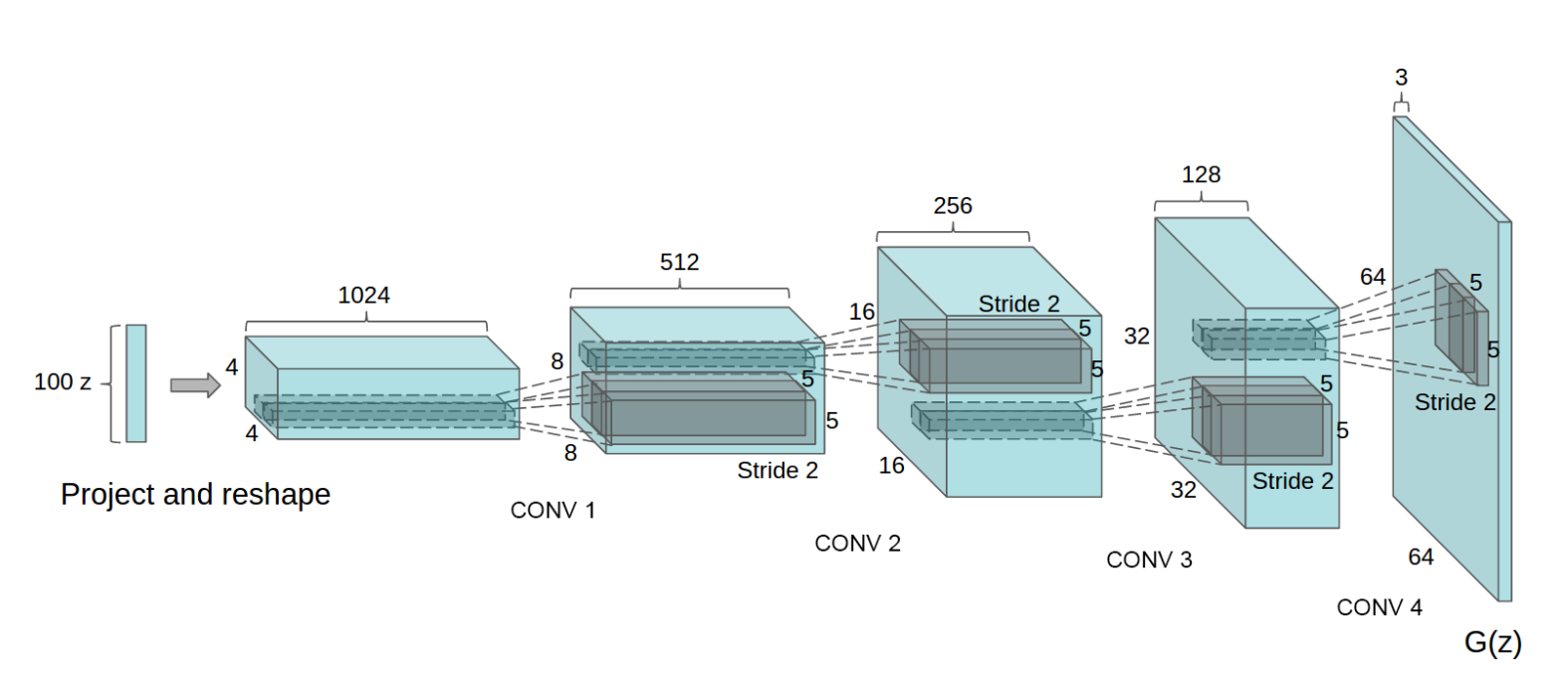
卷积转置层后存在批量归一化函数,这是DCGAN论文的关键贡献。这些层有助于在训练期间梯度的流动。以下是来自DCGAN论文的生成器图像。
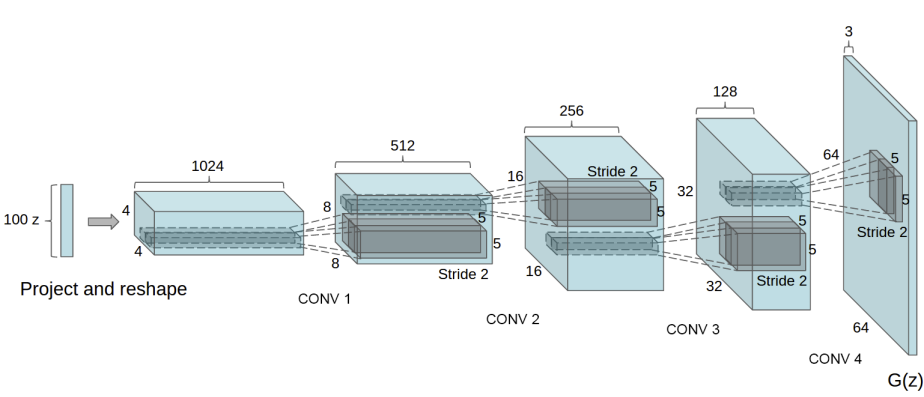
请注意,我们在输入部分设置的输入(nz,ngf和nc)如何在代码中影响生成器架构。nz是z输入向量的长度,ngf与通过生成器传播的特征图的大小有关,而nc是输出图像中的通道数量(设置为3以获取RGB图像)。以下是生成器的代码。
1 | # Generator 代码 |
现在,我们可以实例化生成器并应用 weights_init
函数。查看打印的模型以查看生成器对象的结构。
1 | # 创建生成器 |
鉴别器
如前所述,鉴别器 D 是一个二元分类网络,其输入是一张图片,输出是输入图片为真(相对于假)的概率。在这里,D 接收一张3x64x64的输入图像,通过一系列的 Conv2d, BatchNorm2d, 和 LeakyReLU 层处理它,并通过 Sigmoid 激活函数输出最后的概率。如果问题需要,可以扩展这个体系结构的更多层,但是 strided 卷积,BatchNorm,和 LeakyReLUs 的使用有其重要性。DCGAN 论文提到,使用 strided 卷积而不是池化进行下采样是一种好的实践,因为它让网络学习自己的池化函数。同时,批量标准化和 leaky relu 函数促进了健康的梯度流动,这对于 G 和 D 的学习过程至关重要。
鉴别器代码
1 | class Discriminator(nn.Module): |
现在,和生成器一样,我们可以创建鉴别器,应用
weights_init 函数,并打印模型的结构。
1 | # 创建鉴别器 |
损失函数和优化器
损失函数
有了\(D\)和\(*G*\)的设置,我们可以通过损失函数和优化器来指定他们的学习方式。我们将使用二元交叉熵损失(BCELoss)函数,该函数在PyTorch中定义为:
\[ ℓ(x,y)=L=\{l_1,…,l_N\}^⊤,\ \ \ \ ln=−[y_n⋅logx_n+(1−y_n)⋅log(1−x_n)] \]
- 注意这个函数如何提供目标函数中的两个\(log\)组件的计算(即 \(*log(D(x))*\) 和 \(*log(1−D(G(z)))*\))。我们可以通过 \(*y*\) 输入来指定使用BCE等式的哪一部分。这在即将出现的训练循环中实现,但了解我们如何通过改变 \(*y*\)(即 GT标签)来选择要计算哪个组件是很重要的。
真假标签
接下来,我们定义我们的真实标签为1,假标签为0。这些标签将在计算 \(D\) 和 \(*G*\) 的损失时使用,这也是原始GAN论文中使用的约定。
优化器
最后,我们为 \(*D*\) 和 \(*G*\) 分别设置两个独立的优化器。
- 两者都是\(lr = 0.0002,Beta1 = 0.5\)的Adam优化器。
噪音
为了跟踪生成器的学习进度,我们将生成一批固定的从高斯分布中抽取的潜在向量(即 fixed_noise)。在训练循环中,我们会定期将这个fixed_noise输入到 \(*G*\) 中,随着迭代的进行,我们会看到图像从噪声中形成。
1 | # 初始化 "BCELoss" 函数 |
训练
最后,既然我们已经定义了所有的GAN框架部分,我们可以开始训练它。
- 要注意的是,训练GANs有点抽象,因为不正确的超参数设置会导致模式崩溃,而对于出了什么问题却鲜有解释。
- 在这里,我们将紧密遵循来自Goodfellow的论文的算法1,同时遵守在ganhacks中显示的一些最佳实践。
- 也就是说,我们将“为真实和假图像构造不同的小批量”,并将G的目标函数调整为最大化\(*log(D(G(z)))*\)。训练分为两个主要部分。第1部分更新鉴别器,第2部分更新生成器。
1 | # 训练循环 |
第1部分 - 训练鉴别器
训练鉴别器的目标是最大化正确地将给定输入分类为真实或假的概率。
- 在Goodfellow的角度来看,我们希望“通过提升其随机梯度来更新鉴别器”。
- 实际上,我们希望最大化\(*log(D(x))+log(1−D(G(z)))*\)。
- 由于来自ganhacks的单独小批量建议,我们将分两步计算这个。
- 首先,我们将从训练集中构造一个真实样本的批次,通过\(*D*\)进行前向传播,计算损失(\(*log(D(x))*\)),然后在一个反向传播中计算梯度。
- 其次,我们将使用当前的生成器构造一个假样本的批次,通过\(*D*\)对这个批次进行前向传播,计算损失(\(*log(1−D(G(z)))*\)),并在反向传播中累积梯度。
- 现在,有了来自全部真实和全部假批次的梯度积累,我们调用鉴别器优化器的步骤。
1 | ############################ |
第2部分 - 训练生成器
如原始论文所述,我们希望通过最小化\(*log(1−D(G(z)))*\)来训练生成器,以努力生成更好的假样本。如前所述,Goodfellow证明这并不能提供足够的梯度,特别是在学习过程的早期。
- 作为一种修复方法,我们反而希望最大化\(*log(D(G(z)))*\)。
- 在代码中,我们通过以下方式实现这一点:
- 使用鉴别器对第1部分的生成器输出进行分类
- 使用真实标签作为GT来计算G的损失
- 在反向传播中计算G的梯度
- 最后使用优化器步骤更新G的参数。
使用真实标签作为损失函数的GT标签可能看起来违反直觉【确实难以理解】,但这使我们能够使用BCELoss的\(*log(x)*\)部分(而不是\(*log(1−x)*\)部分),这正是我们想要的。
1 | ############################ |
第3部分 - 统计报告
最后,我们将进行一些统计报告,并在每个时期结束时,我们将通过生成器推动我们的固定噪声批次,以直观地跟踪G的训练进度。
1 | # 输出训练统计 |
- Loss_D - 判别器损失,计算为所有真实批次和所有假批次的损失之和\(*log(D(x))+log(1−D(G(z))))*\)。
- Loss_G - 生成器损失,计算为 \(*log(D(G(z)))*\).
- D(x) - 对所有真实批次的判别器的平均输出。这个数值应该从接近1开始,然后理论上当G变好时收敛到0.5。
- D(G(z)) - 对所有假批次的判别器的平均输出。第一个数字是在更新D之前,第二个数字是在更新D之后。这些数值应该从接近0开始,然后当G变好时收敛到0.5。
- 两者收敛到0.5可能代表着生成器和判别器的性能相近
结果
最后,让我们看看我们的成果。这里,我们将看到三个不同的结果。
在训练过程中D和G的损失是如何变化的
1 | plt.figure(figsize=(10,5)) |
在每个周期上可视化G在固定噪声批次的输出
1 | fig = plt.figure(figsize=(8,8)) |
一批真实数据和G的一批假数据
1 | # 从数据加载器中获取一批真实的图片 |