机器人课程报告
机器人课程报告
背景介绍
在本次报告中可以被介绍一种用于武器的炮塔装置的建模。
机械臂在武器中应用较广,主要用于提高武器的稳定性和精准度。例如,在炮塔装置中,机械臂可以帮助精准地瞄准目标,并保持炮塔在移动过程中的稳定。此外,机械臂还可以用于自动装弹,提高射击效率。
对于用于射击的机械臂,例如教材中提及的有人操作的机械装置,其主要作用是快速辅助瞄准。本报告参考描述了一种基于地面的用于射击的模型。这种模型可以对一个确定的方向提供不错的打击能力。且配合汽车的移动或者类似于雷达车那样的平面转动方法,可以转换打击的方向。另外,这个模型具有不错的扩展性,现在的模型是一个近似串联的模型,而在实际应用时,可以通过增加机械臂数量的方式提供更强力的打击。

在本报告中,会对这种模型应用Denavit-Hartenberg的描述方法进一步简化,并分析其移动性,运动学,反运动学,和动力学。
模型建立
这篇报告中介绍的模型如下图所示,它具有6个自由度。在这6个自由度中,其中的4个自由度有转动副提供。其中,三个转动副的轴在同一平面,y轴(或x轴,在不同的计算中可能会有不同地约定方式)始终穿过这个平面,另一个转动副则以y轴为转轴,来控制这个平面的角度。另外两个自由度有滑动副来提供。
模型的描述
基座是一个树立于xz平面的薄板,其上通过螺丝,连接两个固定的竖杆。竖杆和薄板共同构成真正的基座。为了方便运算,并没有将薄板假设为一个与现实中类似用于的模型相同的大小,而是缩小至1500*1000mm。在后续的计算中,这些尺寸将进一步缩小,以方便计算。
由于竖杆的限制,并非全部的薄板的空间都是可用的。第一个连杆是可以在两个竖杆之间滑动的横杆。横杆可以在竖杆提供的长600mm的凹槽中,沿x轴方向滑动。在建模时,并没有使用滑槽约束,而是通过基础约束:要求两个面的平行以及设定运动范围实现。这提供了第一个自由度。
第二个连杆是套在横杆上,沿z轴方向滑动的底座。这个基座相比于其他的部件非常小,这些构建构成了一个双自由的的直角坐标型操作臂。
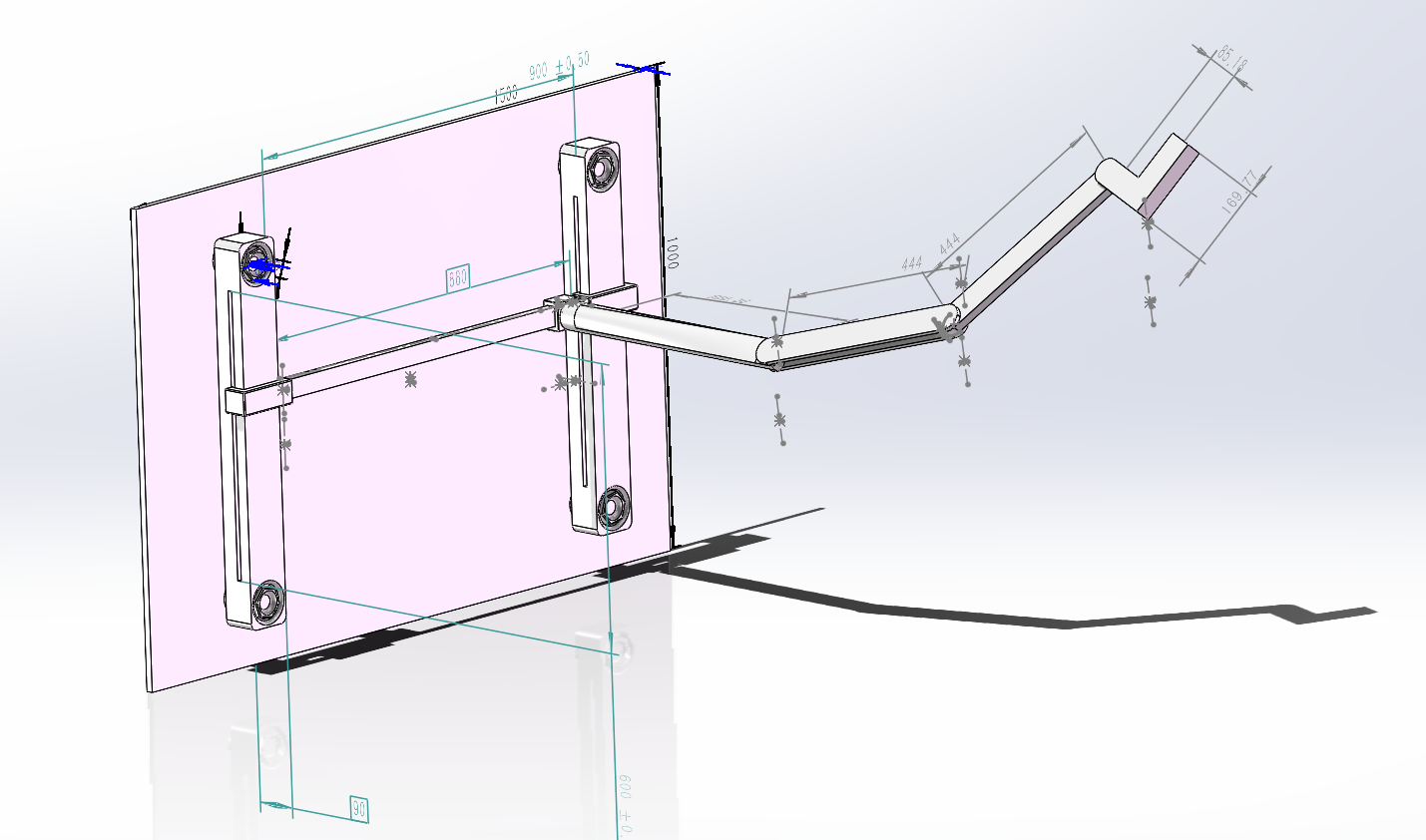
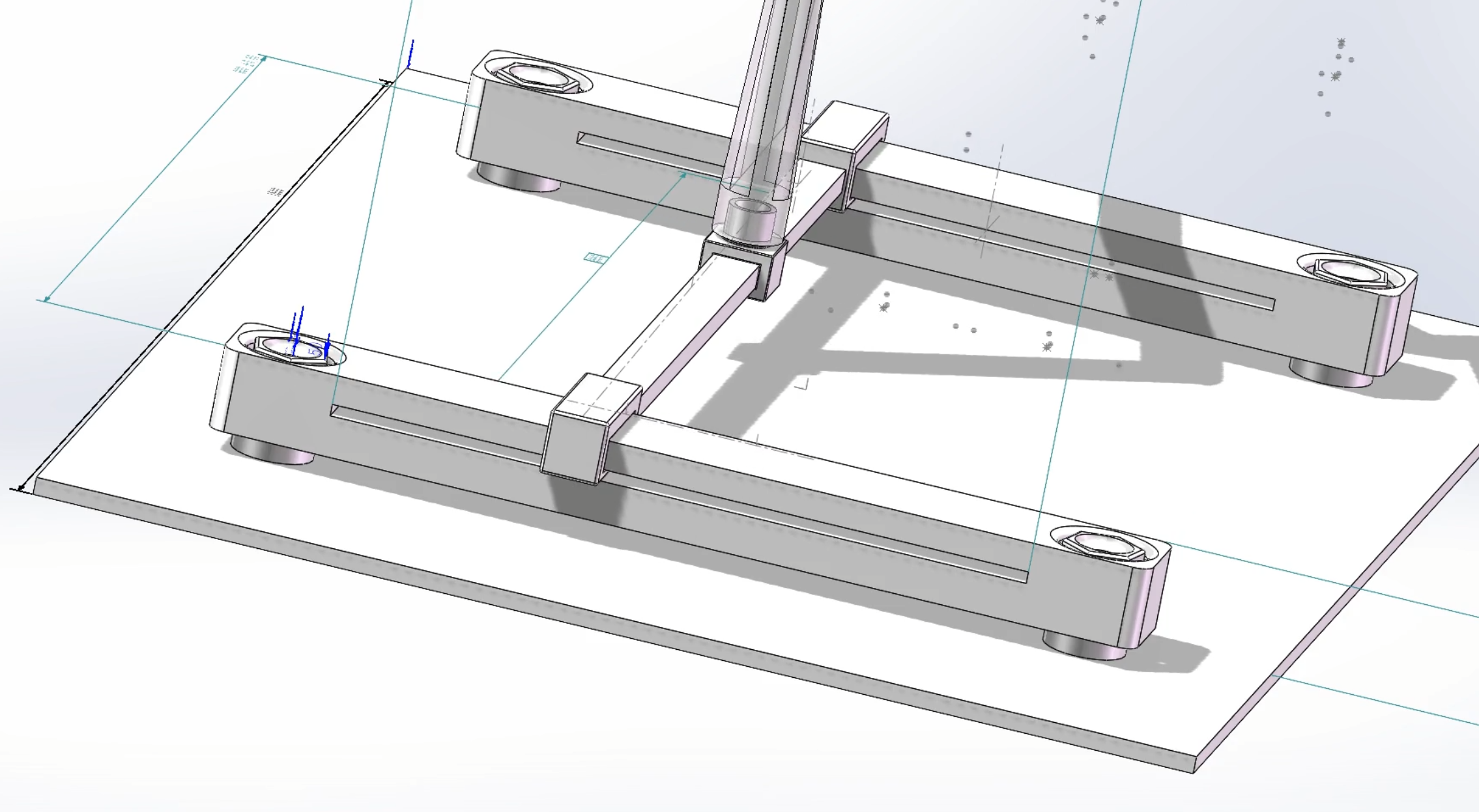
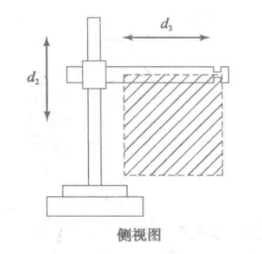
如下图所示,基座的下半部分是一个带空腔的方块,其尺寸与横杆严格匹配,在实际应用过程中,可能需要进一步处理,以满足其滑动的性质。而其上半部分是一个用以满足旋转特性的空心圆柱。这将于第一个连杆结合,构成双自由度基础上的机械臂结构的基座。具体的连接方式可以在上图中透明的连杆中看到。当然,他们并非简单的直接连接,在连杆内部存在一个凸起用来卡住底座。这在现实中似乎是无法生产的,但通过其他方式也可以实现。
经由这种设置,第一个连杆可以在基座上旋转,构成第三个自由度。


一个三个转动副垂直与同一平面的连杆被安装于竖杆上,其中最后一个转动副为腕关节。用于操控模型中建模较为粗糙的执行元件。他们可以在到达他们所在面的几乎所有位置。但是,在这个过程中,连杆的交叉和重叠并没有被很好的考虑。这是这个模型所欠缺的。
这个模型可以在补充材料中找到。
模型简化
一般而言,从solidwork导出为urdf文件已经经过很多尝试。其中,"sw2urdf"和"SolidWorks to URDF Exporter"都是SolidWorks插件,用于将SolidWorks模型导出为URDF文件。根据他们的极少,它们都提供了简化和自动化的工作流程,使用户能够轻松地将SolidWorks设计转换为URDF格式,以便在机器人相关应用程序中使用。其中,"sw2urdf"插件是ROS(Robot Operating System)社区开发的SolidWorks插件。据称,它提供了一个简单的界面,使用户能够直接从SolidWorks中导出URDF文件。并支持SolidWorks中的关节定义、连接关系和惯性属性的导出。它还提供了一些高级功能,如传感器支持和碰撞检测设置。而"SolidWorks to URDF Exporter"插件是由第三方开发的SolidWorks插件。它允许用户将SolidWorks模型导出为URDF文件,并提供了一些自定义选项。插件支持导出关节类型、连接关系、惯性属性和传感器等信息。它还提供了一些额外的功能,如导出模型的CAD几何信息和可视化模型的渲染。
然而,经过我长时间的尝试,一致不能将此模型完全导入python或者matlab的机器人工具箱,再导入过程中,会出现部分约束的失效。同时,这些软件都依赖于坐标系下约束信息的转换,经过大约四个小时的尝试,最终决定在python中重新建模。
Robotics Toolbox for Python (rtb)
Robotics Toolbox for Python,即Python的机器人工具箱,是一款用于研究和教学的开源软件。它与matlab的相应工具箱是同一个作者开发。它包含了一系列用于模拟和分析机器人系统的函数和类。这些工具可以用于机器人的运动学分析、路径规划、视觉处理等多方面。
其中,**DHRobot** 是 Python
机器人工具箱中的一个重要类,用于处理基于
Denavit-Hartenberg(D-H)参数的机器人模型。D-H
参数是一种常用的机器人连杆描述方法,能够通过四个参数来定义连杆之间的几何关系。
dhrobot 类提供了一系列方法来处理基于 D-H
参数的机器人模型,如:
fkine():正向运动学计算。输入为关节参数,输出为末端执行器的位姿。ikine():逆向运动学计算。输入为末端执行器的位姿,输出为关节参数。jacob0()和jacobn():计算机器人的雅可比矩阵,用于描述关节速度与末端执行器线速度和角速度之间的关系。plot():绘制机器人模型。
这些方法使得 **DHr**obot
成为了机器人运动学分析和控制的有力工具。
相比于matlab的相应工具,python的工具箱并不完善。事实上,其文档中存在大量错误,导致很多功能并不能如文档提到的使用方式。尽管如此,相比于Matlab的机器人工具箱,Robotics Toolbox for Python 的优势足以在小规模使用的时候,成为最优解。首先Robotics Toolbox for Python 是完全开源的。这一点对于学习和研究者来说非常有利。事实上,我在实际应用过程中,也对工具箱中的部分实现方法进行了修改。这在matlab中是不能实现的。此外,良好的社区支持使Python拥有庞大的开发者社区,这意味着当遇到问题时,可以很容易地找到解决方案或者获得帮助。而Matlab的社区相对较小。
模型简化
为了方便建模和未来的进一步分析,我撇弃了这个模型中不必要的所有信息,仅保留了建立串联模型的必要数据。在简化后,我基于Denavit-Hartenberg方法,重新建立模型。为了方便之后的计算和分析,将这个模型简化为串联模型。使用两个简单的滑动副来代替,其结构如下:
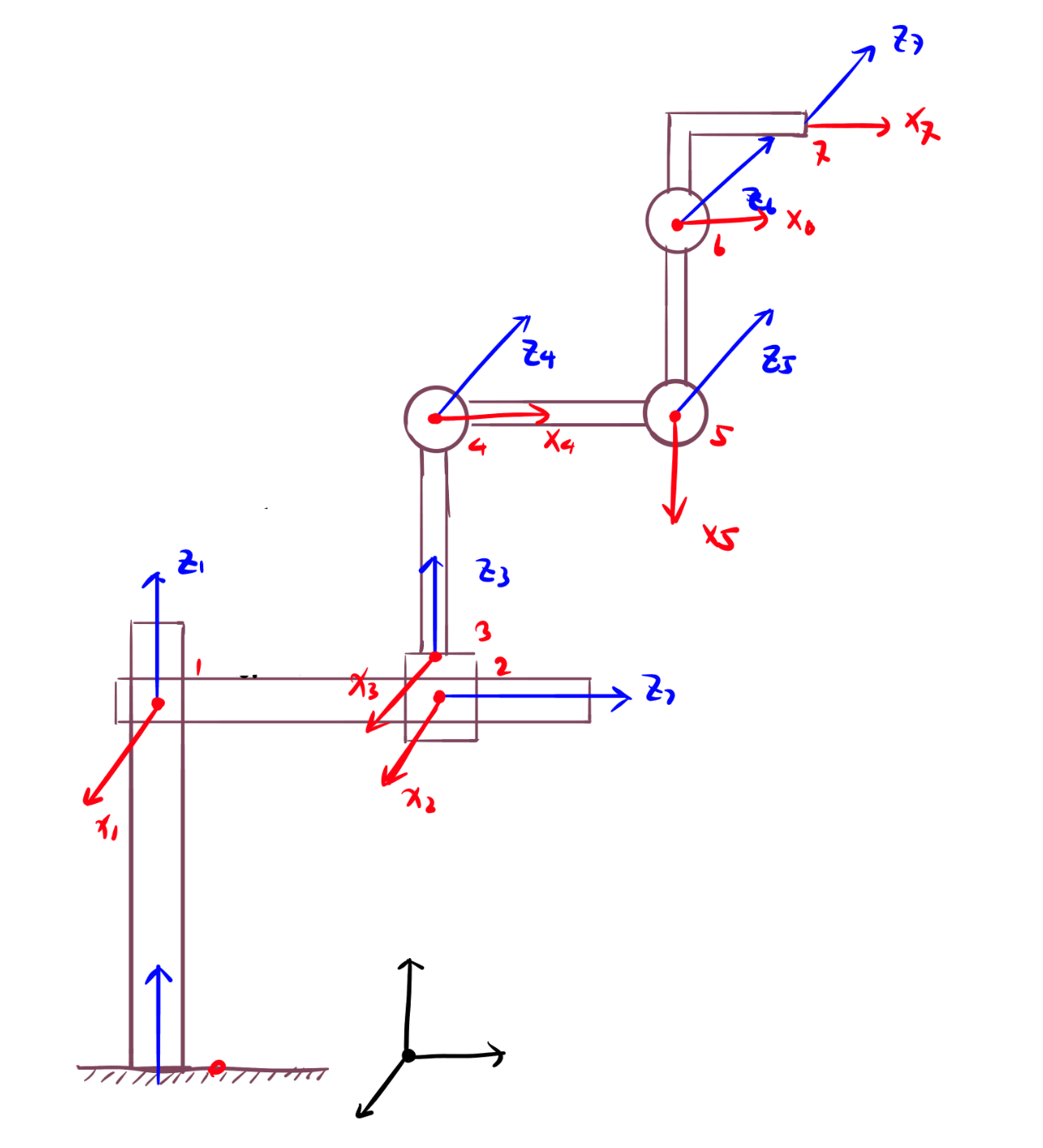
- 必须要注意的是左图中,从第三个关节有一个\(\pi/2\)的扭转,也就是\(x_2 \ x_3\)并非有着相同的方向。
相比于一般的Denavit-Hartenberg方法,我选择了改进的Denavit-Hartenberg方法。事实上,这也是教材所提供和推荐的方法。
改进的Denavit-Hartenberg方法是一种常用于解析机器人运动学的方法。它通过建立每个关节的坐标系和定义四个参数(连接长度、连接偏转、连接角、关节偏转)来描述从一个关节到下一个关节的变换。这四个参数也被称为Denavit-Hartenberg参数。
在改进的Denavit-Hartenberg方法中,坐标系的选择有所不同。在原始的Denavit-Hartenberg方法中,坐标系是沿着关节轴线和连接线选择的。然而,在改进的方法中,坐标系是沿着关节轴线和垂直于两个关节轴线的平面选择的。这种改变使得坐标系的选择更为直观,也使得参数的计算更为简单。
此外,改进的Denavit-Hartenberg方法还引入了一个新的概念——连杆坐标系。这种坐标系定义在连杆的一端,使得描述连杆的运动变得更加简单。这种方法对于分析具有复杂运动的机器人系统非常有用。
在这个模型的基础上基于改进的Denavit-Hartenberg方法分析:
- 首先找出各关节的轴线。由于我们的所有关节都是滑动副或者转动副,其轴线方向非常容易判断。如上图蓝色线条所在直线即为各关节轴线。需要注意的是,从第三个关节开始,使用的基坐标系与前两个并不相同。这导致第三个关节引入了一个额外的扭转。可以对比两幅图片来得到。
- 找到关节轴之间的公垂线或者关节轴之间的交点,用来确认原点位置和确认z轴的指向,这些信息已在上图中标出。
- 使x轴沿公垂线指向,已使用红线在上图中标出。
- 分析其连杆参数:
| \(i\) | \(a_i\) | \(\alpha_i\) | \(d_i\) | \(\theta_i\) |
|---|---|---|---|---|
| 1 | \(0\) | 0 | \(offset\) | \(0\) |
| 2 | \(0\) | \(\pi/2\) | \(offset\) | \(\pi/2\) |
| 3 | \(0\) | \(-\pi/2\) | \(10\) | \(offset\) |
| 4 | \(5\) | \(0\) | \(0\) | \(offset\) |
| 5 | \(5\) | \(0\) | \(0\) | \(offset\) |
| 6 | \(5\) | \(\pi/4\) | \(0\) | \(offset\) |
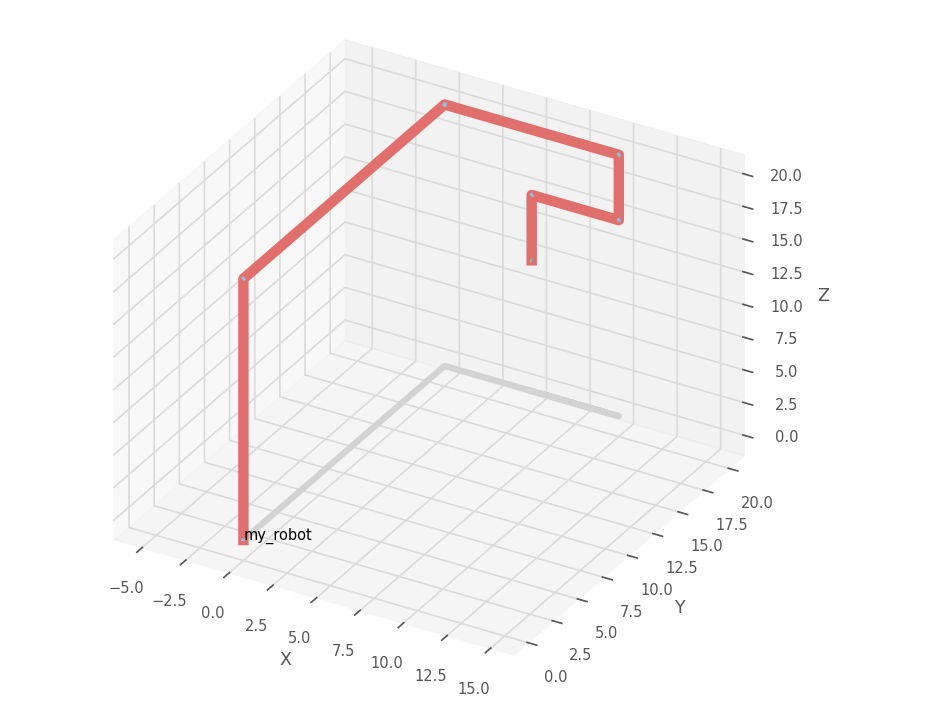
根据分析得到的连杆信息,在python中建模得到上图,这证明了分析的正确性。
运动学分析
运动学分析
运动学分析主要研究的是机器人的运动特性,而不涉及力和力矩等因素。运动学可以分为正向运动学和逆向运动学两部分。这里我们主要介绍正向运动学分析,或者说前向运动学分析。正向运动学分析是根据机器人的关节参数确定其末端执行器位置和姿态的过程。简单来说,就是通过机器人的关节角度来计算机器人手臂的位置和方向。这是机器人导航、路径规划以及进行精确操作所必需的。正向运动学的历史可以追溯到20世纪50年代,当时人们开始研究如何使用计算机来控制机器人的运动。这一研究领域的发展推动了工业机器人的普及以及自动化生产的发展。
基于这些介绍,我们进行运动学分析,首先,我们使用变换矩阵计算一个简单的模型。
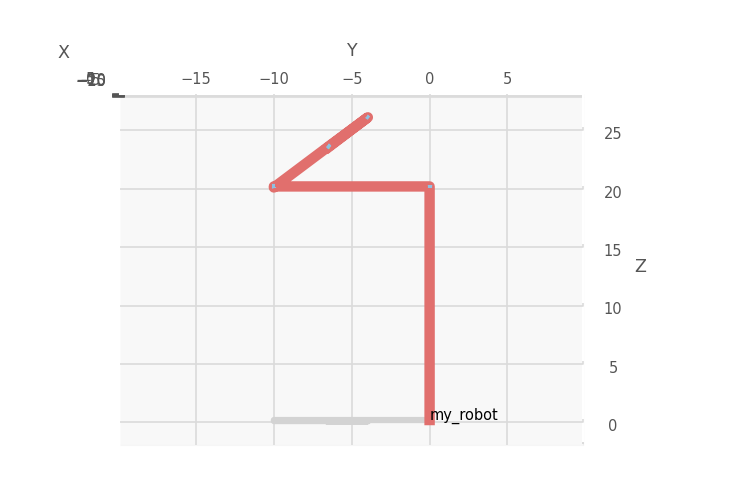
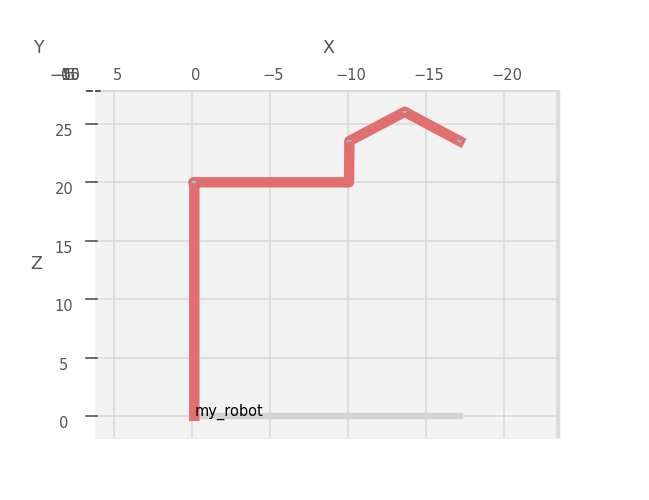
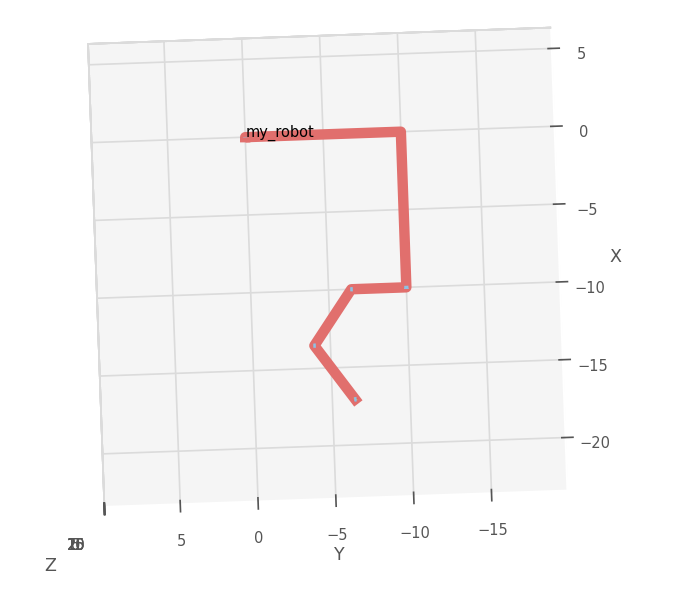
首先从基坐标系到第一个坐标系,第一个关节是一个滑动副,只有沿轴向的平移。在DH方法中,\(z\)轴是轴向方向,因此,易得第一个变换矩阵:
\[ T_0^1 = \left(\begin{array}{cccc}1& 0& 0&0\\0&1&0&0\\0&0&1&20\\0&0&0&1\end{array}\right) \]
第二个关节也是平移,由于两个杆的轴向方向并不相同,因此涉及到坐标系的旋转。新的z轴方向应该指向y轴负方向,因此也是第一个坐标系的y轴负方向。同时,x轴指向原本的z轴方向(注意这里跟之前的DH推到的x轴方向的并不相同),因为基坐标系做了调整。根据预设,应该沿新的z轴方向平移10的距离,得到第二个转换矩阵:
\[ T_1^2 = \left(\begin{array}{cccc}0& -1& 0&0\\0&0&-1&-10\\1&0&0&0\\0&0&0&1\end{array}\right) \]
第三个关节是一个绕原本的y轴旋转的关节。在预设中,设定其旋转\(\pi/4\)。同时,两个坐标系在y轴上相聚10个单位长度。用相同的方法得到新的转换矩阵:
\[ T_2^3 = \left(\begin{array}{cccc} &0.7071 &-0.7071 &0 &0\\ &0 &0 &1 &10\\ &-0.7071 &-0.7071 &0 &0\\ &0 &0 &0 &1\end{array}\right) \]
第四个关节是一个转动副。有\(-\pi/4\)的旋转预设,同时在x轴上有5个单位长度的距离。得到新的矩阵:
\[ T_3^4 = \left(\begin{array}{cccc} &0.7071 &-0.7071 &0 &5\\ &0 &0 &-1 &0\\ &0.7071 &0.7071 &0 &0\\ &0 &0 &0 &1 \end{array}\right) \]
第五个关节和第六个关节都是转动副,其本身与第四个关节相似,因此不设计新的预设增加计算复杂度。在这种情况下,新的两个转换矩阵为:
\[ T_4^5 = \left(\begin{array}{cccc} &0 &-1 &0 &5\\ &1 &0 &0 &0\\ &0 &0 &1 &0\\ &0 &0 &0 &1 \end{array}\right)\ T_5^6 = \left(\begin{array}{cccc} &1 &0 &0 &5\\ &0 &1 &0 &0\\ &0 &0 &1 &0\\ &0 &0 &0 &1 \end{array}\right) \]
最后将这些矩阵相乘,为了加快计算速度,使用numpy这种c语言风格的计算方式,得到:
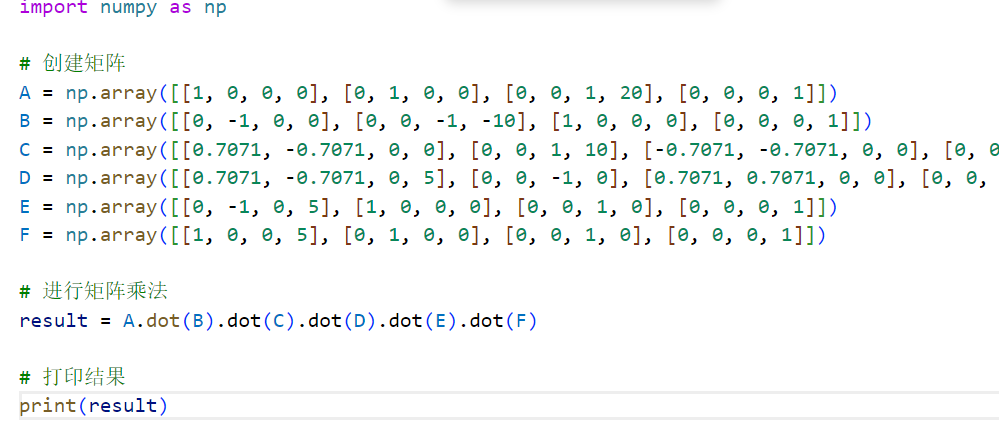

使用python的roboticstoolbox工具箱计算该机械臂的运动学,分别使用A( )方法和fkine( )方法,得到相同的结果:
\[ \begin{pmatrix}-0.7071 & 0.7071 & 0 & -17.07 \\-0.5 & -0.5 & -0.7071 & -6.464 \\-0.5 & -0.5 & 0.7071 & 23.54 \\0 & 0 & 0 & 1\end{pmatrix} \]
操作臂子空间描述
为了我方便计算,我们认为元件3固定,前两个平移关节的关键参数分别设置为[20,10],我们只考虑后四个关节。
操作臂子空间,通常被称为工作空间,指的是机器人操作臂在所有可能的关节配置下能够到达的空间区域。这个空间是由操作臂末端执行器(例如,夹具或工具)在物理空间中的所有可能位置和方向构成的。操作臂子空间的大小和形状取决于机器人的几何结构,包括关节的数量,类型(旋转或平移)以及它们的排列方式。
子空间的符号表示
我们分别使用\(\alpha,\beta,\gamma,\epsilon\)个符号表示后四个关节的角度,并由此计算子空间。为了方便符号计算,我们在列出符号矩阵之后,使用matlab的符号计算而不是python的符号计算。这是因为matlab的符号计算效率远高于python。
\[ \begin{aligned} & T_2^3 = & \left(\begin{array}{cccc} \cos (\alpha) & -\sin (\alpha) & 0 & 0 \\ 0 & 0 & 1 & 10 \\ -\sin (\alpha) & -\cos (\alpha) & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) \end{aligned} \]
\[ \begin{aligned}& T_3^4= & \left(\begin{array}{cccc}-\sin (\beta) & -\cos (\beta) & 0 & 5 \\0 & 0 & -1 & 0 \\\cos (\beta) & -\sin (\beta) & 0 & 0 \\0 & 0 & 0 & 1\end{array}\right)\end{aligned} \]
\[ \begin{aligned}& T_4^5= & \left(\begin{array}{cccc}-\sin (\gamma) & -\cos (\gamma) & 0 & 5 \\\cos (\gamma) & -\sin (\gamma) & 0 & 0 \\0 & 0 & 1 & 0 \\0 & 0 & 0 & 1\end{array}\right)\end{aligned} \]
\[ \begin{aligned}& T_5^6 =& \left(\begin{array}{cccc}\cos (\varepsilon) & -\sin (\varepsilon) & 0 & 5 \\\sin (\varepsilon) & \cos (\varepsilon) & 0 & 0 \\0 & 0 & 1 & 0 \\0 & 0 & 0 & 1\end{array}\right)\end{aligned} \]
求死者的乘积得到子空间矩阵:
\[ \begin{aligned} & T_2^6 =\text { ( } \\ & \left(\begin{array}{cccc} \sin (\varepsilon) \sigma_4-\cos (\varepsilon) \sigma_3 & \cos (\varepsilon) \sigma_4+\sin (\varepsilon) \sigma_3 & \sin (\alpha) & 5 \cos (\alpha)-5 \cos (\alpha) \sin (\beta)-5 \cos (\alpha) \cos (\beta) \cos (\gamma)+5 \cos (\alpha) \sin (\beta) \sin (\gamma) \\ \sin (\varepsilon) \sigma_5-\cos (\varepsilon) \sigma_6 & \cos (\varepsilon) \sigma_5+\sin (\varepsilon) \sigma_6 & 0 & 5 \cos (\beta)-5 \cos (\beta) \sin (\gamma)-5 \cos (\gamma) \sin (\beta)+10 \\ \cos (\varepsilon) \sigma_1-\sin (\varepsilon) \sigma_2 & -\cos (\varepsilon) \sigma_2-\sin (\varepsilon) \sigma_1 & \cos (\alpha) & 5 \sin (\alpha) \sin (\beta)-5 \sin (\alpha)+5 \cos (\beta) \cos (\gamma) \sin (\alpha)-5 \sin (\alpha) \sin (\beta) \sin (\gamma) \\ 0 & 0 & 0 & 1 \end{array}\right) \end{aligned} \]
\[ avec\quad\begin{aligned}& \sigma_1=\cos (\beta) \cos (\gamma) \sin (\alpha)-\sin (\alpha) \sin (\beta) \sin (\gamma) \\& \sigma_2=\cos (\beta) \sin (\alpha) \sin (\gamma)+\cos (\gamma) \sin (\alpha) \sin (\beta) \\& \sigma_3=\cos (\alpha) \cos (\beta) \cos (\gamma)-\cos (\alpha) \sin (\beta) \sin (\gamma) \\& \sigma_4=\cos (\alpha) \cos (\beta) \sin (\gamma)+\cos (\alpha) \cos (\gamma) \sin (\beta) \\& \sigma_5=\sin (\beta) \sin (\gamma)-\cos (\beta) \cos (\gamma) \\& \sigma_6=\cos (\beta) \sin (\gamma)+\cos (\gamma) \sin (\beta)\end{aligned} \]
代入\(\alpha = \beta = \gamma = \epsilon = \pi/6\)验证得:
\[ \left(\begin{array}{cccc}0 & \frac{\sqrt{3}}{2} & \frac{1}{2} & 0 \\-1 & 0 & 0 & 10 \\0 & -\frac{1}{2} & \frac{\sqrt{3}}{2} & 0 \\0 & 0 & 0 & 1\end{array}\right) \]
子空间矩阵的代数运算
然而在绘图过程中,基于einsum的绘图方式不能计算如此复杂的矩阵乘法,因此将计算结果转会python进一步处理。首先为了方便计算,在对于四个关节,均在其qlim中取出10个满足约束条件的取值,代入计算相应矩阵,得到:
\[ T_2^3(4,4,10),\ T_3^4(4,4,10),\ T_4^5(4,4,10), \ T_5^6(4,4,10) \]
进行如下规则的矩阵乘法:\(a_{ija}\cdot b_{jlb} = c_{il(a*b)}\)。然而这种计算方式不能使用爱因斯坦求和约定简单求和,因此牺牲部分性能,设计以下函数用于计算这种特殊的乘法:
1 | def foi(A,B): |
这种计算方式会导致计算结果出现微小的偏差,这跟python的计算方式有关。比如上述\(\pi/6\)的例子在这种计算模式下得到的结果:
\[ \begin{pmatrix}-1.94289029e-16 & 8.66025404e-01 & 5.00000000e-01 & -8.88178420e-16 \\-1.00000000e+00 & -2.14607521e-16 & 0.00000000e+00 & 1.00000000e+01 \\1.03585218e-16 & -5.00000000e-01 & 8.66025404e-01 & 4.44089210e-16 \\0.00000000e+00 & 0.00000000e+00 & 0.00000000e+00 & 1.00000000e+00\end{pmatrix} \]
可以看到出现了\(10^{-16}\)的误差,但这种误差是可以忽略的。
在这种计算模式下,将四个矩阵相乘,得到:\(T_2^6 (4,4,10000)\)
计算子空间分布
按照计算规则:\(T_2^6 (4,4,10000)\cdot \left(0,10,20,1\right) = Op(4,10000)\),并使用第一维的前三个数字作为坐标绘制散点图,得到计算结果:
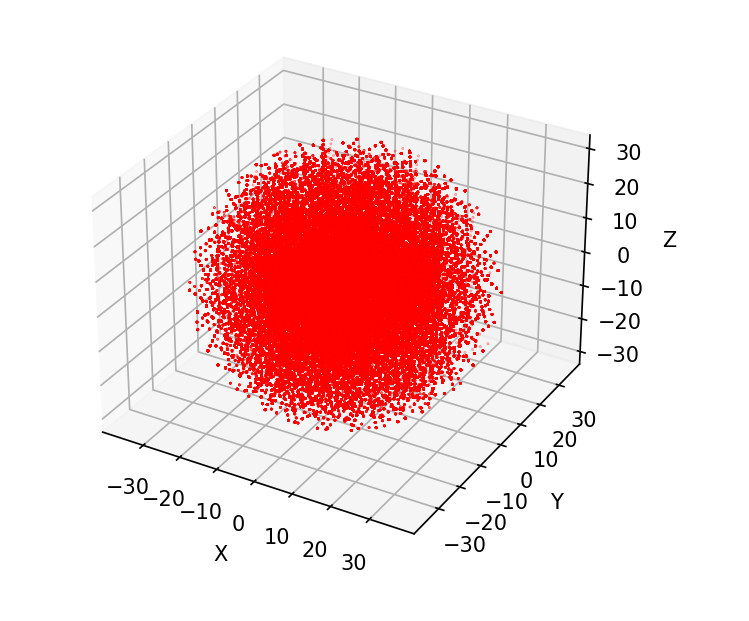
可以看到计算的最终结果类似于球,这可能与机械臂足够多的自由度有关。事实上,我们可以很简答的抽象出当前的结果。因为后三个关节是在同一平面内的三个转动副,我们可以认为它可以确定一个圆形的平面,圆形的半径取决于其机械臂能达到的范围。而第3个关节或者倒数第四个关节是一个过圆心的(事实上,如果不考虑杆之间的碰撞,第三个和第四个杆的连接处就是圆心)的转动副。自然而然就会形成球状的子空间分布。
具体的计算代码可以在补充文件中找到,相应的代码已经全部转化为python代码(包括原本使用matlab的部分),文件被命名为transformation_calculation.py,依赖于数学运算库numpy和绘图库matplotlab。
逆运动学分析
逆运动学分析是机器人学中的一个重要方向,它的目标是通过给定机器人末端执行器的位置和姿态,来求解机器人的关节参数。简单来说,就是根据机器人手臂的位置和方向来计算机器人的关节角度。
逆运动学的解决方案并不总是存在,也并不总是唯一的。例如,对于某些机器人,可能没有一组关节角度能够使末端执行器达到指定的位置和姿态。另一方面,对于具有冗余自由度的机器人,可能存在多个关节角度组合,都可以使末端执行器达到相同的位置和姿态。
逆运动学的计算通常比较复杂,可能需要使用数值方法,如迭代或优化技术。在某些特定情况下,也可能存在解析解。逆运动学在机器人路径规划、操作控制等方面具有重要应用。
解的存在性
我们知道,对于所有只包含转动关节和移动关节的串联型6自由度机构来说,一定是可解的,这也是我们再简化机构的过程中,以串联型为目标的简化原理。
逆运动学分析
代数解法
假设底座固定,考虑四自由度的解法。必须要注意的是,第4、5个关节本身具备\(\pi/2\)的offset,在后续的计算和绘图中,并没有考虑这些offset,但在绘图中这些是必须要注意的。
我们先前已经计算了通用的\(T_2^6(\alpha,\beta,\gamma,\epsilon)\),而假定我们已经得到执行坐标系的转换矩阵\(T_{2,object}^6\)。基于代数解法,存在以下方程:
\[ T_2^6(\alpha,\beta,\gamma,\epsilon) = T_{2,object}^6 \]
在前面的过程中,我们已经看到了这种计算的复杂性,对此我们不进行手动的计算。我们假设:
\[ T_{2,object}^6 = \left(\begin{array}{cccc}0 & \frac{\sqrt{3}}{2} & \frac{1}{2} & 0 \\-1 & 0 & 0 & 10 \\0 & -\frac{1}{2} & \frac{\sqrt{3}}{2} & 0 \\0 & 0 & 0 & 1\end{array}\right) \]
即我们之前使用的假设,来尝试使用matlab求解,得到:
\[ \begin{aligned} & \alpha = \left(\begin{array}{c} \frac{\pi}{6} \\ \frac{\pi}{6} \end{array}\right) \ \beta = \left(\begin{array}{c} \frac{\pi}{6} \\ \frac{5 \pi}{6} \end{array}\right) \ \gamma = \left(\begin{array}{c} \frac{\pi}{6} \\ \frac{5 \pi}{6} \end{array}\right) \ \varepsilon = \left(\begin{array}{c} \frac{\pi}{6} \\ \frac{5 \pi}{6} \end{array}\right) \end{aligned} \]
有两组解,解得数量符合预期,两组解中,\(\alpha\)取值相同,是因为\(\alpha\)决定了所在平面。
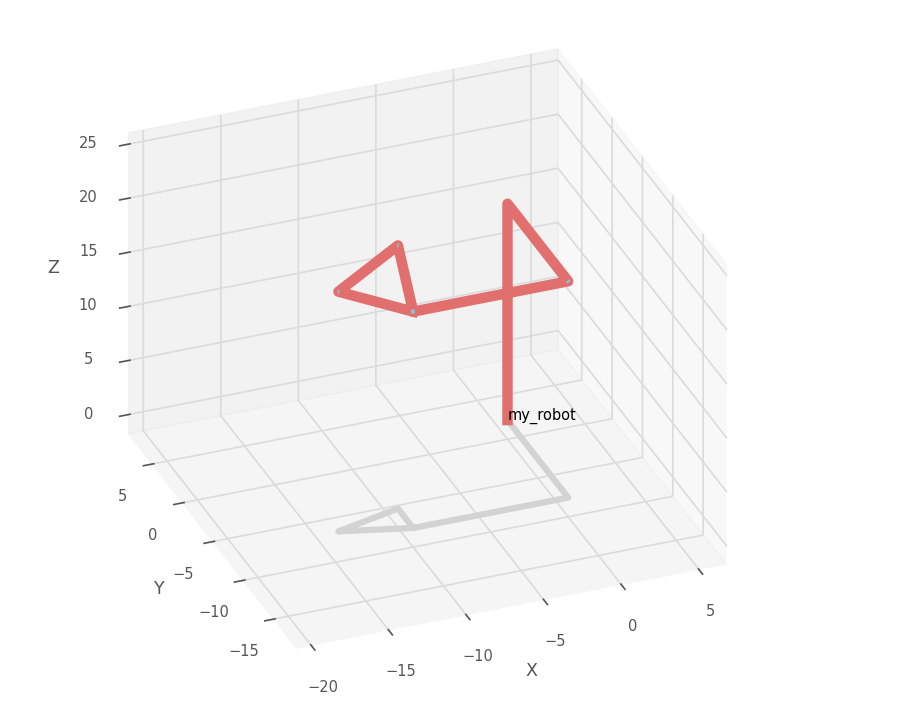
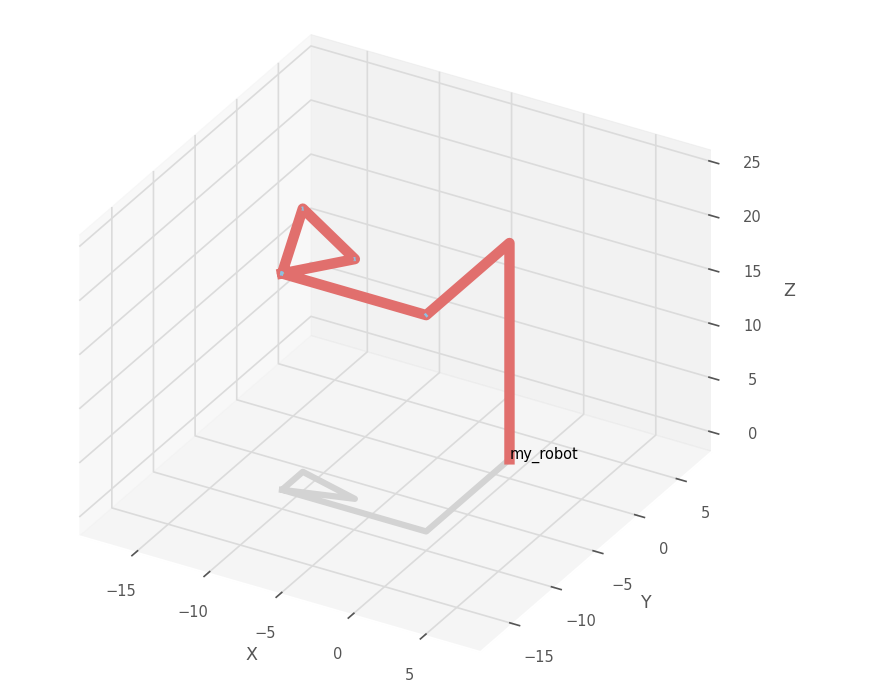
两组解得到了完全相同的结果。但请注意,这两幅图片的杆的顺序并不相同\(\pi/6\)的环是从当前角度看逆时针形成的,而\(5\pi/6\)的版本则是顺时针形成的。为了使这一点更加明显,我用相同的方式计算了这一组结果:
\[ \begin{aligned} & \alpha = \left(\begin{array}{c} \frac{\pi}{6} \\ \frac{\pi}{6} \end{array}\right) \ \beta = \left(\begin{array}{c} \frac{\pi}{6} \\ \frac{2 \pi}{3} \end{array}\right) \ \gamma = \left(\begin{array}{c} 0 \\ \pi \end{array}\right) \ \varepsilon = \left(\begin{array}{c} \frac{\pi}{6} \\ \frac{2 \pi}{3} \end{array}\right) \end{aligned} \]
其图像如下,在这种假设下,可以很清晰的看到两者的不同。同时第一附图出现了交叉,这是不被允许的,所以这种情况可以认为有实际上的唯一解。
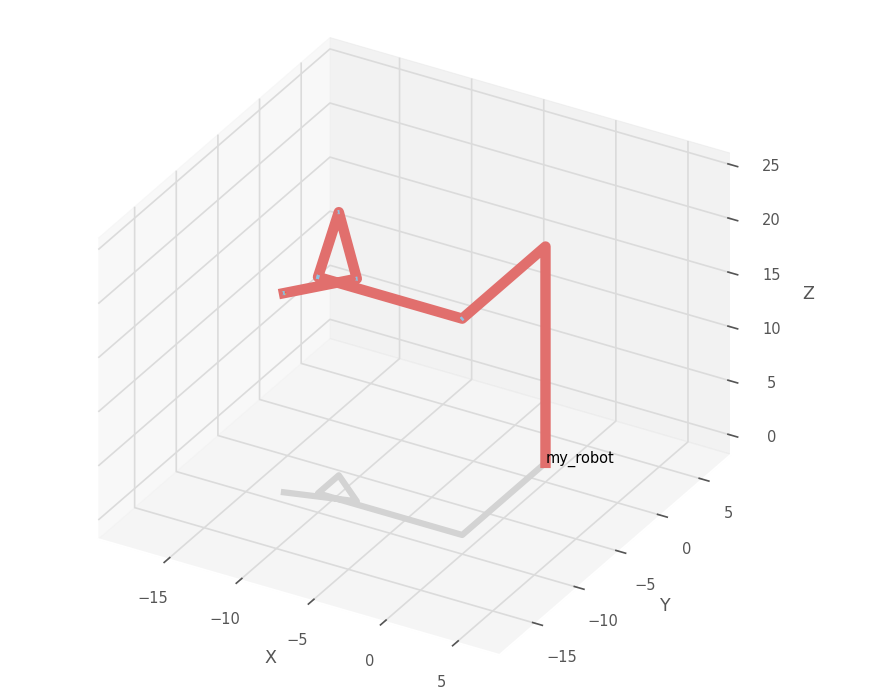
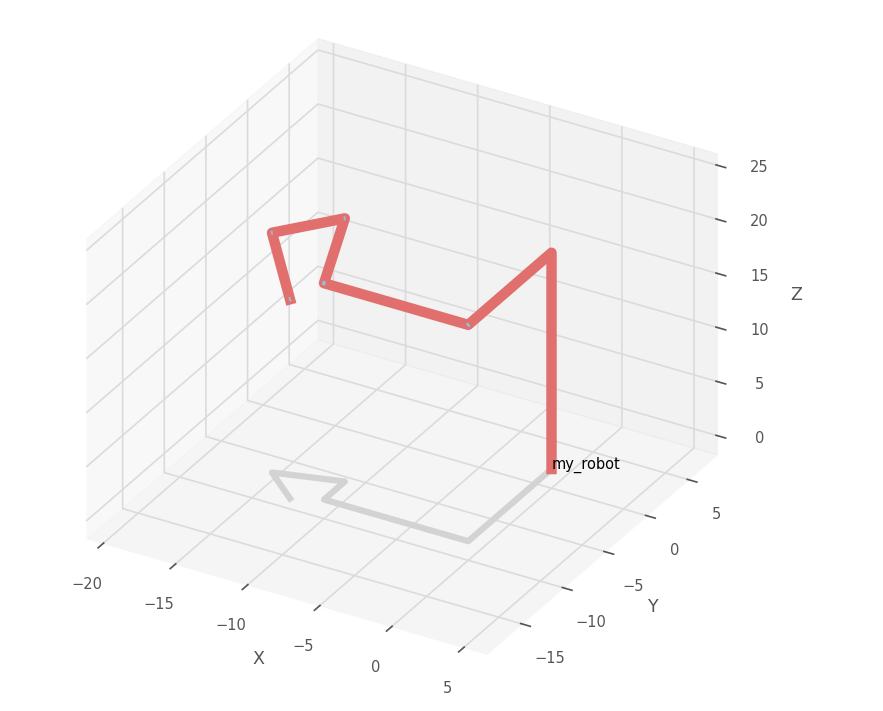
几何解法
在几何解法中,我们假设我们已知腕坐标系的原点坐标和工作端坐标系z轴方向,并以此进行逆动力学分析。我们依然假设底座固定,考虑四自由度的解法。
为了方便计算,我们假设在基坐标系中,工作端坐标系的原点为:\(\left(\begin{array}{c} \frac{5 \sqrt{3}}{4}-\frac{15}{4} , \frac{5 \sqrt{3}}{2}+\frac{15}{2} , \frac{5 \sqrt{3}}{4}-\frac{5}{4} \end{array}\right)\),其z轴指向\(\left(\begin{array}{c} \frac{1}{4} , -\frac{\sqrt{3}}{4} , \frac{\sqrt{3}}{2} \end{array}\right)\),基座原点坐标:\((-10,20,20)\),
首先正如前文所提及,能够影响后三个杆所在平面,或者说后三个转轴的垂直平面,只由第三个关键的角度\(\alpha\)影响。因此,我们一旦知道了腕z轴指向与基坐标系或者底座坐标系的z轴(事实上他们z轴重合),我们就可以很简单的求出\(\alpha\)角。
考虑在约定上,\(\alpha\in[-\pi,\pi]\),得到\(\alpha\):
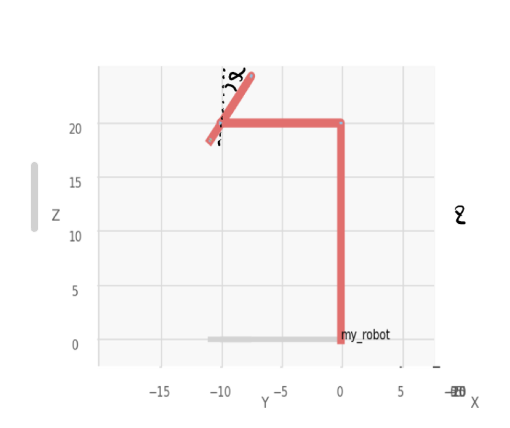
\[ \alpha = \cos^{-1}\left(\frac{z_6\cdot z_1}{||z_6||\times||z_1||}\right) = \pi/6 \]
然后我们就可以在三个轴所在的平面上解决这个三自由度的逆运动学问题。首相将所有的坐标转化为平面内的坐标,取关节4为坐标原点,原本的x方向的负方向为新的平面坐标的x方向。得到目标点在该平面内的新坐标:\((5/2(\sqrt3-1),5/2(-\sqrt3+1))\)直接应用余弦定理得到:\(\gamma = 0,\pi\),而\(\varepsilon\)取决于工作端坐标系z轴方向。\(\left(\begin{array}{c} \frac{1}{4} , -\frac{\sqrt{3}}{4} , \frac{\sqrt{3}}{2} \end{array}\right)\)向该平面投影,计算角度得到\(\varepsilon= \pi/6,5\pi/6\)这与之前给出的结果相同。
\[ cos(\gamma) = \frac{l_1^2+l_2^2-(x^2+(y+5)^2)}{2l_1l_2} = 0 \]
\[ \beta = \frac{\pi-\gamma}{2}+\arctan(\frac{x}{y+5}) = \pi/6,5\pi/6 \]
机器人工具箱给出的逆动力学方法
python的机器人工具箱极其——极其到从来没有见过般极其混乱,文档中所有的说明基本全部错误,我只能翻阅源代码以及查找github上与我类似的受害者和为这些受害者提供帮助的好心人的报告。
我为程序提供的逆运动学分析原型如图右,其具体参数:q = [0, 0, pi/6, pi/6, 0, pi/6],而初始姿态如图左,我会使用不同的方式进行逆运动学分析。
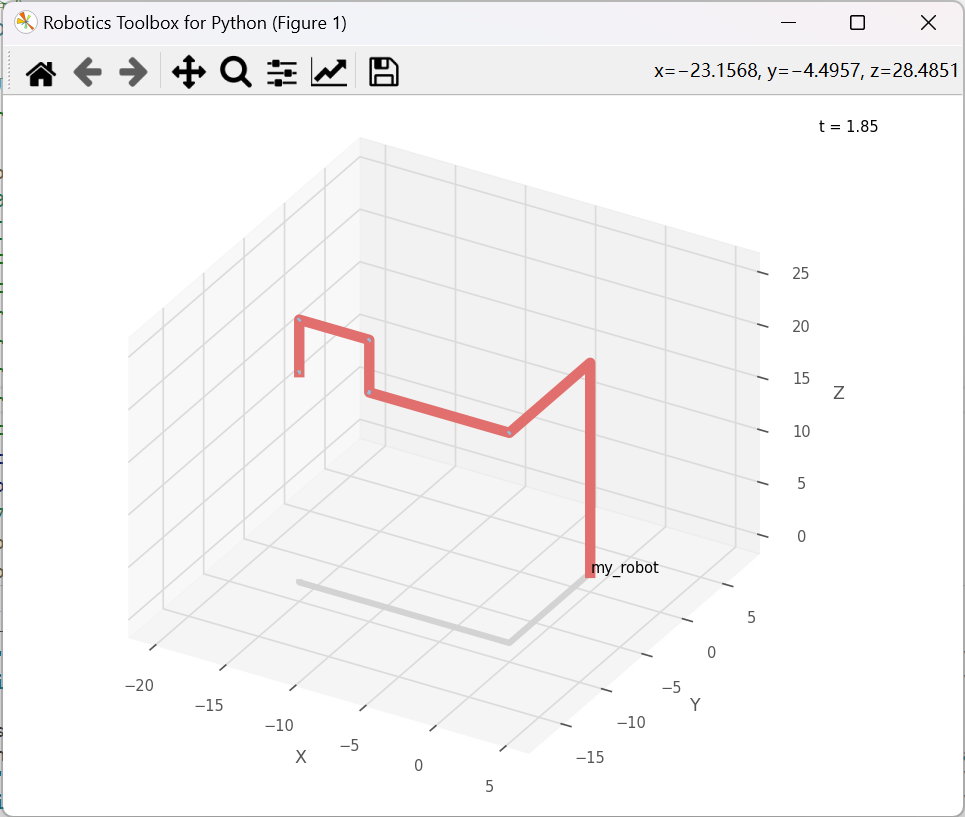
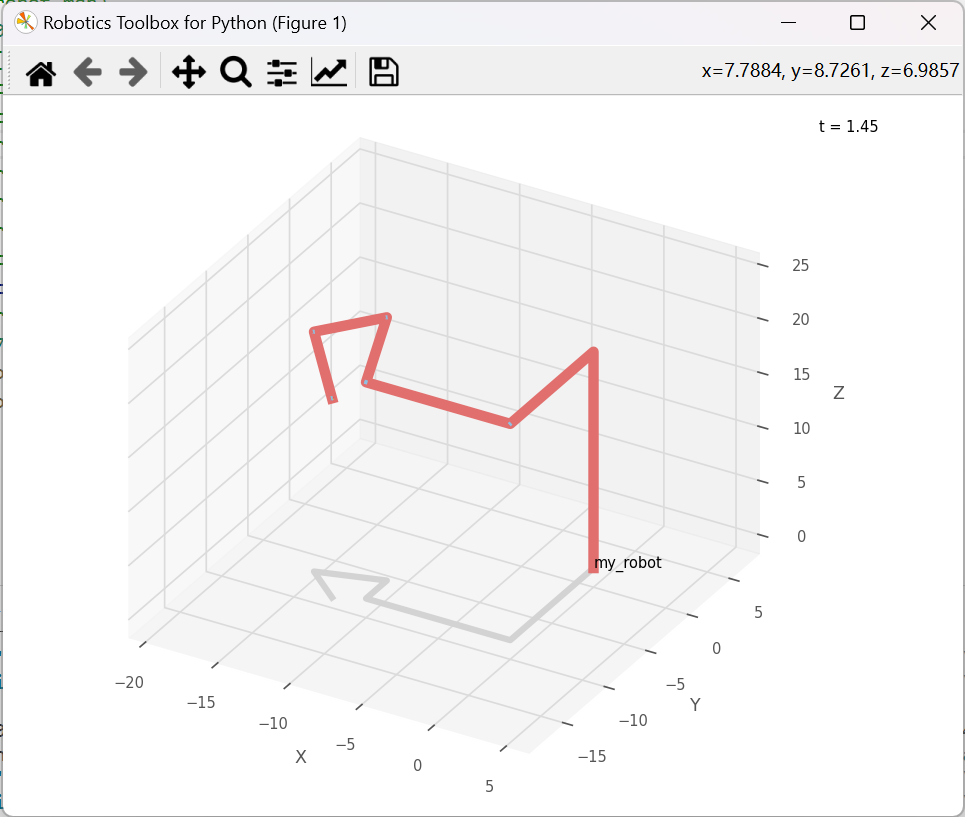
Levenberg-Marquardt方法
Levenberg-Marquardt方法是一种用于求解非线性最小二乘问题的优化算法,也被广泛应用于逆运动学分析。在求解逆运动学问题时,我们往往需要最小化某种误差函数,例如目标位置和机器人末端执行器实际位置之间的差距。Levenberg-Marquardt方法就是为了找到最小化这种误差的关节角度配置。
Levenberg-Marquardt方法结合了梯度下降法和牛顿法的思想,通过引入一个调整因子来平衡两者。当调整因子较大时,算法更接近于梯度下降法,这在误差函数的值较大时有利于快速收敛;当调整因子较小,算法更接近于牛顿法,这在误差函数的值较小时有利于精确求解。
在python工具箱中,通过函数以下函数可以实现计算,但必须要注意的是这个程序定义在ETS.py中,而不是DHRobot中。所以在调用时必须使用robot.ets().ikine_LM
1 | def ikine_LM( |
经过iterations=6930代迭代,历时8.74s,程序找到了235个可行解,并在其中选择了最小值,这个值的残差只有:4.55e-07
q=[2.537, 2.163, 0.5236, -0.3155, 0.9399, 0.4228]
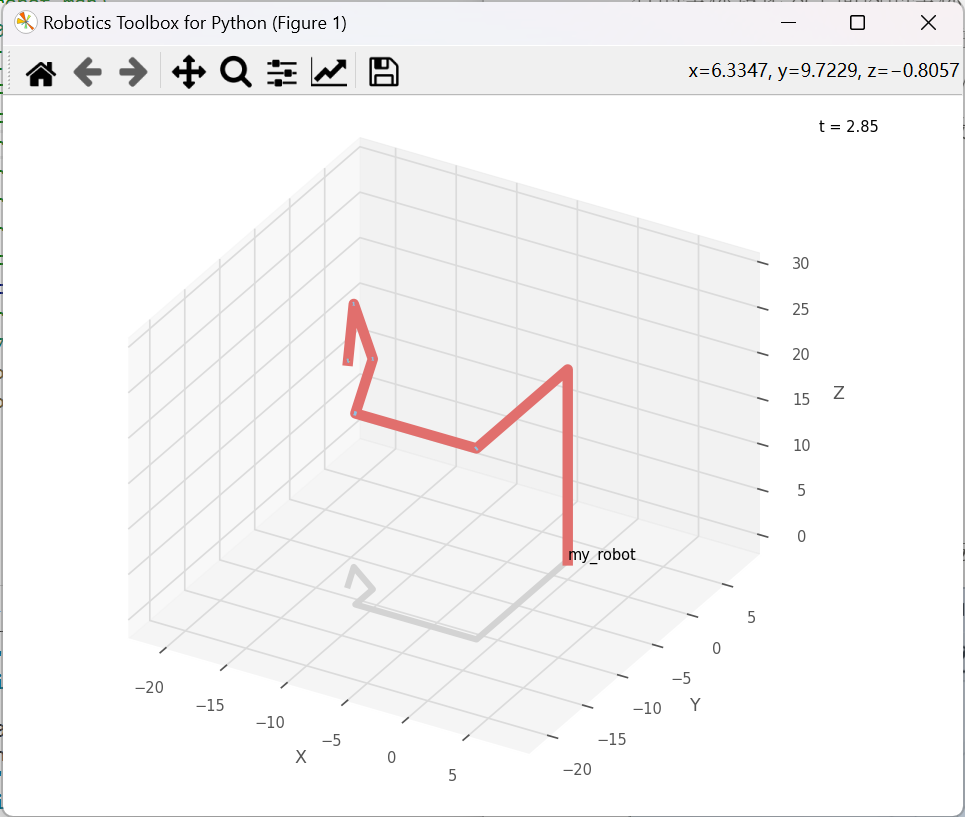
Newton-Raphson 方法
牛顿-拉弗森(Newton-Raphson)方法是一种迭代法,主要用于求解非线性方程或者系统的数值解,也被广泛应用于逆运动学分析。
牛顿-拉弗森方法的基本思想是,对于一个非线性方程f(x)=0,我们可以在一个初始解x0附近将f(x)用泰勒级数进行展开。如果只保留到一阶项,就得到了f(x)在x0处的线性近似,解这个线性方程就可以得到一个新的解x1。然后在x1处再做一次线性近似,以此类推,通过反复迭代,可以使得解逐渐接近真实解。
值得注意的是,牛顿-拉弗森方法需要选择一个合适的初始解,如果初始解离真实解太远,可能会导致迭代过程难以收敛。这可能与实际应用中给出的解的质量不尽人意有关。
其函数本身定义与上一个方法类似,在这里不再赘述,最终计算结果,历时20.11s,进行了99979次迭代,仅给出了118的残差,并不尽人意。
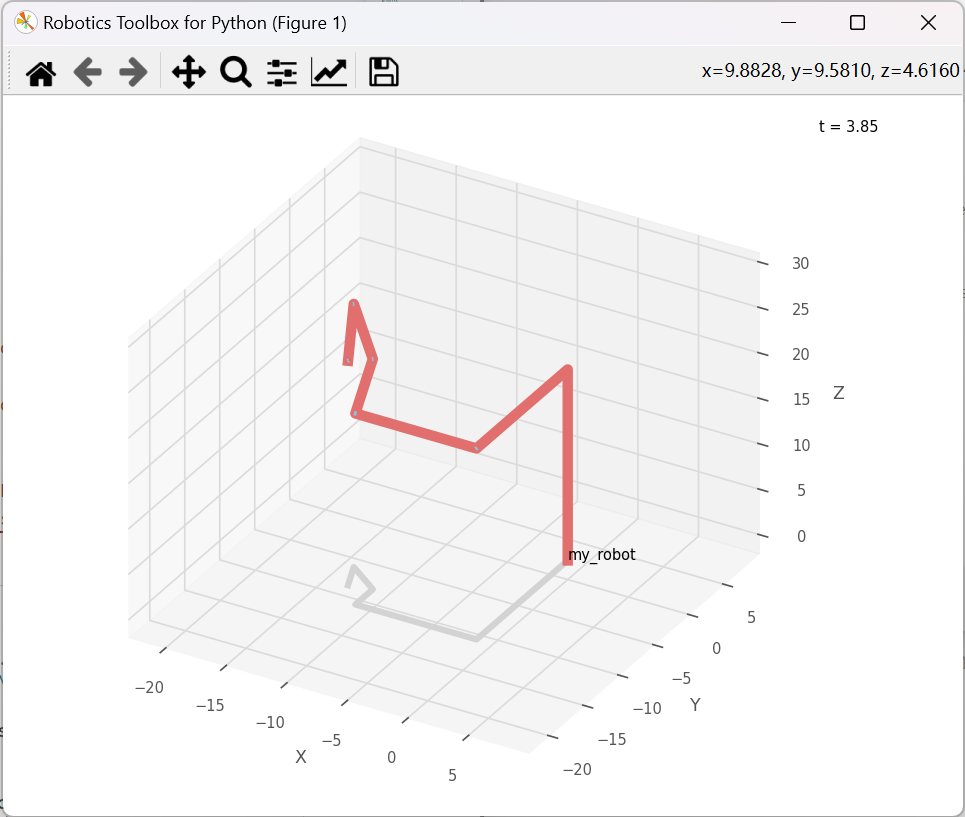
速度和静力
机器人速度和静力的研究涵盖了机器人运动学和动力学的重要部分。速度是机器人学的一个关键分支,主要研究机器人的速度、加速度以及它们与关节速度和关节加速度之间的关系。这是控制机器人精确运动的基础。静力研究,它主要涉及机器人在静止或缓慢移动时受到的力和力矩。这些力和力矩决定了机器人的稳定性和抓取能力,对于设计实现复杂操作(如搬运、装配等)的机器人来说至关重要。
速度和角速度的传递
为了描述关节之间的速度和角速度的传递,我们引入公式:
\[ { }^{i+1} \omega_{i+1}={ }^{i+1} R^i \omega_i+\dot{\theta}{i+1} \]
\[ { }^i v_{i+1}={ }^i v_i+{ }^i \omega_i \times{ }^i P_{i+1} \]
角速度
第一个公式描述了刚体在从坐标系 \(i\) 到坐标系 \(i+1\) 的变换中的角速度关系。其中, \({ }^{i+1} \omega_{i+1}\) 表示坐标系 \(i+1\) 中的角速度, \({ }^{i+1} R^i\) 表示从坐标系 \(i\) 到坐标系 \(i+1\) 的旋转矩阵, \(\omega_i\) 表示坐标系 \(i\) 中的角速度, \(\dot{\theta}_{i+1}\) 表示坐标系 \(i+1\) 相对于坐标系 \(i\) 的角速度变化率, \({ }^{i+1} \hat{Z}_{i+1}^i\) 表示从坐标系 \(i\) 到坐标系 \(i+1\) 的旋转轴的单位向量。
以我们之前计算的从第二个关节到第三个关机的传递矩阵为例:
\[ \begin{aligned} & T_2^3 = & \left(\begin{array}{cccc} \cos (\alpha) & -\sin (\alpha) & 0 & 0 \\ 0 & 0 & 1 & 10 \\ -\sin (\alpha) & -\cos (\alpha) & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) \end{aligned} \]
易得,其旋转矩阵为:
\[ \begin{aligned} & R_2^3 = & \left(\begin{array}{cccc} \cos (\alpha) & -\sin (\alpha) & 0 \\ 0 & 0 & 1 \\ -\sin (\alpha) & -\cos (\alpha) & 0 & \end{array}\right) \end{aligned} \]
同时观察旋转矩阵,发现其旋转轴为原本的y轴方向,即:
\[ \hat Z_{i+1}^i = \left(\begin{array}{c} 0 \\ 1 \\ 0 \end{array}\right) \]
使用python的符号计算功能,可以得到:
\[ \omega_{i+1}^i = \begin{bmatrix} \omega_{i_1}\cos(\alpha) - \omega_{i_2}\sin(\alpha) \\ \omega_{i_3} + \dot\theta \\ -\omega_{i_1}\sin(\alpha) - \omega_{i_2}\cos(\alpha) \end{bmatrix} \]
计算可以在rotation_calculation.py中找到
速度
对于第二个公式,这个公式描述了刚体在坐标系 \(i\) 中的线速度与角速度之间的关系。其中, \({ }^i v_{i+1}\) 表示坐标系 \(i\) 中点 \(i+1\) 的线速度, \({ }^i v_i\) 表示坐标系 \(i\) 中的线速度, \({ }^i \omega_i\) 表示坐标系 \(i\)中的角速度, \({ }^i P_{i+1}\) 表示从坐标系 \(i\) 到坐标系 \(i+1\) 的位移向量。
根据旋转矩阵:
\[ { }^2 P_3=\left(\begin{array}{c}0 \\10 \\0\end{array}\right) \]
使用python的符号计算得到:
\[ v_3 = \begin{bmatrix} -10\omega_{2z} + v_{2x} \\ v_{2y} \\ 10\omega_{2x} + v_{2z} \end{bmatrix} \]
计算过程可以在calculate_linear_velocity.py文件中找到。
雅可比
在机器人运动学中,速度雅可比矩阵将关节速度的变化与末端执行器的线速度之间的关系进行了描述。它是一个 \(m \times n\) 的矩阵,其中 \(m\) 是末端执行器自由度的数量 (通常是 6 ,表示平移和旋转自由度), \(n\) 是机器人关节的数量。
速度雅可比矩阵的元素表示了末端执行器的每个自由度对于每个关节速度的影响。具体而言,速度雅可比矩阵的第 \(i\) 列表示第 \(i\) 个关节速度对于末端执行器的线速度和角速度的影响。
一般来说,雅可比矩阵可以被表示为:
\[ \begin{bmatrix}\frac{\partial f_1}{\partial q_1} & \frac{\partial f_1}{\partial q_2} & \cdots & \frac{\partial f_1}{\partial q_n} \\ \frac{\partial f_2}{\partial q_1} & \frac{\partial f_2}{\partial q_2} & \cdots & \frac{\partial f_2}{\partial q_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial q_1} & \frac{\partial f_m}{\partial q_2} & \cdots & \frac{\partial f_m}{\partial q_n} \end{bmatrix} \]
其中,\(f_i\) 表示末端执行器的第 \(i\) 个自由度(例如,位置分量或旋转分量),\(q_j\) 表示第 \(j\) 个关节变量。
我们使用python的机器人库来计算速度雅可比。
根据文档,机器人库提供了两种计算雅可比矩阵的方法,分别计算Manipulator Jacobian in end-effector frame和Manipulator Jacobian in world frame。
第一种表示方法将雅可比矩阵的计算基于末端执行器的坐标系。它描述了末端执行器在自身坐标系中的速度和姿态与关节速度之间的关系。它可以用于控制末端执行器的线速度和角速度。第二种表示方法将雅可比矩阵的计算基于世界坐标系。它描述了末端执行器在世界坐标系中的速度和姿态与关节速度之间的关系。它可以用于控制末端执行器在世界坐标系中的线速度和角速度。
符号计算的结果过于庞大,不能再报告中展示,可以在jv_equation_0.txt和jv_equation_e.txt中分别找到。具体的计算过程可以在robot_velocity_jacobian.py中找到。
而数值计算的结果,在所有的关节均为初始状态时,分别为
\[ Jacob_e = \left[\begin{matrix}-1.0 & 3.0 \cdot 10^{-49} & 3.1 \cdot 10^{-16} & 5.0 & 0 & 0\\\\-1.8 \cdot 10^{-16} & 0 & 3.8 \cdot 10^{-32} & 5.0 & 5.0 & 0\\\\6.1 \cdot 10^{-17} & 1.0 & 0 & 0 & 0 & 0\\\\0 & 0 & 1.2 \cdot 10^{-16} & 0 & 0 & 0\\\\0 & 0 & -1.0 & 0 & 0 & 0\\\\0 & 0 & 6.1 \cdot 10^{-17} & 1.0 & 1.0 & 1.0\end{matrix}\right] \]
\[ Jacob_0 = \left[\begin{matrix}0 & -5.5 \cdot 10^{-65} & -1.9 \cdot 10^{-32} & 5.0 & 5.0 & 0\\0 & -1.0 & -1.9 \cdot 10^{-32} & -3.1 \cdot 10^{-16} & -1.9 \cdot 10^{-32} & 0\\1.0 & 6.1 \cdot 10^{-17} & -3.1 \cdot 10^{-16} & -5.0 & -9.2 \cdot 10^{-16} & 0\\0 & 0 & -1.0 & 0 & 0 & 0\\0 & 0 & -6.1 \cdot 10^{-17} & -1.0 & -1.0 & -1.0\\0 & 0 & 6.1 \cdot 10^{-17} & 6.1 \cdot 10^{-17} & 6.1 \cdot 10^{-17} & 6.1 \cdot 10^{-17}\end{matrix}\right] \]
奇异
在机器人学中,奇异点是指机器人在特定姿态下失去某些运动自由度的位置。这些特定姿态下,机器人的一个或多个关节速度可能需要无限大,才能产生末端执行器的某个期望速度,这在实际中是不可能的。奇异点的存在对于机器人的控制和操作有重要影响,需要在设计和控制机器人时予以考虑。
当雅可比矩阵的行列式为零时,即表示机器人处于奇异点。这是因为雅可比矩阵不可逆,无法从末端执行器速度计算出关节速度。此时,机器人在某些方向上失去运动能力,即使改变关节速度,末端执行器的速度也不会改变。
雅可比矩阵的矩
要判断一个矩阵的行列式是否为零,可以使用矩阵的秩来进行判断。矩阵的秩是指矩阵中线性无关的行或列的最大数量。如果一个矩阵的秩小于它的维度(行数或列数),则该矩阵的行列式为零。因此我们可以通过雅可比矩阵的秩来快速判断雅可比矩阵是否存在奇异点。
计算过程可以在robot_velocity_jacobian.py中找到。
经过计算,发现该雅可比矩阵的秩为5,说明这说明实际上机器人只有5个自由度。即所有空间都是奇异点。
奇异
然而,分析表明,由于在设计时存在三个在同一平面的轴,故在所有空间内,都有奇异点的存在。或者说对于这个设备,其实际的自由度只能达到5。
\[ det(Jacob_0) = 0 \]
这使得一般的雅可比奇异过程不能再本机构上实现,然后对于一般的机器人的雅可比分析方式依然可以在singularity_analysis.py找到,并且我提供了对另一个机器人——简单改动最后一个轴的方向的机器人的分析。在足够的时间成本下,这个程序可以给出正确的结果.
动力学分析
质量分布
惯性张量是描述刚体对转动的惯性特性的重要量,它与刚体的质量分布和几何形状有关。
在给定坐标系A中,惯性张量的表示可以用一个3x3的矩阵来表示。这个矩阵被称为惯性矩阵或惯性张量矩阵。在这个表达式中,惯性矩阵被表示为一个对称矩阵,对角线上的元素分别表示刚体绕A坐标轴旋转的惯性力矩,非对角线上的元素表示刚体绕A坐标轴旋转的耦合力矩。
\[ { }^A I=\left(\begin{array}{rrr} I_{x x} & -I_{x y} & -I_{x z} \\ -I_{x y} & I_{y y} & -I_{y z} \\ -I_{x z} & -I_{y z} & I_{z z} \end{array}\right) \]
我通过solidwork导出了建模带来的质量分布,如列表如下:
| Mass | Moment Ixx | Moment Ixy | Moment Ixz | Moment Iyy | Moment Iyz | Moment Izz |
|---|---|---|---|---|---|---|
| 23.38782 | 6.425149 | -2.20E-16 | 1.02E-16 | 1.987009 | 5.62E-10 | 4.444118 |
| 9.205307 | 0.470912 | -9.67E-19 | 2.85E-19 | 0.012207 | -7.39E-17 | 0.466974 |
| 1.204045 | 0.000393 | 4.69E-18 | 1.27E-08 | 0.172653 | -2.23E-19 | 0.17265 |
| 0.122888 | 8.09E-05 | -5.39E-13 | -9.25E-20 | 7.28E-05 | 3.22E-20 | 7.17E-05 |
| 1.139717 | 0.000433 | -2.97E-05 | 3.49E-09 | 0.029837 | -1.09E-09 | 0.029969 |
| 0.580515 | 0.012522 | -2.17E-19 | -5.60E-17 | 0.012507 | -6.07E-17 | 0.000275 |
| 0.523966 | 0.00016 | 6.17E-05 | 1.32E-17 | 0.009611 | 1.90E-19 | 0.009736 |
| 0.583844 | 0.00244 | 2.40E-18 | -1.84E-18 | 0.001474 | 0.000566 | 0.00113 |
在程序中添加了质量分布信息的程序可以在Mass_Inertia_Setter.py中找到
动力学分析
在质量信息的基础上,可以进行多样的逆动力学分析方法
逆动力学-递归牛顿欧拉算法
逆动力学是机器人学中的一个重要概念,用于计算机器人在给定关节状态下的关节力和力矩。正向动力学是根据已知的关节力和力矩来计算机器人的运动状态(位置、速度和加速度),而逆动力学则是相反的过程。
逆动力学的计算过程可以通过递归牛顿欧拉算法来实现。该算法从机器人的末端开始,递归地向前和向后传递力和力矩,从而计算出每个关节的力和力矩。递归牛顿欧拉算法利用了牛顿定律和欧拉方程,考虑了机器人的质量、惯性和外部力矩等因素。
相应的代码可以在Mass_Inertia_Setter.py中找到
以下是一些计算结果:
| 关节位置 | 关节速度 | 关节加速度 | 力和力矩-[F_x F_y F_z M_x M_y M_z] | |
|---|---|---|---|---|
| 1 | [0, 0, 0, 0, 0, 0] | [0, 0, 0, 0, 0, 0] | [0, 0, 0, 0, 0, 0] | [ 3.49631265e+02 7.35992828e-15 -8.95879068e-15 -8.43773796e+01 |
| -5.23063684e-15 0.00000000e+00] | ||||
| 2 | [20, 10, pi/3, pi/3, pi/3, pi/3] | [0, 0, 0, 0, 0, 0] | [0, 0, 0, 0, 0, 0] | [ 3.49631265e+02 7.35992828e-15 -8.95879068e-15 -8.43773796e+01 |
| -5.23063684e-15 0.00000000e+00] | ||||
| 3 | [20, 10, pi/3, pi/3, pi/3, pi/3] | [1, 1, 1, 1, 1, 1] | [0, 0, 0, 0, 0, 0] | [ 347.58516689 -250.71837502 21.69095014 -0.91517928 51.59007257 |
| 0. ] | ||||
| 4 | [20, 10, pi/3, pi/3, pi/3, pi/3] | [0, 0, 0, 0, 0, 0] | [1, 1, 1, 1, 1, 1] | [347.20775265 42.27251513 -34.89286925 164.60759118 -16.2169242 |
| 0. ] |
- 通过第1 2 组,可以看到由于没有考虑重力,关节位置并不影响受力
- 通过第3 4组可以看到速度和加速度对系统的影响
关节加速度
accel函数基于逆动力学算法,通过求解动力学方程来计算关节加速度。它考虑了机器人的质量、惯性、连杆参数以及外部力矩的影响。通过使用这个函数,您可以获得机器人在给定关节状态下的加速度信息,从而了解机器人的动力学行为。
然而这触发了由于机器人模型的质量和惯性参数设置不正确导致的异常。这意味着机器人模型的质量和惯性参数无法形成非奇异(非可逆)的惯性矩阵。由于所有的质量信息均由solidwork提供,这是无法解决的。为了继续实验,我使用了Puma560模型进一步实验。
程序可以在puma_exemple.py找到。
| Joint coordinates | Joint velocity | Joint torques of the robot | acceleration due to applied torque | |
|---|---|---|---|---|
| 1 | [0, 0, 0, 0, 0, 0] | [0, 0, 0, 0, 0, 0] | [0, 0, 0, 0, 0, 0] | [ 0.04708838 -8.53721878 4.18541175 5.195206 5.88407268 5.15078362] |
| 2 | [20, 10, pi/3, pi/3, pi/3, pi/3] | [0, 0, 0, 0, 0, 0] | [0, 0, 0, 0, 0, 0] | [-0.46352559 6.19172614 -8.48784377 5.26388791 5.83647604 5.1517202 ] |
| 3 | [0, 0, 0, 0, 0, 0] | [0, 0, 0, 0, 0, 0] | [1, 1, 1, 1, 1, 1] | [ -7.67330515 -12.81640524 -7.87297484 -1.30315941 -0.35232642 |
| 2.4773214 ] | ||||
| 4 | [0, 0, 0, 0, 0, 0] | [1, 1, 1, 1, 1, 1] | [0, 0, 0, 0, 0, 0] | [-2.46226150e-01 -8.68293024e+00 3.14620807e+00 2.09846469e-03 |
| 6.03123947e-02 5.03085045e-05] |
总结
本报告总结了针对武器炮塔装置的机械臂模型的设计和目标。我详细描述了solidwork模型的各个部分及其功能,包括基座、横杆、底座和连杆等。然后,我简化了模型,并使用改进的Denavit-Hartenberg方法重新建立了模型。这一过程包括定义各关节的坐标系,确定原点位置和z轴方向,分析连杆参数,并在Python中进行建模。我对模型进行了运动学分析,计算了机器人手臂的位置和方向。
我还讨论了机器人的运动学分析,包括正向运动学和逆向运动学。正向运动学是根据机器人的关节参数确定其末端执行器位置和姿态的过程。我通过设定关节角度并计算变换矩阵,得到了机器人的正向运动学模型。使用Python的Robotics Toolbox工具箱计算了机器人的正向运动学,验证了之前的分析和计算结果。我还讨论了操作臂子空间,即机器人操作臂在所有可能的关节配置下能够到达的空间区域。操作臂子空间的大小和形状取决于机器人的几何结构,包括关节的数量、类型和排列方式。通过设定关节角度并计算矩阵,我得到了操作臂的子空间矩阵,并对运算过程中的微小偏差进行了讨论。
逆运动学分析是根据机器人末端执行器的位置和姿态计算机器人的关节参数。我使用代数解法和几何解法对逆运动学进行了深入探讨,并尝试了Levenberg-Marquardt方法和Newton-Raphson方法。
我还讨论了机器人的速度和静力学。速度部分介绍了描述关节之间速度和角速度传递的公式,并讨论了速度雅可比矩阵。静力学部分研究了机器人在静止或缓慢移动时受到的力和力矩,这对于设计实现复杂操作的机器人非常重要。我还讨论了机器人学中的奇异点,即机器人在特定姿态下失去某些运动自由度的位置。
最后,我分析了机器人的动力学行为。通过Solidwork导出的质量分布信息和递归牛顿欧拉算法,计算了逆动力学和关节力和力矩。我还使用accel函数计算了关节加速度。
综上所述,本文对武器炮塔装置的机械臂模型进行了设计和分析,并在运动学、逆运动学、速度和静力学以及动力学等方面进行了探讨。


