RDM Chapitre 4 能量方法 Méthodes Energétiques

CSA，CCA，Travail

运动学上可允许的位移场和静力学上可允许的内力场

Champ de déplacement cinématiquement admissible & Champ d’effort intérieur statiquement admissible

• “Champ de déplacement cinématiquement admissible”指的是在物理学，特别是可变形介质力学中，需要找到的一种位移场。这个位移场必须满足一些特定的边界条件，并且具有一定的规则性。这些条件定义了“cinématiquement admissible”的位移场的空间，这个空间包含了所有满足边界条件的足够规则的位移场。记为：

$$[\tilde{\mathrm{U}}]$$

• 同样，“Champ d’effort intérieur statiquement admissible”指的是在物理学，特别是连续介质力学中，需要找到的一种内部应力场。这个应力场必须满足一些特定的边界条件，并且具有一定的规则性。这些条件定义了“statiquement admissible”的内部应力场的空间，这个空间包含了所有满足边界条件的足够规则的内部应力场。记为：

$$[\hat{\mathrm{T}}]$$

给定位移的功和给定力的功

Travail des efforts donnés & Travail des déplacements

$$\mathrm{W}_{\mathrm{f}}^{\mathrm{d}}([\tilde{\mathrm{U}}])=\int([\mathrm{f}] \otimes[\tilde{\mathrm{U}}]) \mathrm{ds}+\left[\mathrm{F}_{\mathrm{k}}\right] \otimes\left[\tilde{\mathrm{U}}\left(\mathrm{s}_{\mathrm{k}}\right)\right] \stackrel{\text { not. }}{=} \tilde{\mathrm{W}}_{\mathrm{f}}^{\mathrm{d}}$$ $$\mathrm{W}_{\mathrm{u}}^{\mathrm{d}}\left(\left[\hat{\mathrm{T}}\right]\right)=\left[\hat{\mathrm{R}}_{\mathrm{A}}\right] \otimes[\mathrm{U}(\mathrm{A})]+\left[\hat{\mathrm{R}}_{\mathrm{k}^{\prime}}\right] \otimes\left[\mathrm{U}\left(\mathrm{s}_{\mathrm{k}^{\prime}}\right)\right] \stackrel{\text { not. }}{=} \hat{\mathrm{W}}_{\mathrm{u}}^{\mathrm{d}}$$

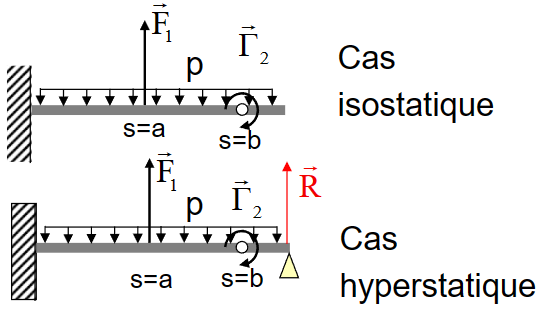
受力平衡和静定性

• 一个静力学上可允许的内力场$[\widehat{\mathrm{T}}(s)]$满足外部和内部平衡条件
• 对于静定系统，唯一的运动学上可允许的位移场就是$CSA$。
• 对于超静定系统，我们需要以线性方式表达所有的未知联接变量，这些变量取决于超静力的未知数。
  • 因此，外部平衡条件得到了满足。
  • 我们可以使用联接变量的表达式来计算内部力矩，这些表达式取决于超静力的未知数。这样，内部平衡条件也得到了满足。
• 设$a_1,…a_h$是超静定的未知数:

$$[\widehat{T}(s)]=\left[\widehat{T}_0(\mathrm{~s})\right]+\sum_1^{\mathrm{h}} \mathrm{a}_{\mathrm{i}}\left[\mathrm{T}_{\mathrm{i}}(\mathrm{s})\right]$$

例子

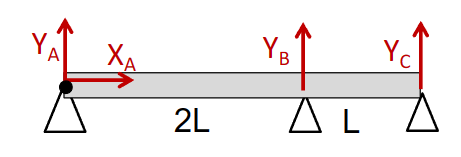
• 图中没有标出的信息：长杆受一个向下的力，其线密度为p
• 平衡方程：

$$\left\{\begin{aligned}& X_A=0 \\& Y_A+Y_B+Y_C-3 p L = 0 \\& 2 Y_B L+3 Y_C L-9 p L^2 / 2 = 0\end{aligned}\right.$$

• 三个方程四个未知数，设$Y_c$为超静定未知数：

$$\begin{aligned}& Y_A=\frac{3 p L}{4}+\frac{Y_C}{2} \\& Y_B=\frac{9 p L}{4}-\frac{3 Y_C}{2}\end{aligned}$$

• 得到一组符合约束条件的CSA

$$S<2 L \quad \left\{\begin{aligned}& R x=0 \\& R y(s)=\frac{3 p L}{4}-p s+\frac{Y_C}{2} \\& M(s)=\frac{p s^2}{2}-\frac{3 p L s}{4}-\frac{Y_C s}{2}\end{aligned}\right.$$ $$S>2 L \quad \left\{\begin{aligned} & R x=0 \\ & R y(s)=3 p L-p s-Y_c \\ & M(s)=\frac{p(3 L-s)^2}{2}-Y_C(3 L-s) \end{aligned}\right.$$

能量方程

能量势定理和互补能量定理

Théorème de l’énergie potentielle & Théorème de l’énergie complémentaire

能量势定理 TEP

• 能量势：

$$\mathrm{U}(\tilde{\mathrm{U}}) \triangleq \frac{1}{2} \int\left\{\mathrm{L}^{-1}(\tilde{D}) \otimes \tilde{D}\right\} \mathrm{ds}-\mathrm{W}_{\mathrm{F}}^{\mathrm{d}}([\tilde{\mathrm{U}}])$$

• 能量势定理：

$$\mathrm{U}(\mathrm{U}) \leq \mathrm{U}(\tilde{\mathrm{U}})$$

在所有运动学上可允许的位移场中，CSA最小化了势能。

互补能量定理 TEC

• 互补能量

$$\mathrm{H}(\hat{\mathrm{T}}) \triangleq \mathrm{W}_{\mathrm{u}}^{\mathrm{d}}\left(\left[\hat{\mathrm{R}}\left(\mathrm{s}_{\mathrm{k}^{\prime}}\right)\right]\right)-\frac{1}{2} \int\left\{\left[\hat{\mathrm{T}}\right] \otimes \mathrm{L}\left(\left[\mathrm{\hat T}\right]\right)\right\} \mathrm{ds}$$

• 互补能量定理

$$\mathrm{H}(\hat{\mathrm{T}}) \leq \mathrm{H} (\mathrm{T})$$

在所有静力学上可允许的内部应力场中，CCA最大限度地增加了互补能量。

梅纳布雷亚定理

对于一个理想约束，约束引入的位移为0

$$\mathrm{W}_{\mathrm{u}}^{\mathrm{d}}\left(\left[\hat{\mathrm{R}}_{\mathrm{k}^{\prime}}\right]\right)=0$$

• 因此互补能量：

$$\mathrm{H}(\hat{\mathrm{T}}) \triangleq -\frac{1}{2} \int\left\{\left[\hat{\mathrm{T}}\right] \otimes \mathrm{L}\left(\left[\mathrm{\hat T}\right]\right)\right\} \mathrm{ds} = -W\left(\left[\hat T\right]\right)$$

• 对于一个h阶超静定系统
  • 静力学方程允许我们根据h个超静定未知数来进行表达$[\hat T]$。
  • 最小化$W[\hat T]$可以得到超静定未知数的值。

梅纳布雷亚定理

• 对于一个无摩擦的约束，应变能量相对于约束的任意一个分量的导数为零

$$\frac{\partial \hat{\mathrm{W}}}{\partial \mathrm{R}_{\mathrm{j}}}=0 \quad \mathrm{j}=\llbracket 1, \mathrm{~h}\rrbracket$$

例子

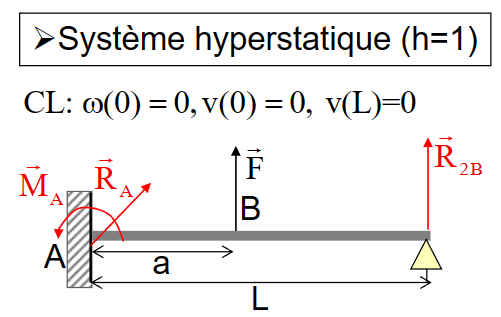
• 注意这里虽然在力学上有一个未知数，但是$v(L) = 0$提供了额外的信息可以求出$R_{2B}$
• 外力平衡

$$R_{1 A}=0 \quad R_{2 A}+R_{2 B}+F=0 \quad M_A+a F+L R_{2 B}=0$$

• 内力

$$\left\{\begin{array}{llll} s<a & N=0 & T_2=-F-R_{2 B} & M_3=-F(a-s)-R_{2 B}(L-s) \\s>a & N=0 & T_2=-R_{2 B} & M_3=-R_{2 B}(L-s) \\\end{array}\right.$$

• 相应的功

$$\mathrm{W}\left(\left[\hat{\mathrm{T}}^{\text {int }}\left(\mathrm{R}_{2 \mathrm{~B}}\right)\right]\right)=\frac{1}{2} \int_0^{\mathrm{L}}\left\{\frac{\mathrm{M}_3^2}{\mathrm{EJ}_2}+\frac{\mathrm{T}_2^2}{\underset{petit}{GS^2}}+\frac{\mathrm{N}^2}{\underset{\mathrm{N}=0}{\mathrm{NS}}}\right\}$$

• 有功对$R_{2B}$的导数：

$$\frac{\mathrm{dW}\left(\left[\hat{\mathrm{T}}\left(\mathrm{R}_{2 \mathrm{~B}}\right)\right]\right)}{\mathrm{dR}_{2 \mathrm{~B}}}=0 \Rightarrow \mathrm{R}_{2 \mathrm{~B}}=\mathrm{F}\left\{\frac{\mathrm{a}^3}{2 \mathrm{~L}^3}-\frac{3}{2} \frac{\mathrm{a}^2}{\mathrm{~L}^2}\right\}$$

麦克斯韦-贝蒂定理和卡斯蒂利亚定理

Théorème de réciprocité(Maxwell-Betti)&Théorème de Castigliano

麦克斯韦-贝蒂/互易定理 TMB

对于任何静定或超静定的弹性系统，如果先施加第一组力，然后在移除后施加第二组力，那么第一组力对于第二组力引起的弹性位移所做的功之和，等于第二组力对于第一组力引起的弹性位移所做的工之和。

$$[T_1][U_2] = [T_2][U_1]$$

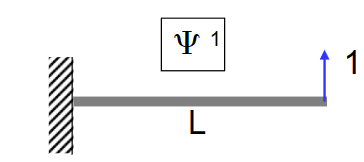
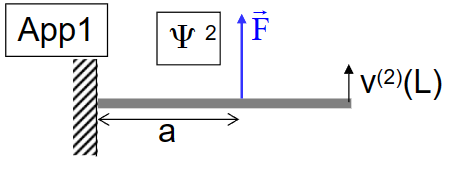
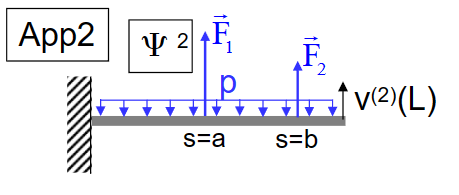
• 在第一幅图中，在杆的由此施加了单位力，其带来的位移：

$$v^{(1)}(s)=\frac{1}{\mathrm{EJ}_2}\left\{\frac{\mathrm{Ls}^2}{2}-\frac{\mathrm{s}^3}{6}\right\}$$

• 在第二幅图中，我们移除了单位力，而施加了新的力$\vec F$，根据TMB，有：

$$1 \cdot v^{(2)}(L)=F \cdot v^{(1)}(a)$$

• 因此得到$v^{(2)}(L)$

$$v^{(2)}(L)=\frac{F}{E_2}\left\{\frac{\mathrm{La}^2}{2}-\frac{a^3}{6}\right\}$$

• 在第三幅图中，引入了一系列的力，根据TMB有：

$$\mathrm{v}^{(2)}(\mathrm{L})=\mathrm{F}_1 \cdot \mathrm{v}^{(1)}(\mathrm{a})+\mathrm{F}_2 \cdot \mathrm{v}^{(1)}(\mathrm{b})-\int_0^{\mathrm{L}} \mathrm{p} \cdot \mathrm{v}^{(1)}(\mathrm{s}) \mathrm{ds}$$

卡斯蒂利亚定理

应变能相对于局部力（扭矩）的导数等于该点和力施加方向上的位移（旋转）

根据卡斯蒂利亚定理：

$$\begin{aligned}& \mathrm{T}(\mathrm{s})=\text { Fonction }\left(\mathrm{p}, \mathrm{F}_1, \mathrm{F}_2, \mathrm{~s}\right) \\& \frac{\partial \mathrm{W}(\mathrm{T})}{\partial \mathrm{F}_1}=\mathrm{v}(\mathrm{a}) \quad \frac{\partial \mathrm{W}(\mathrm{T})}{\partial \mathrm{F}_2}=\omega(\mathrm{b})\end{aligned}$$

同时考虑麦克斯韦-贝蒂定理和卡斯蒂利亚定理

$$\begin{aligned}& \hat{\mathrm{T}}(\mathrm{s})=\text { Fonction }\left(\mathrm{p}, \mathrm{F}_1, \mathrm{F}_2, \mathrm{R}, \mathrm{s}\right) \\& \text { Th.Menabrea } \frac{\partial \mathrm{W}(\hat{\mathrm{T}})}{\partial \mathrm{R}}=0 \rightarrow \mathrm{R} ; \\& \text { en substituant R dans } \mathrm{T} \\& \frac{\partial \mathrm{W}(\mathrm{T})}{\partial \mathrm{F}_1}=\mathrm{v}(\mathrm{a}) \quad \frac{\partial \mathrm{W}(\mathrm{T})}{\partial \mathrm{F}_2}=\omega(\mathrm{b})\end{aligned}$$

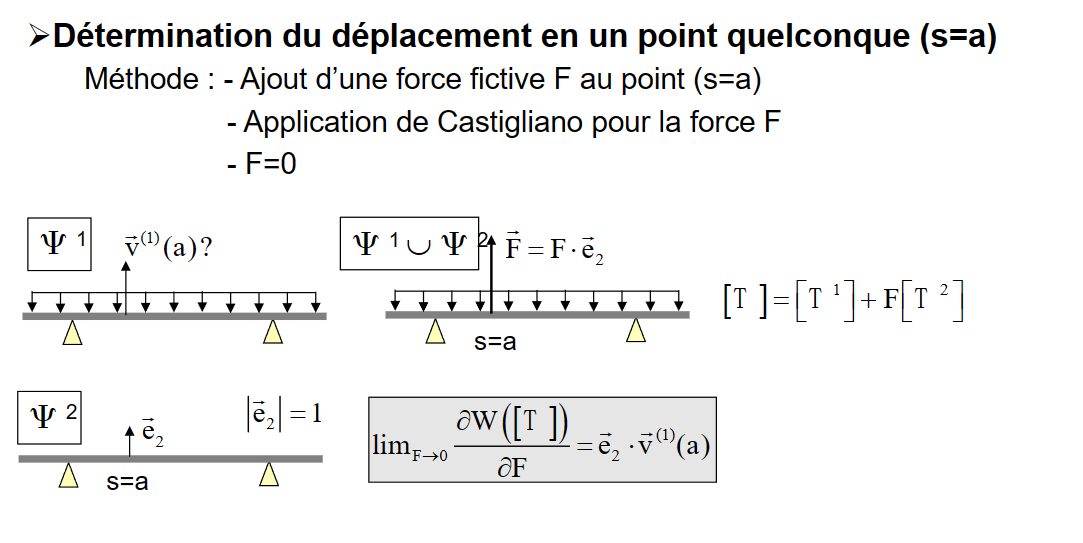
• 求a点位移：
  • 在a点添加一个虚拟力
  • 使用卡斯蒂利亚定理
  • 使F = 0

$$\lim _{\mathrm{F} \rightarrow 0} \frac{\partial \mathrm{W}([\mathrm{T}])}{\partial \mathrm{F}}=\overrightarrow{\mathrm{e}}_2 \cdot \overrightarrow{\mathrm{v}}^{(1)}(\mathrm{a})$$

能量势定理的应用

Application du théorème de l’énergie potentielle

• 假设$[\tilde Ui]$使独立的CCA，则$[\tilde U] = \sum{i = 1}^n\lambda_i[\tilde U_i]$也是一个CCA，如果$[\tilde U_0]$使最小的CCA，则他是$[U]$的最佳近似

矩阵公式

$$\begin{aligned}& \mathrm{W}([\tilde{U}])=\frac{1}{2} \Lambda^{\mathrm{t}} \mathbf{K} \boldsymbol{\Lambda} \quad \boldsymbol{\Lambda}=\left[\begin{array}{c}\lambda_1 \\\vdots \\\lambda_{\mathrm{n}}\end{array}\right] \quad \mathbf{K}: \text { matrice } \mathrm{n} \times \mathrm{n} \\& \mathrm{W}_{\mathrm{F}}^{\mathrm{d}}([\tilde{U}])=\boldsymbol{\Lambda}^{\mathrm{t}} \mathbf{F} \\& \frac{\partial}{\partial \lambda_{\mathrm{i}}}\left\{\mathrm{W}([\tilde{U}])-\mathrm{W}_{\mathrm{f}}^{\mathrm{d}}([\tilde{U}])\right\}=0 \Leftrightarrow \mathbf{K} \boldsymbol{\Lambda}=\mathbf{F}\end{aligned}$$ $$\mathbf{K}_{i j}=\int\left[\tilde{D}_i(\mathrm{~s})\right] \otimes \mathrm{L}^{-1}\left[\tilde{D}_j(\mathrm{~s})\right] \mathrm{ds} \quad \mathbf{F}_i=\mathrm{W}_{\mathrm{u}}^{\mathrm{d}}\left(\left[\tilde{U}_i\right]\right)$$

二维弯曲欧拉-伯努利梁

• 根据欧拉-伯努利假设：

$$\mathrm{v}^{\prime}=\omega \quad \mathrm{M}_{\mathrm{f} 3}=-\mathrm{EJ}_2 \mathrm{v}^{\prime \prime}$$

• 此时的功：

$$\mathrm{W}=\frac{1}{2} \int_0^{\mathrm{L}} \mathrm{EJv}^{\prime \prime 2} \mathrm{ds}$$

• 考虑初始条件：$C L: \quad \mathrm{v}(0)=0 \quad \omega(0)=0 \rightarrow \mathrm{v}^{\prime}(0)=0$
• 满足初始条件的一组CCA：$\text { CCA: } \quad \mathrm{v}_1(\mathrm{~s})=\frac{\mathrm{s}^2}{\mathrm{~L}^2} \quad \mathrm{v}_2(\mathrm{~s})=\frac{\mathrm{s}^3}{\mathrm{~L}^3}$
• 替换为矩阵表达方式：

$$\mathrm{v}_0=\lambda_1 \mathrm{v}_1+\lambda_2 \mathrm{v}_2=\Lambda^{\mathrm{t}} \mathbf{V}=\mathrm{V}^{\mathrm{t}} \Lambda \quad \mathbf{V}=\left[\begin{array}{l}\mathrm{v}_1 \\\mathrm{v}_2\end{array}\right] \Lambda=\left[\begin{array}{l}\lambda_1 \\\lambda_2\end{array}\right]$$

• 其二阶导的平方：

$$\mathrm{v}_0^{\prime \prime}=\Lambda^{\mathrm{t}} \times \mathbf{V}^{\prime \prime} \quad \mathrm{v}_0^{\prime \prime 2}=\Lambda^{\mathrm{t}}\left(\mathbf{V}^{\prime \prime} \mathbf{V}^{\prime \prime} \mathrm{t}\right) \Lambda$$

• 代入能量公式：

$$\tilde{\mathrm{W}}=\frac{1}{2} \int_0^{\mathrm{L}} \mathrm{EJ}_2 \mathrm{v}_0^{\prime \prime 2} \mathrm{ds}=\frac{1}{2} \boldsymbol{\Lambda}^{\mathrm{t}} \underbrace{\left[\int_0^{\mathrm{L}} \mathrm{EJ}_2\left(\mathbf{V}^{\prime \prime} \times \mathbf{V}^{\prime \prime t}\right) \mathrm{ds}\right]}_{\mathbf{K}} \boldsymbol{\Lambda}$$

• 得到K：

$$\mathbf{K}=\mathrm{EJ}_2\left[\begin{array}{ll}\int_0^{\mathrm{L}} \mathrm{v}_1^{\prime \prime 2} & \int_0^{\mathrm{L}} \mathrm{v}_1^{\prime \prime} \mathrm{v}_2^{\prime \prime} \\(s y m) & \int_0^{\mathrm{L}} \mathrm{v}_2^{\prime \prime 2}\end{array}\right]\mathbf{K}=\frac{\mathrm{EJ}_2}{\mathrm{~L}^3}\left[\begin{array}{cc} 4 & 6 \\ 6 & 12 \end{array}\right]$$