RDM Chapitre 3 变形，本构关系 Déformation, loi de comportement

位移和形变

位移螺旋 Torseur de déplacement

• 对于等投影场：$\overrightarrow{\mathrm{V}}{\mathrm{P}}=\overrightarrow{\mathrm{V}}{\mathrm{G}}+\vec{\Omega} \wedge \overrightarrow{\mathrm{GP}}$ ，则有速度螺旋分布：

$$\left[\mathrm{V}_{\Sigma}\right]=\left| \begin{aligned}& \vec{\Omega} \\& \vec{V}_{\mathrm{G}}\end{aligned}\right.$$

• 一般来说，对于非刚体的结构的位移场不是等投影的，对于微小位移和微小旋转，定义位移螺旋分布：

$$\left[\mathrm{U}_{\Sigma}\right]=\left | \begin{aligned}&\vec \omega\\&\vec u_G\end{aligned}\right.$$

形变螺旋 Torseur de déformation

• 形变螺旋定义为位移螺旋对$s$的微分：

$$[D]_{\Sigma}=\frac{\mathrm{d}[\mathrm{U}]_{\Sigma}}{\mathrm{ds}}= \left|\begin{aligned} & \frac{\mathrm{d} \vec{\omega}}{\mathrm{ds}} \triangleq \vec{\chi}(\mathrm{s}) \\ & \frac{\mathrm{d} \overrightarrow{\mathrm{u}}}{\mathrm{ds}}+\overrightarrow{\mathrm{x}}_1 \wedge \vec{\omega} \triangleq \vec{\varepsilon}(\mathrm{s}) \end{aligned}\right.$$

形变螺旋的分解

• torsion 扭转
• $\chi_1=\overrightarrow{\mathrm{x}}_1 \cdot \vec{\chi}$
• flexion 屈曲
• $\chi{\mathrm{j}}=\overrightarrow{\mathrm{x}}{\mathrm{j}} \cdot \vec{\chi}_{(\mathrm{j}=2,3)}$

• allongement 拉伸
• $\varepsilon_1=\vec{x}_1 \cdot \vec{\varepsilon}$
• glissement 滑移
• $\varepsilon{\mathrm{j}}=\overrightarrow{\mathrm{x}}{\mathrm{j}} \cdot \vec{\varepsilon}_{(\mathrm{j}=2,3)}$

本征关系

$$\left[\begin{array}{l}\varepsilon_1 \\\chi_2 \\\chi_3 \\\chi_1 \\\varepsilon_2 \\\varepsilon_3\end{array}\right]=-\left[\begin{array}{llllll}1 / \mathrm{ES} & 0 & 0 & 0 & 0 & 0 \\0 & 1 / \mathrm{EJ}_3 & 0 & 0 & 0 & 0 \\0 & 0 & 1 / \mathrm{EJ}_2 & 0 & 0 & 0 \\0 & 0 & 0 & 1 / \mathrm{GI} & 0 & 0 \\0 & 0 & 0 & 0 & 1 / \mathrm{GS}_2 & 0 \\0 & 0 & 0 & 0 & 0 & 1 / \mathrm{GS}\end{array}\right]\left[\begin{array}{c}\mathrm{N} \\\mathrm{M}_2 \\\mathrm{M}_3 \\\mathrm{M}_{\mathrm{t}} \\\mathrm{T}_2 \\\mathrm{~T}\end{array}\right]$$

• 其中：

$$\frac{1}{\mathrm{~S}_{\mathrm{j}}}=\frac{1}{\mathrm{~J}_{\mathrm{j}}^2} \int_{\Sigma} \frac{\left\{\mu_{\mathrm{j}}\left(\mathrm{x}_{\mathrm{j}}\right)\right\}^2}{\left\{\mathrm{~b}\left(\mathrm{x}_{\mathrm{j}}\right)\right\}^2} \mathrm{dS}$$

• 对于矩形：$S_j=\frac{5}{6} S$
• 对于圆形：$S_j=\frac{9}{10} S$

能量关系

功

$$\mathrm{w}^{\mathrm{RDM}}=-\frac{1}{2}[\mathrm{~T}(\mathrm{~s})] \otimes[D(\mathrm{~s})]=\frac{1}{2}[\mathrm{~T}(\mathrm{~s})] \otimes \mathrm{L}[\mathrm{T}(\mathrm{s})]=\frac{1}{2}[D(\mathrm{~s})] \otimes \mathrm{L}^{-1}[D(\mathrm{~s})]$$

使用外力表示

$$\mathrm{w}(\mathrm{T})=\frac{1}{2}\left\{\frac{\mathrm{N}^2}{\mathrm{ES}}+\frac{\mathrm{M}_{\mathrm{f} 3}^2}{\mathrm{EJ}_2}+\frac{\mathrm{M}_{\mathrm{f} 2}^2}{\mathrm{EJ}_3}+\frac{\mathrm{M}_{\mathrm{t}}^2}{\mathrm{GI}}+\frac{\mathrm{T}_2^2}{\mathrm{GS}_2}+\frac{\mathrm{T}_3^2}{\mathrm{GS}_3}\right\}$$

使用形变表示

$$\mathrm{w}(D)=\frac{1}{2}\left\{\mathrm{ES} \varepsilon_1^2+\mathrm{EJ}_2 \chi_3^2+\mathrm{EJ}_3 \chi_2^2+\mathrm{GI}_1^2+\mathrm{GS}_2 \varepsilon_2^2+\mathrm{GS}_3 \varepsilon_3^2\right\}$$

符号

符号	中文名称	法语名称	公式
$E$	弹性模量	module d’élasticité
$G$	剪切模量	module de cisaillemen t	$\mathrm{G}=\mathrm{E} / 2(1+v)$
$S$	截面面积	aire de Σ
$J_i$	转动惯量	inertie principale de section	$\mathrm{J}{\mathrm{i}}=\int{\Sigma} \mathrm{x}_{\mathrm{i}}^2 \mathrm{dS}$
$S_j$	缩放面积	aire de section réduite	$\frac{1}{\mathrm{~S}{\mathrm{i}}} \simeq \frac{1}{\mathrm{~J}{\mathrm{i}}^2} \int{\Sigma}\left{\frac{\mu{\mathrm{i}}\left(\mathrm{x}{\mathrm{i}}\right)}{\mathrm{b}\left(\mathrm{x}{\mathrm{i}}\right)}\right}^2 \mathrm{dx}_2 \mathrm{dx}_3$
$I$	扭转惯量	inertie de torsion de $\Sigma$	$\mathrm{I}=2 \int_{\Sigma} \Phi \mathrm{dx}_2 \mathrm{dx}_3$

假设和化简

欧拉-伯努利假设

$$\varepsilon_i=0 \text { et } \frac{T_j^2}{G S_j}=0 \quad j=2,3$$

• 忽略滑移项

$$\begin{aligned}& \mathrm{w}(\mathrm{T})=\frac{1}{2}\left\{\frac{\mathrm{N}^2}{\mathrm{ES}}+\frac{\mathrm{M}_3^2}{\mathrm{EJ}_2}+\frac{\mathrm{M}_2^2}{\mathrm{EJ}_3}+\frac{\mathrm{M}_{\mathrm{t}}^2}{\mathrm{GI}}\right\} \\& \mathrm{w}(D)=\frac{1}{2}\left\{\mathrm{ES}_1^2+\mathrm{EJ}_2 \chi_3^2+\mathrm{EJ}_3 \chi_2^2+\mathrm{GI} \chi_1^2\right\}\end{aligned}$$

平面问题

$$\begin{aligned} & \mathrm{w}(\mathrm{T})=\frac{1}{2}\left\{\frac{\mathrm{N}^2}{\mathrm{ES}}+\frac{\mathrm{M}_3^2}{\mathrm{EJ}_2}+\frac{\mathrm{T}_2^2}{\mathrm{GS}_2}\right\} \\ & \mathrm{w}(D)=\frac{1}{2}\left\{\mathrm{ES} \varepsilon_1^2+\mathrm{EJ}_2 \chi_3^2+\mathrm{GS} _ 2 \varepsilon_2^2\right\} \end{aligned}$$

线性问题：直梁

$$\mathrm{w}(D)=\frac{1}{2}\left\{\mathrm{ESu}^{\prime 2}+\mathrm{EJ}_2 \omega^{\prime 2}+\mathrm{GS}_2\left(\mathrm{v}^{\prime}-\omega\right)^2\right\}$$

解题方法

$$[D]_{\Sigma}=\frac{\mathrm{d}[\mathrm{U}]_{\Sigma}}{\mathrm{ds}}= \left|\begin{aligned} & \frac{\mathrm{d} \vec{\omega}}{\mathrm{ds}} \triangleq \vec{\chi}(\mathrm{s}) \\ & \frac{\mathrm{d} \overrightarrow{\mathrm{u}}}{\mathrm{ds}}+\overrightarrow{\mathrm{x}}_1 \wedge \vec{\omega} \triangleq \vec{\varepsilon}(\mathrm{s}) \end{aligned}\right.$$ $$\frac{\mathrm{d}[\mathrm{U}]}{\mathrm{ds}}=-\mathrm{L}[\mathrm{T}(\mathrm{s})]$$

一般平面问题

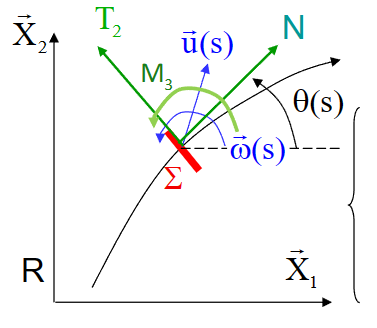
为了计算形变，我们应该首先知道速度向量和角速度向量，同时研究$\vec{x}_1 \wedge \vec{\omega}$

曲梁

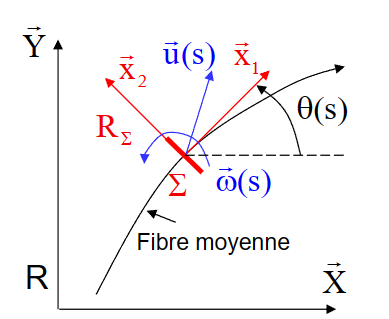
1. $\vec{u}(s)=u \vec{X}+v \vec{Y}$
2. $\vec{\omega}(s)=\omega \vec{X}_3=\omega \vec{x}_3$
3. $\vec{x}_1 \wedge \vec{\omega}=\vec{x}_1 \wedge \omega \vec{x}_3=-\omega \vec{x}_2$

• 注意从地面坐标系$(\vec X, \vec Y)$转换到截面坐标系$(\vec x_1, \vec x_2)$

$\frac{d \vec{u}}{d s}=u^{\prime} \vec{X}+v^{\prime} \vec{Y}=\left(u^{\prime} \cos \theta+v^{\prime} \sin \theta\right) \vec{x}_1+\left(-u^{\prime} \sin \theta+v^{\prime} \cos \theta\right) \vec{x}_2$

• 得到：

$$\left|\begin{aligned}& \chi_3=\omega^{\prime} \\& \varepsilon_1=u^{\prime} \cos \theta+v^{\prime} \sin \theta \\& \varepsilon_2=-u^{\prime} \sin \theta+v^{\prime} \cos \theta-\omega\end{aligned}\right.$$

考虑与外力的联系

$$\left.\begin{array}{l}\chi_3=\omega^{\prime}=-\frac{M_3(s)}{E J_2} \\\varepsilon_1=u^{\prime} \cos \theta+v^{\prime} \sin \theta=-\frac{N(s)}{E S} \\\varepsilon_2=-u^{\prime} \sin \theta+v^{\prime} \cos \theta-\omega=-\frac{T_2(s)}{G S_2}\end{array}\right\}$$

直梁

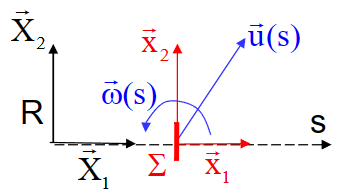
1. $\vec u = u\vec X+v\vec Y= u \vec x_1+v\vec x_2$
2. $\vec \omega = \omega\vec x_3$
3. $\vec x_1\wedge\vec \omega = -\omega\vec x_2$

• 得到：

$$\left |\begin{aligned}& \chi_3=\omega^{\prime} \\& \varepsilon_1=\mathrm{u}^{\prime} \\& \varepsilon_2=\mathrm{v}^{\prime}-\omega\end{aligned}\right.$$

考虑与外力的关系

$$\begin{aligned}& \omega^{\prime}=-\frac{\mathrm{M}_{\mathrm{f} 3}}{\mathrm{EJ}_2} \\&\mathrm{u}^{\prime}=-\frac{\mathrm{N}}{\mathrm{ES}} \\& \mathrm{v}^{\prime}-\omega=-\frac{\mathrm{T}_2}{\mathrm{GS}_2}\end{aligned}$$

孤立系统的解题思路

• 根据超静定未知数 ，计算约束力
• 计算内部力 $[T (s,R_k)]$
• 解微分方程系统 ：$\frac{\mathrm{d}[\mathrm{U}]}{\mathrm{ds}}=-\mathrm{L}[\mathrm{T}(\mathrm{s})]$
• 通过强制实施联接的运动条件 (除了与超静定未知数相关的情况) 和一根梁上的位移和旋转的连续性，来计算积分常数
• 得到的位移场依赖于 h 个未知数：$[U(s,Rk)]$
• 通过将以前忽略的 h 个 CCL 应用于 $[U(s,Rk)]$，我们得到一个系统，该系统由 h 个等式组成，可以计算 h 个约束未知数和位移场 $[U(s)]$

静定问题 - 以直杆为例

静定问题 - 单一外力

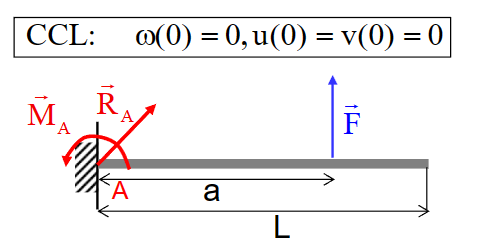
1. 研究静定性：该结构只受固支约束，因此有三个未知数，同时单杆结构对应三个方程，方程数量与未知数数量相等，因此，该问题是静定问题
2. 研究外力平衡：

$$\left\{\begin{aligned}&R_{A,x} = 0\\&R_{A,y}+F = 0\\&M_A+aF = 0\end{aligned}\right.$$

1. 研究内力：
   • 由于左端受力比右端复杂许多，从右端开始研究
   • 注意这里的方向问题，因为是从右向左研究，所以积分后要加负号
   • 当$a<s<L$，系统不受任何力和力矩作用，有：$\begin{array}{llll} \mathrm{N}=0 & \mathrm{~T}2=0 & \mathrm{M}{\mathrm{f} 3}=0\end{array}$
   • 当$0<s<a$，系统只受$\vec F$一个力的作用，有：$N=0 \quad T2=-F \quad M{f 3}=-F(a-s)$

2. 研究形变和内力的关系：

   • 首先研究角加速度：

     $$\chi_3=\omega^{\prime}=-\frac{M_3(s)}{EJ_2} = \left\{\begin{aligned}&\frac{F(a-s)}{EJ_2}&0<s<a\\&0&a<s<l\end{aligned}\right.$$

   • 然后积分得到角速度：

     $$\omega = \int\omega^{\prime}ds = \left\{\begin{aligned}&\int^a_0\omega^{\prime}ds = \frac{F}{EJ_2}\left\{as-\frac{s^2}{2}\right\}+\omega(0) = \frac{F}{EJ_2}\left\{as-\frac{s^2}{2}\right\}\\&\int^L_a0ds = \omega(a) = \frac{Fa^2}{2EJ_2}\end{aligned}\right.$$

   • 然后研究加速度的分量，考虑欧拉-伯努利假设：

     $$\begin{aligned}&u^{\prime} = \varepsilon_1 = -\frac{N(s)}{ES} = 0\\&v^{\prime}-\omega = -\frac{T_2}{GS_2} = 0\end{aligned}$$

   • 得到速度的切向分量：

     $$v= \left\{\begin{aligned}&v(0)+\frac{\mathrm{F}}{\mathrm{EJ}_2}\left\{\frac{\mathrm{as}^2}{2}-\frac{\mathrm{s}^3}{6}\right\}&0<s<a\\&v(a)+\omega(a) \cdot(s-a)=\frac{F}{E J_2}\left\{-\frac{a^3}{6}+\frac{a^2 s}{2}\right\}&a<s<L\end{aligned}\right.$$

静定问题-两个外力的叠加

• 该结构受两个独立的外力，可以分别计算两个受力带来的形变，然后使用叠加原理相加即可：
• 对于第一个力

$$\begin{array}{ll}\mathrm{s}<\mathrm{a} & \mathrm{v}^{(1)}=\frac{\mathrm{F}^{(1)}}{\mathrm{EJ}_2}\left\{\frac{\mathrm{as}^2}{2}-\frac{\mathrm{s}^3}{6}\right\} \\\mathrm{s}>\mathrm{a} & \mathrm{v}^{(1)}=\frac{\mathrm{F}^{(1)}}{\mathrm{EJ}_2}\left\{-\frac{\mathrm{a}^3}{6}+\frac{\mathrm{a}^2 \mathrm{~s}}{2}\right\}\end{array}$$

• 对于第二个力

  $$\mathrm{a}=\mathrm{L} \rightarrow \mathrm{v}^{(2)}=\frac{\mathrm{F}^{(2)}}{\mathrm{EJ}_2}\left\{\frac{\mathrm{Ls}^2}{2}-\frac{\mathrm{s}^3}{6}\right\}$$

• 叠加：

  $$\begin{aligned} & \mathrm{v}(\mathrm{s})=\mathrm{v}^{(1)}(\mathrm{s})+\mathrm{v}^{(2)}(\mathrm{s}) \\ & \mathrm{v}(\mathrm{L})=\frac{\mathrm{F}^{(1)}}{\mathrm{EJ}_2}\left\{-\frac{\mathrm{a}^3}{6}+\frac{\mathrm{a}^2 L}{2}\right\}+\frac{\mathrm{F}^{(2)}}{\mathrm{EJ}_2} \frac{\mathrm{L}^3}{3} \end{aligned}$$

超静定问题 - 以直杆为例

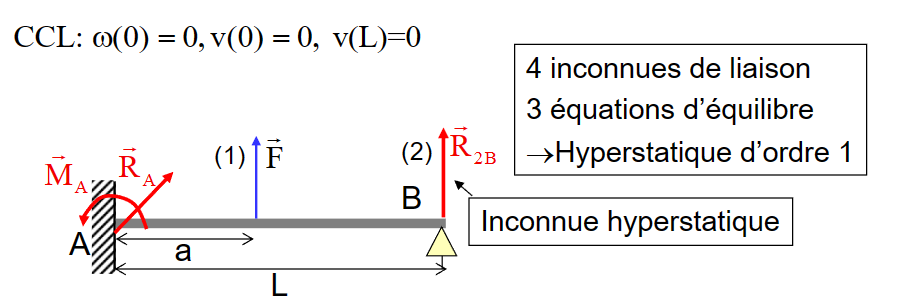
• 该题目有两处约束：固支和点支撑，共计四个未知数，而共计三个方程，因此，这是一道超静定的问题。

计算位移

• 计算在这种情况下的位移：
• 具体的计算过程如下，整体的思想与之前相同，不再过多描述
• 外力平衡

$$\left\{\begin{array}{l}R_{A \cdot x}=0 \\R_{A \cdot y}+F_1+R_{2 B}=0 \\a F_1+L \cdot R_{2 B}+M_A=0\end{array}\right.$$

• 分别讨论$F1$和$R{2B}$

$$\left\{\begin{array}{l}N=0 \\T_2=-R_{2 B} \\M_{3 f}=-(L-S) \cdot R_{2 B}\end{array}\right.$$ $$\left\{\begin{array} { l } { N = 0 } \\ { T _ { 2 } = - F _ { 1 } \quad } \\ { M _ { 3 } f = - ( a - s ) F _ { 1 } } \end{array} \quad \left\{\begin{array}{l} N=0 \\ T_2=0 \\ M_{3 f}=0 \end{array}\right.\right.$$

• $R_{2B}$引入的形变

$$\begin{aligned}& w^{\prime}=\frac{-M_{3 f}}{E J_2}=\frac{(L-S) R_{2 B}}{E J_2} \\& w=\frac{R_{2 B}}{E J_2}\left(L S-\frac{1}{2} S^2\right)+w(0) \\& v^{\prime}=w \\& v=\frac{R_{2 B}}{E J_2}\left(\frac{1}{2}Ls^2-\frac{1}{6} s^3\right)\end{aligned}$$

• $F$引入的形变

$$\begin{aligned} & w_{[0, a]}^{\prime}=\frac{(a-s)}{E J_2} F_1 \\ & \omega_{[0, a]}=\frac{F_1}{E J_2}\left(a s-\frac{1}{2} s^2\right) \\ & v_{[0, a]}=\frac{F_1}{E J_2}\left(\frac 12 a s^2-\frac{1}{b} s^3\right) \\ & v_{[a, L]}=v(a)+w(a)(s-a) =\frac{F_1}{E J_2}\left(-\frac{a^3}{6}+\frac{a^2 s}{2}\right) \end{aligned}$$

• 叠加$L$处的形变

$$\mathrm{v}(\mathrm{L})=\frac{\mathrm{F}}{\mathrm{EJ}_2}\left\{-\frac{\mathrm{a}^3}{6}+\frac{\mathrm{a}^2 \mathrm{~L}}{2}\right\}+\frac{\mathrm{R}_{2 \mathrm{~B}}}{\mathrm{EJ}_2} \frac{\mathrm{L}^3}{3}$$

假设$v(L) = 0$

$$\mathrm{v}(\mathrm{L})=0 \Rightarrow \mathrm{R}_{2 \mathrm{~B}}=\mathrm{F}\left\{\frac{\mathrm{a}^3}{2 \mathrm{~L}^3}-\frac{3}{2} \frac{\mathrm{a}^2}{\mathrm{~L}^2}\right\}$$

假设存在微小位移$v(L) = 0$

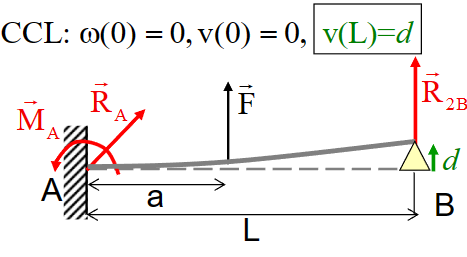
$$\begin{aligned}\mathrm{v}(\mathrm{L})=d \Rightarrow & \mathrm{R}_{2 \mathrm{~B}}=\mathrm{F}\left\{\frac{\mathrm{a}^3}{2 \mathrm{~L}^3}-\frac{3}{2} \frac{\mathrm{a}^2}{\mathrm{~L}^2}\right\}+\frac{3 \mathrm{EJ}_2}{\mathrm{~L}^3} d \\\mathrm{R}_{2 \mathrm{~B}} & =\mathrm{R}_{2 \mathrm{~B}}^{(d=0)}+\frac{3 \mathrm{EJ}_2}{\mathrm{~L}^3} d\end{aligned}$$

假设点支撑为弹簧

• 位移方程不变

$$\mathrm{v}(\mathrm{L})=\frac{\mathrm{F}}{\mathrm{EJ}_2}\left\{-\frac{\mathrm{a}^3}{6}+\frac{\mathrm{a}^2 \mathrm{~L}}{2}\right\}+\frac{\mathrm{F}^{(\mathrm{k})}}{\mathrm{EJ}_2} \frac{\mathrm{L}^3}{3}$$

• 代入弹簧弹力方程

$$\frac{F^{(k)}}{-k}=\frac{F}{EJ_2}\left\{-\frac{a^3}{6}+\frac{a^2 ~L}{2}\right\}+\frac{F^{(k)}}{EJ_2} \frac{L^3}{3}$$

• 整理得：

$$\mathrm{F}^{(\mathrm{k})}\left(1+\frac{3 \mathrm{EJ}_2}{\mathrm{~kL}^3}\right)=\mathrm{F}\left\{\frac{\mathrm{a}^3}{2 \mathrm{~L}^3}-\frac{3 \mathrm{a}^2}{2 \mathrm{~L}^2}\right\}\\\Rightarrow\mathrm{F}^{(\mathrm{k})}=\frac{1}{\left(1+\frac{3 \mathrm{EJ}_2}{\mathrm{~kL}^3}\right)} \mathrm{R}_{2 \mathrm{~B}}^{\mathrm{k}=\infty}$$