RDM Chapitre 2 量化应力 Dimensionnement Contrainte
RDM Chapitre 2 量化应力 Dimensionnement Contrainte
圣韦南假设
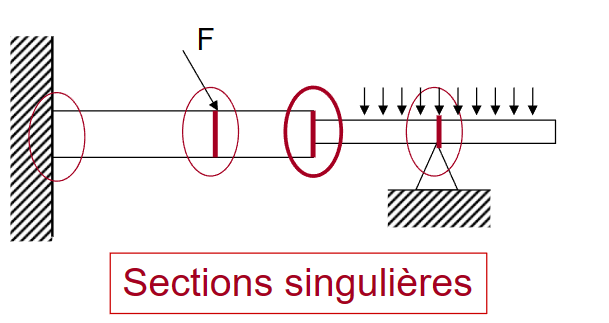
- 奇异截面 Sections singulières 之外,应力 contraintes 只和内力相关
圣韦南问题
假设:
- 横截面恒定的直梁
- 同质弹性各向同性材料
- 载荷:\(\Sigma_1\)上的扭矩\([F]\),\(\Sigma_1\)上的\([F_0]\),\([F]+[F_0]=[0]\)
- SL上没有载荷
目标:
- 定义一个静态可接受的\(σ(P)\)场,满足应力的兼容性方程(Beltrami)
应力
\[ \sigma(\mathrm{P})=\left[\begin{array}{ccc}\sigma_{11} & \sigma_{12} & \sigma_{13} \\\sigma_{12} & 0 & 0 \\\sigma_{13} & 0 & 0\end{array}\right] \]
- 正应力:\(\sigma_{\mathrm{n}}=\sigma_{11}\)
- 切应力:\(\vec{\tau}=\sigma_{12} \vec{x}_2+\sigma_{13} \vec{x}_3\)
应力的方程
\[ \left\{\begin{align}&{l}\sigma_{\mathrm{ij}, \mathrm{j}}=0 \\&\sigma_{\mathrm{ij}, 11}+\frac{1}{1+v} \sigma_{\mathrm{kk}, \mathrm{ij}}=0 \\&\sigma_{\mathrm{ij}} \mathrm{n}_{\mathrm{j}} \mid \Sigma_{\mathrm{L}}=0\end{align}\right. \]
(1)局部平衡方程 Equation d’équilibre local (pas de force de volume)
(2)应力完备性条件 Equation de compatibilité en contrainte(Beltrami)
(3)边界条件 Conditions aux limites
\[ \left\{\begin{align*} { \int _ { \Sigma _ { 1 } } \sigma _ { 1 1 } \mathrm { dS } = \mathrm { F } _ { 1 } } \\{ \int _ { \Sigma _ { 1 } } \sigma _ { 1 2 } \mathrm { dS } = \mathrm { F } _ { 2 } } \\{ \int _ { \Sigma _ { 1 } } \sigma _ { 1 3 } \mathrm { dS } = \mathrm { F } _ { 3 } }\end{align*} \quad \quad \left\{\begin{align*}&\int_{\Sigma_1}\left(\mathrm{x}_2 \sigma_{13}-\mathrm{x}_3 \sigma_{12}\right) \mathrm{dS}=\mathrm{M}_1 \\&\int_{\Sigma_1} \mathrm{x}_3 \sigma_{11} \mathrm{~d} S=\mathrm{M}_2 \\&-\int_{\Sigma_1} \mathrm{x}_2 \sigma_{11} \mathrm{dS}=\mathrm{M}_3\end{align*}\right.\right. \]
应力与内力的联系
正应力
与外力的联系
\[ \sigma_{11}=\frac{F_1}{S}-\frac{M_3}{J_2} x_2+\frac{M_2}{J_3} x_3-\frac{F_2\left(L-x_1\right) x_2}{J_2}-\frac{F_3\left(L-x_1\right) x_3}{J_3} \]
\[ J_i = \int x_i^2dS \]
转化到与内力的联系-在梁模型条件下
- 外力与内力的联系
\[ \begin{gathered}N\left(x_1\right)=-F_1 \\M_{f 2}\left(x_1\right)=-M_2+\left(L-x_1\right) F_3 \\M_{f 3}\left(x_1\right)=-M_3+\left(L-x_1\right) F_2\end{gathered} \]
- 得到应力与内力的联系:
\[ \sigma_{11}\left(\mathrm{~s}, \mathrm{x}_2, \mathrm{x}_3\right)=-\frac{\mathrm{N}(\mathrm{s})}{\mathrm{S}}+\frac{\mathrm{M}_{\mathrm{f} 3}(\mathrm{~s})}{\mathrm{J}_2} \mathrm{x}_2-\frac{\mathrm{M}_{\mathrm{f} 2}(\mathrm{~s})}{\mathrm{J}_3} \mathrm{x}_3 \]
正应力的分解
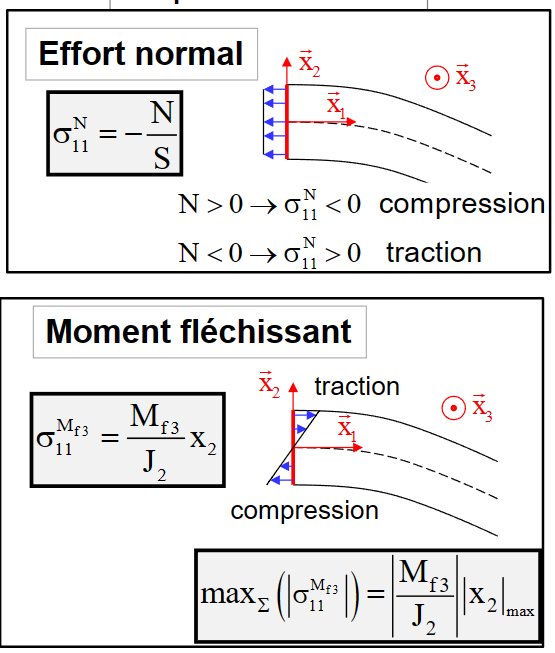
轴力
- 压缩或拉伸
弯矩
- 部分拉伸部分压缩
最大弯矩:
\[ \max _{\Sigma}\left(\left|\sigma_{11}^{\mathrm{M}_{\mathrm{f} 3}}\right|\right)=\left|\frac{\mathrm{M}_{\mathrm{f} 3}}{\mathrm{~J}_2}\right|\left|\mathrm{x}_2\right|_{\max } \]
数量级关系
\[ \frac{\sigma_{11}^{\mathrm{N}}}{\sigma_{11 \max }^{\mathrm{M}_{\mathrm{f}}}} \approx \frac{d}{L} \]
切应力 - 受扭矩的情况
切应力与扭矩的关系
\[ \sigma_{12}\left(\mathrm{x}_2, \mathrm{x}_3\right)=\frac{\mathrm{M}_1}{\mathrm{I}} \frac{\partial \Phi}{\partial \mathrm{x}_3} \quad \sigma_{13}\left(\mathrm{x}_2, \mathrm{x}_3\right)=-\frac{\mathrm{M}_1}{\mathrm{I}} \frac{\partial \Phi}{\partial \mathrm{x}_2} \]
- 其中\(\Phi\)是一个标量函数
切应力与内力的关系
\[ \sigma_{12}\left(\mathrm{x}_2, \mathrm{x}_3\right)=-\frac{\mathrm{M}_t}{\mathrm{I}} \frac{\partial \Phi}{\partial \mathrm{x}_3} \quad \sigma_{13}\left(\mathrm{x}_2, \mathrm{x}_3\right)=\frac{\mathrm{M}_t}{\mathrm{I}} \frac{\partial \Phi}{\partial \mathrm{x}_2} \]
切应力的合成
- 切应力的合成:\(\tau = \sigma_{12}\vec e_2+\sigma_{13}\vec e_3\)
以圆和圆环为例
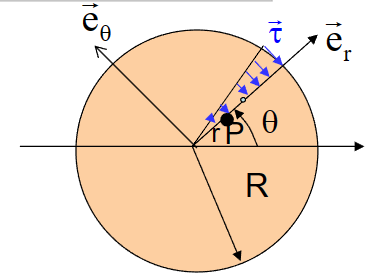
对于圆的情况
\(\Phi(r,\theta) = \frac 12(R^2-r^2)\)
\(I = 2\int_{\Sigma}\Phi \ rd\theta dr = \frac {\pi R^4}2\)
其切应力:
\(\sigma_{12} = -\frac{M_t}{\pi R^4/2}\cdot0\)
\(\sigma_{13} = \frac{M_t}{\pi R^4/2} \cdot -r\)
- 这里需注意柱坐标系中,\(\vec e_z\)为\(\vec x_1\)的方向,\(\vec e_r \sim \vec x_2, \ \ \vec e_\theta \sim \vec x_3\)
得到切应力的最大值:\(|\vec{\tau}|_{\max }=\left|M_t\right|^* \frac{2}{\pi R^3}\)
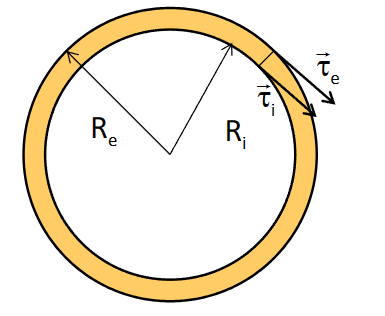
对于圆环的情况
\(\Phi(r,\theta) = \frac 12(R^2-r^2)\)
\(I = 2\int_{R_i}^{R_e}\Phi \ rd\theta dr = \frac {\pi( R_e^4-R_i^4)}2\)
其切应力:\(\sigma_{1 \mathrm{r}}=0 \quad \sigma_{1 \theta}=-\frac{\mathrm{M}_{\mathrm{t}}}{\mathrm{I}} \mathrm{r}\)
切应力的最大值:\(|\vec{\tau}|_{\max }=M_t\cdot \frac{2 R_e}{\pi\left(R_e^4-R_i^4\right)}\)
数量级关系
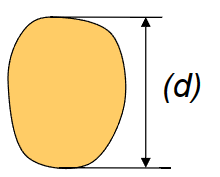
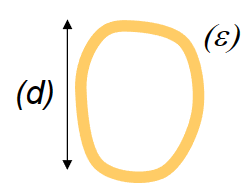
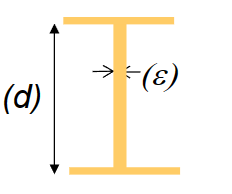
\[ \begin{array}{l|r|l} \mathrm{I} \approx \mathrm{d}^4 \mathrm{~A} \approx \mathrm{d}^2 & \mathrm{I} \approx \varepsilon \mathrm{d}^3 \mathrm{~A} \approx \varepsilon \mathrm{d} & \mathrm{I} \approx \varepsilon^3 \mathrm{~d} \quad \mathrm{~A} \approx \varepsilon \mathrm{d} \\ \tau_{\max } \approx \frac{F L}{d A} & \tau_{\max } \approx \frac{F L}{d A} & \tau_{\max } \approx \frac{F L}{\varepsilon A} \end{array} \]
切应力 - 受剪力的情况
切应力与剪力的关系
\[ \int_{\Gamma} \underbrace{\left(\sigma_{12} \mathrm{n}_2+\sigma_{13} \mathrm{n}_3\right)}_{\vec{\tau} \cdot \overrightarrow{\mathrm{n}}} \mathrm{d} \lambda=\frac{\mathrm{T}_2}{\mathrm{~J}_2} \mu_2(\Gamma)+\frac{\mathrm{T}_3}{\mathrm{~J}_3} \mu_3(\Gamma) \]
- 分解:
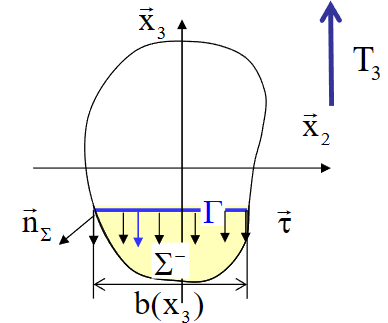
\[ \begin{aligned}\sigma_{13}^{\mathrm{T}_3} & =\frac{\mathrm{T}_3}{\mathrm{~J}_3} \frac{\mu_3\left(\mathrm{x}_3\right)}{\mathrm{b}\left(\mathrm{x}_3\right)} \\\sigma_{12}^{\mathrm{T}_3} & =0\end{aligned} \]
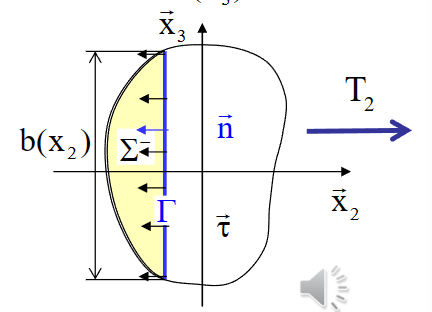
\[ \begin{aligned}\sigma_{12}^{\mathrm{T}_2} & =\frac{\mathrm{T}_2}{\mathrm{~J}_2} \frac{\mu_2\left(\mathrm{x}_2\right)}{\mathrm{b}\left(\mathrm{x}_2\right)} \\\sigma_{13}^{\mathrm{T}_2} & =0\end{aligned} \]
以矩形为例
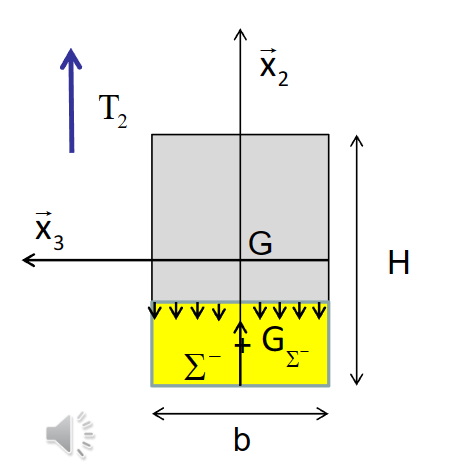
矩形情况下:
\[ \left|\begin{aligned}& b\left(x_2\right)=b \\& \mu_2\left(x_2\right)=\int_{-\frac{H}{2}}^{x_2} x_2 b d x_2=\frac{b}{2}\left(x_2^2-\frac{H^2}{4}\right) \\& J_2=\int_{-\frac{H}{2}}^{+\frac{H}{2}} x_2^2 b d x_2=\frac{b^3}{12}\end{aligned}\right. \]
此时有:
\[ \begin{aligned} \sigma_{12}^{\mathrm{T}_2} & =\frac{\mathrm{T}_2}{\mathrm{~J}_2} \frac{\mu_2\left(\mathrm{x}_2\right)}{\mathrm{b}\left(\mathrm{x}_2\right)} =\frac{6 \mathrm{~T}_2}{\mathrm{bH}}\left[\left(\frac{\mathrm{x}_2}{\mathrm{H}}\right)^2-\frac{1}{4}\right]\\ \sigma_{13}^{\mathrm{T}_2} & =0 \end{aligned} \]
数量级关系
\[ \tau \approx \frac{F}{d^2}\quad\left| \quad \tau \approx \frac{F}{\varepsilon d}\right. \]
数量级关系总结:
\[ \begin{array}{|lll|}\hline \text { Effort normal 轴力 } & \mathrm{N} & \sigma_{11} \approx \frac{F}{A} \\\hline \text { Effort tranchant 剪力 } & \mathrm{T} & \tau_{\max } \approx \frac{F}{A} \\\hline \text { Moment torsion 扭矩 } & \mathrm{M}_{\mathrm{t}} & \tau_{\max } \approx \frac{F}{A} \frac{L}{d} \\\hline \text { Moment fléchissant 弯矩 } & \mathrm{M}_{\mathrm{f}} & \sigma_{11 \max } \approx \frac{F}{A} \frac{L}{d} \\\hline\end{array} \]
应力的约束
韧性材料(Matériau ductile)约束 Contrainte de Von Mises
\[ \sigma_{\mathrm{VM}}=\sqrt{\frac{3}{2} \mathrm{~S}_{\mathrm{ij}} \mathrm{S}_{\mathrm{ij}}}=\sqrt{\underbrace{\sigma_{11}^2}_{\sigma_{\mathrm{n}}^2}+3(\underbrace{\sigma_{12}^2+\sigma_{13}^2}_{\tau^2})}< \sigma_e \]
脆性材料(Matériau fragile)约束 Critère de Rankine
\[ \sigma_{\mathrm{I}}=\frac{1}{2}\left(\sigma_{11}+\sqrt{\sigma_{11}^2+4 \tau^2}\right)<\sigma_{rt} \quad \sigma_{\mathrm{II}}=0 \]




