RDM Chapitre 1 结构力学模型 Modѐlisation des structures en efforts
RDM Chapitre 1 结构力学模型 Modѐlisation des structures en efforts
力螺旋 Torseur
速度场 Champ des vitesse
\[ [V(A)]=\left| \begin{aligned}& \vec{\Omega}\text { (角速度) } \\& \vec{V}(A)\end{aligned}\right. \]
位移向量分配 Le Torseur distributeur des déplacements
\[ [U(A)]=\left|\begin{aligned}&{\vec{w}}(\text { vecteur rotation }) \\&{\vec{u}(A)}\end{aligned}\right. \]
力螺旋
\[ \begin{aligned} \vec{M}(B) & =\vec{M}(A)+\vec{R} \wedge \overrightarrow{A B} \\ [T(A)] & =\left|\begin{array}{l} \vec{R} \\ \vec{M}(A) \end{array}\right. \end{aligned} \]
力螺旋的变换
叉乘
\[ [T(A)] \otimes[U(A)]=\left|\begin{array}{c}\vec{R} \\\vec{M}(A)\end{array}\otimes\right| \begin{gathered}\vec{\omega} \\\vec{u}(A)\end{gathered}=\vec{R} \cdot \vec{u}(A)+\vec{\omega} \cdot \vec{M}(A) \]
微分
\[ \frac{d[\mathrm{~T}]}{\mathrm{ds}}(\mathrm{P})=\lim _{\mathrm{P}_1 \rightarrow \mathrm{P}} \frac{\left[\mathrm{T}_1\right]-[\mathrm{T}]}{\mathrm{ds}} \triangleq \left| \begin{aligned}& \frac{\mathrm{d} \overrightarrow{\mathrm{R}}}{\mathrm{ds}} \\& \frac{\mathrm{d} \overrightarrow{\mathrm{M}}}{\mathrm{ds}}+\overrightarrow{\mathrm{x}}_1 \wedge \overrightarrow{\mathrm{R}}\end{aligned}\right. \]
\[ \frac{\mathrm{d}[\mathrm{U}]}{\mathrm{ds}}=\lim _{\mathrm{P}_1 \rightarrow \mathrm{P}} \frac{\left[\mathrm{U}_1\right]-[\mathrm{U}]}{\mathrm{ds}} \triangleq\left|\begin{aligned}&\frac{\mathrm{d} \vec{\omega}}{\mathrm{ds}} \\&\frac{\mathrm{d} \overrightarrow{\mathrm{u}}}{\mathrm{ds}}+\overrightarrow{\mathrm{x}}_1 \wedge \vec{\omega}\end{aligned}\right. \]
梁模型 Theorème des poutres 和结构力学假设
- 梁 = 中心纤维 + 正截面
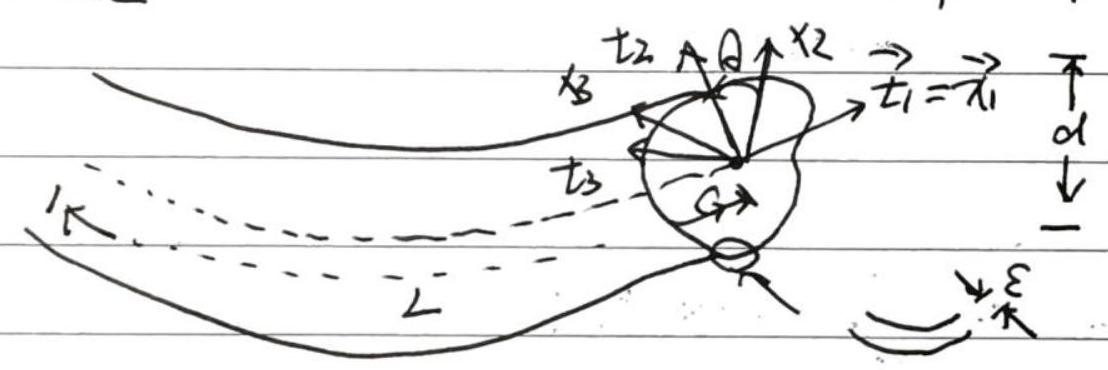
梁模型
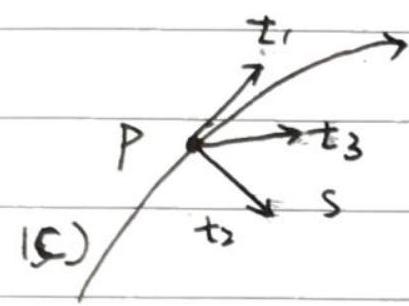
中心纤维 la fibre moyenne
- 曲线坐标系 \(\left(p, \overrightarrow{t_{1}}, \overrightarrow{t_{2}}, \overrightarrow{t_{3}}\right)\)
- \(\vec{t}_{1}\)指向曲线 \((C)\) 在 \(P\) 的切线方向
- \(\vec{t}_{2}=R(S) \frac{d \overrightarrow{t_{1}}}{d s}\),其中,\(R(S)\)代表S点的曲率半径
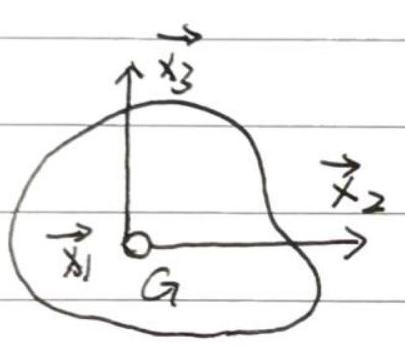
正截面 section droite
- \(G\) : 重心 centre de gravité
- \((G, \overrightarrow{x_{1}}, \overrightarrow{x_{2}} ,\overrightarrow{x_{3}})\) : 主惯性系 repѐre principale d’inertie
- \(I, I_{2}, I_{3}\) = 主惯量 Inertes principales [
假设
1. 正截面中的位移可近似为重心的位移
\[ [\mathrm{U}(\mathrm{s})]=\left|\begin{array}{l} \vec{\omega}(\mathrm{s}) \\ \overrightarrow{\mathrm{u}}(\mathrm{s}) \end{array}=\left[\mathrm{U}\left(\mathrm{G}_{\Sigma}\right)\right]=\right| \begin{aligned} & \vec{\omega}(\Sigma) \\ & \overrightarrow{\mathrm{u}}\left(\mathrm{G}_{\Sigma}\right) \end{aligned} \]
2.欧拉-伯努利假设 Hyporhèse d'Euler - Bernoulli
正截面(正交于中心纤维的面)中的位移可以忽略
\[ \left\{\begin{array}{l}\vec{x}_{2} \cdot\left(\frac{d \vec{u}}{d s}+\vec{x}_{1} \wedge \vec{w}\right)=0 \\\vec{x}_{3} \cdot\left(\frac{d \vec{u}}{d s}+\vec{x}_{1} \wedge \vec{w}\right)=0\end{array}\right. \]
3.假设干扰忽略不计
约束 liaison
约束完全与理论力学一致,重要的是未知数数量
光滑圆柱铰链 pivot articulation
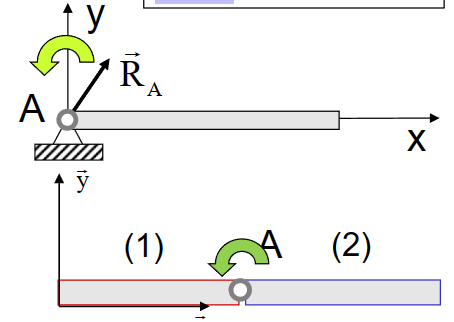
- 2D: 两个未知数
- \(\mathrm{R}_{\mathrm{Ax}}, \mathrm{R}_{\mathrm{Ay}}\)
- 3D: 五个未知数
- \(\mathrm{R}_{\mathrm{Ax}}, \mathrm{R}_{\mathrm{Ay}}, \mathrm{R}_{\mathrm{Az}}, \mathrm{M}_{\mathrm{Ax}}, \mathrm{M}_{\mathrm{Ay}}\)
点支撑 appui simple ponctuel/ supposé bilatéral
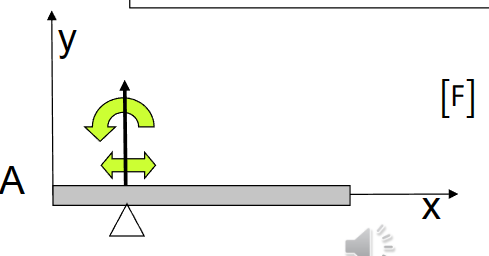
- 2D,3D:一个未知数
- \(\mathrm{R}_{\mathrm{Ax}}=\mathrm{R}_{\mathrm{Az}}=\mathrm{M}_{\mathrm{Ax}}=\mathrm{M}_{\mathrm{Ay}}=\mathrm{M}_{\mathrm{Az}}=0\)
- 未知:\(\mathrm{R}_{\mathrm{Ay}}\)
光滑球形铰链 rotule 3D
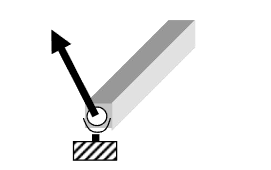
- 3D:三个未知数
- \(\mathrm{M}_{\mathrm{Ax}}=\mathrm{M}_{\mathrm{Ay}}=\mathrm{M}_{\mathrm{Az}}=0\)
固定支撑 encastrement/ liaison rigide

- 2D:三个未知数
- \(\mathrm{R}_{\mathrm{Ax}}, \mathrm{R}_{\mathrm{Ay}}, \mathrm{M}_{\mathrm{Az}}\)
- 3D:六个未知数
- \(\mathrm{R}_{\mathrm{Ax}}, \mathrm{R}_{\mathrm{Ay}}, \mathrm{R}_{\mathrm{Az}}, \mathrm{M}_{\mathrm{Ax}}, \mathrm{M}_{\mathrm{Ay}}, \mathrm{M}_{\mathrm{Az}}\)
受力分析
外力 efforts extérieur
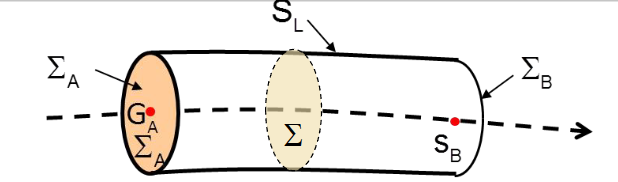
面积力 densité surfacique d’effort
- 施加在\(\sum_A\)上的面积力\(\vec T_{SA}\)
\[ \left[F_A\right]=\left| \begin{aligned}& \vec{R}_A=\int_{\Sigma_A} \vec{T}_{S A}(P) d S \\& \vec{M}_A=\int_{\Sigma_A} \overrightarrow{G_A P} \wedge \vec{T}_{S A}(P) d S\end{aligned}\right. \]
- 施加在侧面\(S_L\)上的力
\[ \left[\mathrm{f}_{\mathrm{LS}}(\mathrm{s})\right]=\left| \begin{aligned}& \overrightarrow{\mathrm{f}}(\mathrm{s})=\oint_{\delta \Sigma} \overrightarrow{\mathrm{T}}_{\mathrm{SL}} \\& \overrightarrow{\mathrm{m}}(\mathrm{s})=\oint_{\delta \Sigma} \overrightarrow{\mathrm{G} P} \wedge \overrightarrow{\mathrm{T}}_{\mathrm{SL}}\end{aligned}\right. \]
体积力 densité volumique d’effort
- 体积力 \(\vec f_v\)
\[ \left[\mathrm{f}_{\mathrm{LV}}(\mathrm{s})\right]=\left| \begin{aligned} & \overrightarrow{\mathrm{f}}(\mathrm{s})=\int_{\Sigma} \overrightarrow{\mathrm{f}}_{\mathrm{V}}(\mathrm{P}) \mathrm{dS} \\ & \overrightarrow{\mathrm{m}}(\mathrm{s})=\int_{\Sigma} \overrightarrow{\mathrm{GP}} \wedge \overrightarrow{\mathrm{f}}_{\mathrm{V}}(\mathrm{P}) \mathrm{dS} \end{aligned}\right. \]
局域力 effort localisé
按照理论力学处理即可
外力平衡
外力平衡方程
对于每个结构体,有三个方程
\[ 对于结构体i:\sum_{j}[R^{j}_{\rightarrow i}]+\sum_{k}[R^{k}_{k\rightarrow i}]+\sum_{m}[F^{m}_{\rightarrow i}] = 0 \]
- \(\sum_{j}[R^{j}_{\rightarrow i}]\)代表约束对结构体的作用
- \(\sum_{k}[R^{k}_{k\rightarrow i}]\)代表其他结构体对结构体的作用
- \(\sum_{m}[F^{m}_{\rightarrow i}]\)代表结构体所受外力
方程与未知数数量
- \(NE=NI\)
静定问题
Problème isostatique - \(NE<NI\)
超静定问题
Problème hyperstatique - \(NE>NI\)
静不定问题
Configuration hors équilibre
内力
对于某一点s,将其切断以研究内力

内力
\[ [\mathrm{T}] \triangleq\left[\mathrm{T}_{1 \rightarrow 2}\right]=-\left[\mathrm{T}_{2 \rightarrow 1}\right]=\left| \begin{gathered}\overrightarrow{\mathrm{R}}\left(\mathrm{s}_0\right) \\\overrightarrow{\mathrm{M}}_{\mathrm{G}}\left(\mathrm{s}_0\right)\end{gathered}\right. \]
内力平衡
\[ \begin{aligned}& {[\mathrm{T}]=\sum\left[\mathrm{F}_{\rightarrow \text { amont }}\right]} \\& {[\mathrm{T}]=-\sum\left[\mathrm{F}_{\rightarrow \text { aval }}\right]}\end{aligned} \]
内力分解
- 轴力 Effort normal \(\mathrm{N}=\overrightarrow{\mathrm{x}}_1 \cdot \overrightarrow{\mathrm{R}}\)
- 剪力 Effort tranchant \(\overrightarrow{\mathrm{T}}=\overrightarrow{\mathrm{R}}-\mathrm{N} \overrightarrow{\mathrm{x}}_1=\mathrm{T}_2 \overrightarrow{\mathrm{x}}_2+\mathrm{T}_3 \overrightarrow{\mathrm{x}}_3\)
- 扭矩 Moment de torsion \(\mathrm{M}_{\mathrm{t}}=\overrightarrow{\mathrm{x}}_1 \cdot \overrightarrow{\mathrm{M}}\)
- 弯矩 Moment de flexion \(\overrightarrow{\mathrm{M}}_{\mathrm{f}}=\overrightarrow{\mathrm{M}}-\mathrm{M}_{\mathrm{t}} \overrightarrow{\mathrm{x}}_1=\mathrm{M}_{\mathrm{f} 2} \overrightarrow{\mathrm{x}}_2+\mathrm{M}_{\mathrm{f} 3} \overrightarrow{\mathrm{x}}_3\)
局域平衡方程
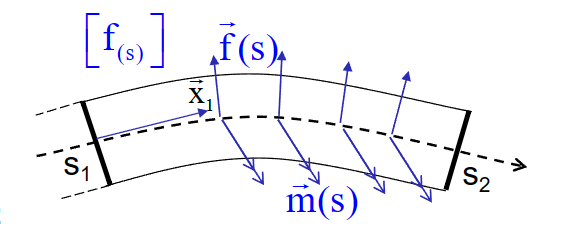
\[ -\frac{\mathrm{d}}{\mathrm{ds}}[\mathrm{T}(\mathrm{s})]+\left[\mathrm{f}_{(\mathrm{s})}\right]=[0] \]
\[ \frac{d N}{d s}=\vec{f}(s) \cdot \vec{x}_1 \quad \frac{d T_2}{d s}=\vec{f}(s) \cdot \vec{x}_2 \quad \frac{d T_3}{d s}=\vec{f}(s) \cdot \vec{x}_3 \\ \frac{d M_t}{d s}=\vec{m}(s) \cdot \vec{x}_1 \quad \frac{d M_{f 2}}{d s}-T_3=\vec{m}(s) \cdot \vec{x}_2 \quad \frac{d M_{f 3}}{d s}+T_2=\vec{m}(s) \cdot \vec{x}_3 \]




