MMC Chapitre 4 能量分析

问题的一般形式 Problémes réguliers

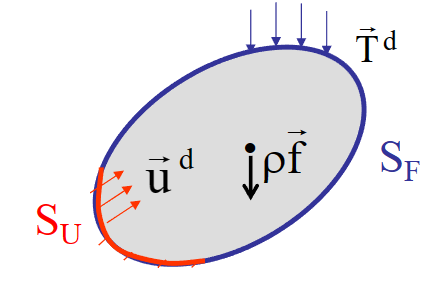
• $S_u$：已知位移的部分
• $S_F$：已知所受面积力的部分，包括面积力为零（Libre）

连续介质力学方程

$$\left\{\begin{aligned}& \sum_{\mathrm{j}=1,3} \frac{\partial \sigma_{i j}}{\partial x_j}+\rho f_i=0 \quad i=1,2,3 \\& \varepsilon_{i j}=\frac{1}{2}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right) \\& \underline{\underline{\sigma}}=\lambda \operatorname{trace}(\underline{\underline{\varepsilon}}) \underline{\underline{I}}+2 \mu \underline{\underline{\varepsilon}}\Leftrightarrow \underline{\underline{\varepsilon}} = \frac{1+v}E\underline{\underline\sigma}-\frac{v}{E}trace({\underline{\underline\sigma}})\underline{\underline I}\end{aligned}\right.$$

边界条件

$$\begin{array}{|ll|} \hline \underline{\sigma}=\underline{\mathrm{T}}^{\mathrm{d}} & \underline{\mathrm{T}}^{\mathrm{d}} \text { efforts donnés sur } \mathrm{S}_{\mathrm{F}} \\ \underline{\mathrm{u}}=\underline{\mathrm{u}}^{\mathrm{d}} & \underline{\mathrm{u}}^{\mathrm{d}} \text { déplacements imposés sur } \mathrm{S}_{\mathrm{U}}\\\hline \end{array}$$

两个解题方向

从应变信息出发

• 给出$\underline{\mathrm{\tilde u}}=\underline{\mathrm{u}}^{\mathrm{d}}$，验证是否满足要求
• 计算应力：

$$\mathrm{\tilde u}_{\mathrm{i}}(\underline{\mathrm{x}}) \underset{\varepsilon_{\mathrm{ij}}=\frac{1}{2}\left(\frac{\partial \mathrm{u}_{\mathrm{i}}}{\partial \mathrm{x}_{\mathrm{j}}}+\frac{\partial \mathrm{u}_{\mathrm{j}}}{\partial \mathrm{x}_{\mathrm{i}}}\right)}{\longrightarrow} \tilde \varepsilon_{\mathrm{ij}}(\underline{\mathrm{x}}) \underset{\underline{\underline{\sigma}}=\lambda \operatorname{trace}(\underline{\underline{\varepsilon}}) \underline{\underline{\mathrm{I}}}+2 \mu \underline{\underline{\varepsilon}}}{\longrightarrow} \tilde \sigma_{\mathrm{ij}}(\underline{\mathrm{x}})$$

• 验证是否满足平衡方程

$$\sum_{j=1,3} \frac{\partial \tilde \sigma_{i j}}{\partial x_j}+\rho f_i=0 \quad i=1,2,3$$

• 验证是否满足应力的初始条件

$$\underline{\underline{\tilde \sigma}} \underline{\underline{n}}=\underline{\mathrm{T}}^{\mathrm{d}}$$

从应力信息出发

• 给出应力场$\sigma{i j}(\vec{x})$，验证是否满足初始条件$[\hat \sigma] \mathrm{n}=\mathrm{T}^{\mathrm{d}}$和平衡方程$\sum{j=1,3} \frac{\partial \hat \sigma_{i j}}{\partial x_j}+\rho f_i=0 \quad i=1,2,3$
• 计算形变场

$$\underline{\underline{\hat \varepsilon}}=\frac{(1+v)}{\mathrm{E}} \underline{\underline{\hat \sigma}}-\frac{v}{\mathrm{E}} \operatorname{trace}(\underline{\underline{\hat \sigma}}) \underline{\underline{I}}$$

• 计算位移

$$\frac{1}{2}\left(\frac{\partial \mathrm{\hat u}_{\mathrm{i}}}{\partial \mathrm{x}_{\mathrm{j}}}+\frac{\partial \mathrm{\hat u}_{\mathrm{j}}}{\partial \mathrm{x}_{\mathrm{i}}}\right)=\hat \varepsilon_{\mathrm{ij}}$$

• 验证位移初始条件

$$\mathrm{\hat u}=\mathrm{u}^{\mathrm{d}}$$

静力学可行场和运动学可行场

Champ Cinématiquement Admissible & Champ Statiquement Admissible

CCA 和 CSA

• 当$\underline{\mathrm{u}}$满足$\underline{\mathrm{u}}=\underline{\mathrm{u}}^{\mathrm{d}} \operatorname{sur} \mathrm{S}_{\mathrm{u}}$，则成$\underline u$为CCA，记作$\tilde{\underline{u}}$
• 当$\underline{\underline{\sigma}}$满足 $\underline{\operatorname{div}}(\underline{\underline{\sigma}})+\rho \underline{f}=0$ 和 $\underline{\sigma} \underline{\underline{n}}=\mathrm{T}^{\mathrm{d}} \text { sur } \mathrm{S}_{\mathrm{F}}$，成$\underline{\underline{\sigma}}$为CSA，记作$\hat{\underline{\underline{\sigma}}}$

基本引理

$$\int_{\mathrm{V}} \underline{\hat{\underline\sigma}}: \underline{\tilde{\underline\varepsilon}}=\underbrace{\int_{\mathrm{V}} \rho \underline{\mathrm{f}} \cdot \underline{\tilde{\mathrm{u}}}+\int_{\mathrm{S}_{\mathrm{F}}} \underline{\mathrm{T}}^{\mathrm{d}} \cdot \underline{\tilde{\mathrm{u}}}}_{\mathrm{W}_{\mathrm{f}}^{\mathrm{d}}(\tilde{\mathrm{u}})}+\underbrace{\int_{\mathrm{S}_{\mathrm{U}}} \underline{\hat{\sigma}} \underline{\underline{n}} \cdot \underline{\mathrm{u}}^{\mathrm{d}}}_{\mathrm{W}_{\mathrm{u}}^{\mathrm{d}}(\hat{\sigma})}$$

• 其中，$\mathrm{W}{\mathrm{f}}^{\mathrm{d}}$和$\mathrm{W}{\mathrm{u}}^{\mathrm{d}}$分别为 $\underline{\tilde{\mathrm{u}}}$ $\underline{\tilde{\mathrm{u}}}$$\hat{\underline{\sigma}}$ 所做的功

证明过程

• $\underline{\operatorname{div}}(\underline{\hat{\underline\sigma}})+\rho \underline{f}=\underline{0}$
• 积分：$\int{\mathrm{V}} \underline{\tilde{\mathrm{u}}} \cdot(\underline{\operatorname{div}}(\underline{\hat{\underline\sigma}})+\rho \underline{f})=0 = \int{\mathrm{V}} \underline{\tilde{\mathrm{u}}} \cdot(\underline{\operatorname{div}}(\underline{\underline{\hat{\sigma}}})) +\int_{\mathrm{V}} \underline{\tilde{\mathrm{u}}} \cdot \rho \underline{f}$

• 处理第一项，应用乘法的微分公式：

  $$\int_{\mathrm{V}} \underline{\underline{\mathrm{u}}} \cdot(\underline{\operatorname{div}(\underline{\hat{\sigma}})})=\int_{\mathrm{S}}(\underline{\hat{\sigma}} \underline{\underline{n}}) \cdot \underline{\tilde{\mathrm{u}}}-\int_{\mathrm{V}} \hat{\underline{\hat{\sigma}}}: \underbrace{\operatorname{grad}(\underline{\tilde{u}})}_{\underline{\tilde{\mathrm{H}}}}$$
  • 处理第一项：
    • $\int{\mathrm{S}}(\underline{\underline{\hat{\sigma}}} \underline{\mathrm{n}}) \cdot \underline{\tilde{\mathrm{u}}}=\int{\mathrm{S}{\mathrm{F}}}(\underline{\underline{\hat{\sigma}}} \underline{\mathrm{n}}) \cdot \underline{\tilde{\mathrm{u}}}+\int{\mathrm{S}_{\mathrm{U}}}(\underline{\underline{\hat{\sigma}}} \underline{\mathrm{n}}) \cdot \underline{\tilde{\mathrm{u}}}$
    • $\int{\mathrm{S}}(\underline{\underline{\hat{\sigma}}} \underline{\mathrm{n}}) \cdot \underline{\tilde{\mathrm{u}}}=\int{\mathrm{S}{\mathrm{F}}} \mathrm{T}^{\mathrm{d}} \cdot \underline{\tilde{\mathrm{u}}}+\int{\mathrm{S}_{\mathrm{U}}}(\underline{\underline{\hat{\sigma}}} \underline{\underline{n}}) \cdot \mathrm{u}^{\mathrm{d}}$
  • 处理第二项：
    • $\underline{\underline{\hat{\sigma}}}: \underline{\underline{\underline{\mathrm{H}}}}=\underline{\underline{\hat{\sigma}}}: \frac{1}{2}\left(\underline{\underline{\tilde{\mathrm{H}}}}+\underline{\underline{\tilde{H}}}^{\mathrm{t}}\right)=\underline{\underline{\underline{\sigma}}}: \underline{\underline{\tilde{\varepsilon}}}$
• 得到结果

势能定理

也有译作能量势定理的

由CCA计算的应变能

$$\mathrm{W}(\tilde{\mathrm{u}})=\frac{1}{2} \int_{\mathrm{D}} \tilde{\sigma}: \tilde{\varepsilon} \ , \ d \tilde{\varepsilon}_{\mathrm{ij}}=\frac{1}{2}\left(\frac{\partial \mathrm{u}_{\mathrm{i}}}{\partial \mathrm{x}_{\mathrm{j}}}+\frac{\partial \mathrm{u}_{\mathrm{j}}}{\partial \mathrm{x}_{\mathrm{i}}}\right), \underline{\underline{\tilde{\sigma}}}=\lambda \operatorname{trace}(\underline{\underline{\tilde{\varepsilon}}}) \underline{\underline{\mathrm{I}}}+2 \mu \underline{\underline{\tilde{\varepsilon}}}$$

外力做功

$$\mathrm{W}_{\mathrm{f}}^{\mathrm{d}}(\underline{\tilde{\mathrm{u}}})=\int_{\mathrm{D}} \rho \underline{\mathrm{f}} \cdot \underline{\tilde{\mathrm{u}}}+\int_{\mathrm{S}_{\mathrm{F}}} \underline{\mathrm{T}}^{\mathrm{d}} \cdot \underline{\tilde{\mathrm{u}}}$$

势能

$$\mathcal{U}(\underline{\tilde{\mathrm{u}}})=\mathrm{W}(\underline{\tilde{\mathrm{u}}})-\mathrm{W}_{\mathrm{f}}^{\mathrm{d}}(\underline{\tilde{\mathrm{u}}})$$

势能定理

$$\mathcal{U}(\underline{\mathrm{u}}) \leq \mathcal{U}(\underline{\tilde{\mathrm{u}}})$$

补充能量定理

由CSA计算的应变能

$$\mathrm{W}\left(\hat{\sigma}_{\mathrm{ij}}\right)=\frac{1}{2} \int_{\mathrm{D}} \hat{\sigma}: \hat{\varepsilon} \quad \underline{\hat{\underline\varepsilon}}=\frac{(1+v)}{\mathrm{E}} \hat{\underline{\underline\sigma}}-\frac{v}{\mathrm{E}} \operatorname{trace}(\underline{\underline{\sigma}}) \underline{\underline{I}}$$

位移做功

$$\mathrm{W}_{\mathrm{u}}^{\mathrm{d}}(\underline{\underline{\hat{\sigma}}})=\int_{\mathrm{S}_{\mathrm{u}}} \underline{\hat{\underline\sigma}} \underline{n} \cdot \mathrm{u}^{\mathrm{d}}$$

补充能量

$$H(\underline{\hat{\sigma}})=\mathrm{W}_{\mathrm{u}}^{\mathrm{d}}(\underline{\hat{\sigma}})-\mathrm{W}(\underline{\hat{\sigma}})$$

补充能量定理

$$H(\underline{\underline{\sigma}}) \geq H(\underline{\underline{\underline{\sigma}}})$$

辅助原理 Theoremes annexes

Théorème de comparaison

$$H(\underline{\underline{\hat{\sigma}}}) \leq\{H(\underline{\underline{\sigma}})=\mathrm{U}(\underline{\mathrm{u}})\} \leq \mathrm{U}(\underline{\tilde{\mathrm{u}}})$$ $$H(\underline{\underline{\sigma}})+\mathrm{U}(\underline{\mathrm{u}})=\mathrm{W}_{\mathrm{u}}^{\mathrm{d}}(\underline{\underline{\sigma}})-\mathrm{W}_{\mathrm{F}}^{\mathrm{d}}(\underline{\mathrm{u}})$$ $$H(\underline{\underline{\sigma}})=\mathrm{U}(\underline{\mathrm{u}})=\frac{1}{2}\left\{\mathrm{~W}_{\mathrm{u}}^{\mathrm{d}}(\underline{\underline{\sigma}})-\mathrm{W}_{\mathrm{F}}^{\mathrm{d}}(\underline{\mathrm{u}})\right\}$$

Théorème du travail

$$H(\underline{\underline{\sigma}})-\mathrm{U}(\underline{\mathrm{u}})=0 \rightarrow \mathrm{W}=\frac{1}{2}\left\{\mathrm{~W}_{\mathrm{u}}^{\mathrm{d}}(\underline{\underline{\sigma}})+\mathrm{W}_{\mathrm{F}}^{\mathrm{d}}(\underline{\mathrm{u}})\right\}$$

示例

平面变形

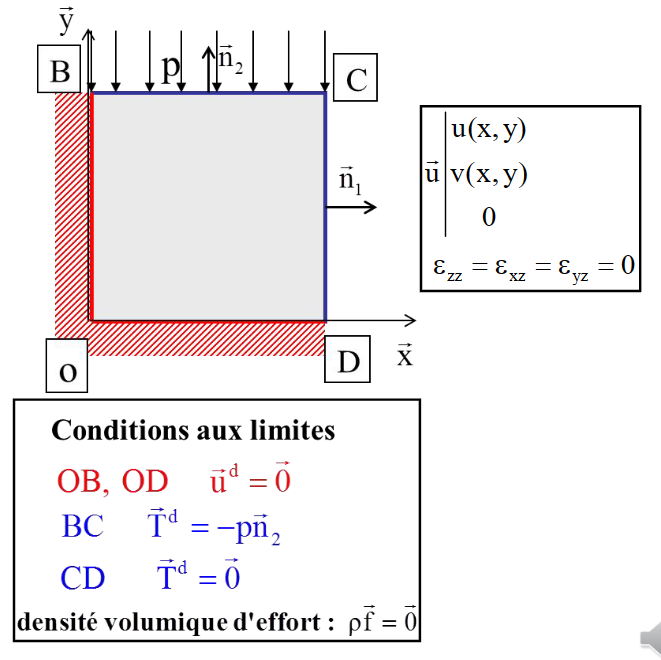
OB，OD已知位移为0，提供CCA信息

BC，CD已知受力，提供CSA信息

• CCA：
  • $\tilde{\overrightarrow{\mathrm{u}}}=\overrightarrow{0}$
  • $\mathrm{U}(\underline{\tilde{\mathrm{u}}})=\mathrm{W}(\underline{\tilde{\mathrm{u}}})-\int{\mathrm{S}{\mathrm{BC}}}-\mathrm{p}_2 \cdot \underline{\tilde{\mathrm{u}}}$
• CSA:
  • $\begin{aligned}& \operatorname{div}(\underline{\underline{\sigma}})=\underline{0}\quad &\text{sur }(\mathrm{D}) \& \underline{\underline{\hat{\sigma}}} \underline{\mathrm{n}}_1=\underline{0} \quad &\text {sur CD } \& \underline{\underline{\hat{\sigma}}} \underline{\mathrm{n}}_2=-\mathrm{p}_2 \quad &\text {sur } \mathrm{BC}\end{aligned}$
  • $\mathrm{W}_{\mathrm{u}}^{\mathrm{d}}(\underline{\underline{\hat{\sigma}}})=0$
  • $H(\underline{\underline{\underline{\sigma}}})=-\mathrm{W}(\underline{\underline{\hat{\sigma}}})$
• $H(\underline{\underline{\sigma}})=\mathrm{U}(\underline{\mathrm{u}})=\frac{1}{2}\left{\mathrm{~W}{\mathrm{u}}^{\mathrm{d}}(\underline{\underline{\sigma}})-\mathrm{W}{\mathrm{F}}^{\mathrm{d}}(\underline{\mathrm{u}})\right}$
  • $H(\underline{\underline{\sigma}})=\mathrm{U}(\underline{\mathrm{u}})=0-\frac{1}{2} \int_{\mathrm{BC}}-\mathrm{p}_2 \cdot \underline{\mathrm{u}}$
• $H(\underline{\underline{\hat{\sigma}}}) \leq H(\underline{\underline{\sigma}})=\mathrm{U}(\underline{\mathrm{u}}) \leq \mathrm{U}(\underline{\underline{\mathrm{u}}})$
  • $H(\underline{\underline{\hat{\sigma}}}) \leq \frac{\mathrm{p}}{2} \int_{\mathrm{BC}} \overrightarrow{\mathrm{n}}_2 \cdot \overrightarrow{\mathrm{u}} \leq \mathrm{U}(\underline{\tilde{\mathrm{u}}})$

近似求解

• 设：

$$\begin{aligned}& u=a_0+a_1 x+a_2 y+a_3 x y \\& v=b_0+b_1 x+b_2 y+b_3 x y\end{aligned}$$

计算CCA

• 根据CCA：

$$\text { sur }OD \ \mathrm{y}=0 \left|\begin{aligned} & \mathrm{u}(\mathrm{x}, 0)=0 \Rightarrow \mathrm{a}_0+\mathrm{a}_1 \mathrm{x}=0 \quad \forall \mathrm{x} \\ & \Rightarrow \mathrm{a}_0=\mathrm{a}_1=0 \\ & \mathrm{v}(\mathrm{x}, 0)=0 \Rightarrow \mathrm{b}_0+\mathrm{b}_1 \mathrm{x}=0 \quad \forall \mathrm{x} \\ & \Rightarrow \mathrm{b}_0=\mathrm{b}_1=0 \end{aligned}\right.$$ $$\operatorname{sur} O B \ x=0 \left|\begin{aligned}& u(0, y)=0 \Rightarrow a_2 y=0 \Rightarrow a_2=0 \\& v(0, y)=0 \Rightarrow b_2 y=0 \Rightarrow b_2=0\end{aligned}\right.$$

• 得到：

$$\begin{array}{ll}\widetilde{u}(x, y)=a_3 x y & \widetilde{u}(C)=a_3 L^2=U \\\widetilde{v}(x, y)=b_3 x y & \widetilde{v}(C)=b_3 L^2=V \\C C A: & \widetilde{u}(x, y)=U \frac{x y}{L^2} \quad \widetilde{v}(x, y)=V \frac{x y}{L^2}\end{array}$$

计算应变和应力

• 求导求出应变

$$\underline{\underline{\tilde{\varepsilon}}}=\frac{1}{L^2}\left[\begin{array}{ccc}\mathrm{Uy} & (\mathrm{Ux}+\mathrm{Vy}) / 2 & 0 \\(\mathrm{Ux}+\mathrm{Vy}) / 2 & \mathrm{Vx} & 0 \\0 & 0 & 0\end{array}\right]$$

• 应用胡克定律求出应力

$$\tilde{\sigma}=\frac{1}{L^2}\left[\begin{array}{ccc} (\lambda+2 \mu) U y+\lambda V x & \mu(U x+V y) & 0 \\ \mu(U x+V y) & (\lambda+2 \mu) V x+\lambda U y & 0 \\ 0 & 0 & 2 \mu(U x+V y) \end{array}\right]$$

计算形变能

$$\mathrm{W}(\underline{\tilde{u}})=\frac{1}{2} \int_{\mathrm{V}}(\underline{\underline{\sigma}}: \underline{\underline{\tilde{\varepsilon}}}) \mathrm{dV}$$ $$\begin{array}{l}\mathrm{W}(\underline{\tilde{\mathrm{u}}})=\frac{1}{2 \mathrm{~L}^4} \int_{\mathrm{D}} \mathrm{dxdydz}\left\{\begin{array}{l}\mathrm{U}^2\left[(\lambda+3 \mu) \mathrm{y}^2+\mu \mathrm{x}^2\right] \\+\mathrm{V}^2\left[(\lambda+2 \mu) \mathrm{x}^2+\mu \mathrm{y}^2\right] \\+2 \mathrm{UV}(\lambda+\mu) \mathrm{xy}\end{array}\right\} \\\mathrm{W}(\underline{\tilde{\mathrm{u}}})=\frac{\mathrm{e}}{2}\left\{\frac{\lambda+3 \mu}{3} \mathrm{U}^2+\frac{\lambda+3 \mu}{3} \mathrm{~V}^2+2 \mathrm{UV} \frac{\lambda+\mu}{4}\right\}\end{array}$$

计算力所做的功

$$\mathrm{W}_{\mathrm{F}}^{\mathrm{d}}=\int_{\mathrm{BC}} \mathrm{T}_{\mathrm{i}}^{\mathrm{d}} \tilde{\mathrm{u}}_{\mathrm{i}}=\int_{\mathrm{BC}}-\mathrm{p} \cdot \tilde{\mathrm{v}}(\mathrm{x}, \mathrm{L}) \mathrm{dxdz}=-\frac{\mathrm{pV}}{\mathrm{L}} \int_{\mathrm{BC}} \mathrm{xdxdz}=-\frac{\mathrm{e}}{2} \mathrm{pVL}$$

给出势能

$$\mathcal{U}(\underline{\tilde{\mathrm{u}}})=\mathrm{W}(\underline{\tilde{\mathrm{u}}})-\mathrm{W}_{\mathrm{F}}^{\mathrm{d}}(\underline{\tilde{\mathrm{u}}}) = \frac{\mathrm{e}}{2}\left\{\frac{\lambda+3 \mu}{3} \mathrm{U}^2+\frac{\lambda+3 \mu}{3} \mathrm{~V}^2+2 \mathrm{UV} \frac{\lambda+\mu}{4}+\frac{\mathrm{pL}}{2} \mathrm{~V}\right\}$$

※估计势能最小值

• 在势能最小值时，应有导数为0

$$\frac{\partial \mathrm{U}}{\partial \mathrm{U}}=0 \ \frac{\partial \mathrm{U}}{\partial \mathrm{V}}=0\Leftrightarrow \left| \begin{aligned} & \frac{\lambda+3 \mu}{3} \mathrm{U}+\frac{\lambda+\mu}{4} \mathrm{~V}=0 \\ & \frac{\lambda+\mu}{4} \mathrm{U}+\frac{\lambda+3 \mu}{3} \mathrm{~V}=-\frac{\mathrm{pL}}{2} \end{aligned}\right.$$

• 得到

$$\mathrm{U}=\mathrm{pL} \frac{18(\lambda+\mu)}{(\lambda+9 \mu)(7 \lambda+15 \mu)} \\ \mathrm{V}=-\mathrm{pL} \frac{24(\lambda+3 \mu)}{(\lambda+9 \mu)(7 \lambda+15 \mu)}$$

• 代入实际值

$$v=0.25 \Rightarrow \lambda=\mu=\frac{2 \mathrm{E}}{5} \Rightarrow \quad \mathrm{U}=\frac{9 \mathrm{~L}}{22 \mathrm{E}} \mathrm{p} \quad \mathrm{V}=-\frac{24 \mathrm{~L}}{22 \mathrm{E}} \mathrm{p}$$