MMC Chapitre 3 完备性方程 Loi de comportement

方程数量与未知数数量

	Inconnues
$u_i(\vec{x}, t)$	déplacements: vecteur	3 inconnues
$\varepsilon_{i j}$	déformations: tenseur symétrique	6 inconnues
$\sigma_{i j}$	contraintes: tenseur symétrique	6 inconnues
	Équations
$\varepsilon_{i j}=\frac{1}{2}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)$	déformation - déplacement	6 équations
$\sum{j=1,2.3} \frac{\partial \sigma{i j}}{\partial x_j}+\rho f_i=0$	équation d’équilibre locale	3 équations
$\sigma{i j} \leftrightarrow \varepsilon{i j}$	loi de comportement	6 équations
	Conditions aux limites
$\sigma_{i j} n_j=T_i^d$	$T_i^d$ efforts donnés sur $S_D$
$u_i=u_i^d$	$u_i^d$ déplacements imposés sur $S_D$

虎克定律 Comportement élastique linéaire

弹性刚度矩阵 Matrice de raideur élastique

将应力 $\bar{\sigma}$ 和应变 $\bar{\varepsilon}$ 表示为一维数组，其中 $\sigma{ij}$ 是应力张量的元素， $\varepsilon{ij}$ 是应变张量的元素。注意，剪切应变的表示方式是原始值的两倍。

$\bar{\sigma}=\left[\begin{array}{l}\sigma_{11} \\\sigma_{22} \\\sigma_{33} \\\sigma_{23} \\\sigma_{13} \\\sigma_{12}\end{array}\right] \quad \bar{\varepsilon}=\left[\begin{array}{c}\varepsilon_{11} \\\varepsilon_{22} \\\varepsilon_{33} \\2 \varepsilon_{23} \\2 \varepsilon_{13} \\2 \varepsilon_{12}\end{array}\right] \ \ avec \ \ \left\{\begin{aligned}&\gamma_{23}=2 \varepsilon_{23} \\ &\gamma_{13}=2 \varepsilon_{13} \\ &\gamma_{12}=2 \varepsilon_{12}\end{aligned}\right.$

表示为胡克定律的形式

$\bar{\sigma}=\underline{\underline{A}} \overline{\underline{\varepsilon}}$

其中，$\underline{\underline{A}}$ 是弹性模量矩阵。这个公式表示了应力和应变之间的线性关系。

$\underline{A}=\left[\begin{array}{cccccc}\lambda+2 \mu & \lambda & \lambda & 0 & 0 & 0 \\\lambda & \lambda+2 \mu & \lambda & 0 & 0 & 0 \\\lambda & \lambda & \lambda+2 \mu & 0 & 0 & 0 \\0 & 0 & 0 & \mu & 0 & 0 \\0 & 0 & 0 & 0 & \mu & 0 \\0 & 0 & 0 & 0 & 0 & \mu\end{array}\right]$

应力和应变张量的关系

在以上公式的基础上，得到应力和应变张量的关系

$\underline{\underline{\sigma}}=\lambda \operatorname{trace}(\underline{\underline{\varepsilon}}) \underline{\underline{I}}+2 \mu \underline{\underline{\varepsilon}} \Leftrightarrow \sigma_i=\lambda\left(\varepsilon_1+\varepsilon_2+\varepsilon_3\right)+2 \mu \varepsilon_i$

韧性矩阵 la matrice de souplesse $\underline{S}=\underline{A}^{-1}$

$\underline{S}=\frac{1}{E}\left[\begin{array}{cccccc}1 & -v & -v & 0 & 0 & 0 \\-v & 1 & -v & 0 & 0 & 0 \\-v & -v & 1 & 0 & 0 & 0 \\0 & 0 & 0 & 2(1+v) & 0 & 0 \\0 & 0 & 0 & 0 & 2(1+v) & 0 \\0 & 0 & 0 & 0 & 0 & 2(1+v)\end{array}\right]$

应变和应力张量的关系

$\underline{\underline{\varepsilon}}=\frac{(1+\nu)}{E} \underline{\underline{\sigma}}-\frac{\nu}{E} \operatorname{trace}(\underline{\underline{\sigma}}) \underline{\underline{I}}$

二维问题

$A=\frac{E}{1-v^2}\left[\begin{array}{ccc}1 & v & 0 \\v & 1 & 0 \\0 & 0 & \frac{1-v}{2}\end{array}\right], \operatorname{avec}\left\{\begin{array}{l}\sigma_{33}=0 \\\sigma_{13}=0 \\\sigma_{23}=0\end{array}\right.$ $A=\left[\begin{array}{ccc}\lambda+2 \mu & \lambda & 0 \\\lambda & \lambda+2 \mu & 0 \\0 & 0 & \mu\end{array}\right] \text {, avec }\left\{\begin{array}{l}u_3=0 \\\varepsilon_{33}=0 \\\varepsilon_{13}=0 \\\varepsilon_{23}=0\end{array}\right.$

特殊的应力和变形

球形形变的受压的情况

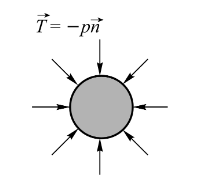
应力

$\bar{\sigma}=\left[\begin{array}{l}\sigma \\\sigma \\\sigma \\0 \\0 \\0\end{array}\right], \sigma=(3 \lambda+2 \mu) \varepsilon$

应变

$\bar{\varepsilon}=\left[\begin{array}{l}\varepsilon \\\varepsilon \\\varepsilon \\0 \\0 \\0\end{array}\right]$ $\underline{\underline{\sigma}}=\left[\begin{array}{ccc}\sigma & 0 & 0 \\0 & \sigma & 0 \\0 & 0 & \sigma\end{array}\right] \quad \underline{\underline{\varepsilon}}=\left[\begin{array}{ccc}\varepsilon & 0 & 0 \\0 & \varepsilon & 0 \\0 & 0 & \varepsilon\end{array}\right]$

可见应变与应力呈线性关系：$\sigma=(3 \lambda+2 \mu) \varepsilon$
体积相对变化：$\alpha = \frac{\Delta V}{V}=3 \varepsilon$
此时，可以定义体积压缩模量 module de compressibilité volumique:

$\sigma=K \alpha \text { avec } K=\frac{(3 \lambda+2 \mu)}{3}$

简单剪切情况

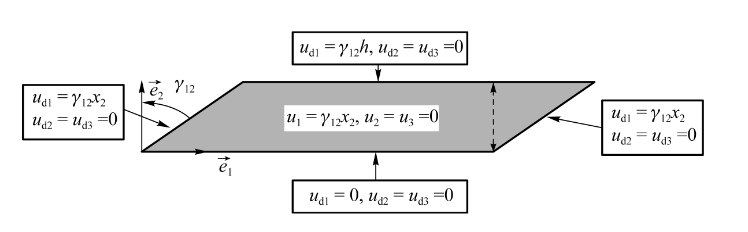
注意，这并不是一个平方的板，而是竖放的收到剪切力而变形的薄板，此外，我们讨论的情况是$\gamma_{12}$很小的情况
在$\gamma_{12}$很小的形况下，仅有横向的平移，且大小取决于角速度和坐标$x_2$，有：

$\varepsilon_{12}=\varepsilon_{21}=\frac{1}{2} \frac{\mathrm{d} u_1}{\mathrm{~d} x_2} = \frac 12 \gamma_{12},\ \underline{\underline{\varepsilon}}=\left[\begin{array}{ccc} 0 & \varepsilon_{12} & 0 \\ \varepsilon_{12} & 0 & 0 \\ 0 & 0 & 0 \end{array}\right]$

此时，根据胡可定律$\underline{\underline{\sigma}}=\lambda \operatorname{trace}(\underline{\underline{\varepsilon}}) \underline{\underline{I}}+2 \mu \underline{\underline{\varepsilon}}$，有：

$\sigma_{12}=2 \mu \varepsilon_{12}=\mu \gamma_{12}, \ \underline{\underline{\sigma}}=\left[\begin{array}{ccc} 0 & \sigma_{12} & 0 \\ \sigma_{12} & 0 & 0 \\ 0 & 0 & 0 \end{array}\right]$

此时可以定义剪切模量module de cisaillement

$\mu=G \text {. }$

简单拉伸情况

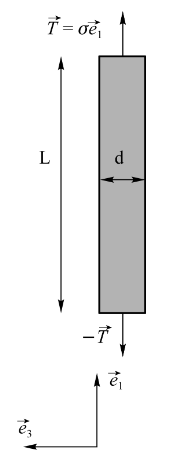
这种情况下，应力仅有$x_1$上的正应力：

$\underline{\underline{\sigma}}=\left[\begin{array}{lll}\sigma & 0 & 0 \\0 & 0 & 0 \\0 & 0 & 0\end{array}\right]$

应变则既有正应变，又有切向应变

$\underline{\underline{\varepsilon}}=\left[\begin{array}{ccc}\varepsilon_L & 0 & 0 \\0 & \varepsilon_T & 0 \\0 & 0 & \varepsilon_T\end{array}\right]$

根据胡可定律，得到

$\left\{\begin{array} { l } { \sigma = ( \lambda + 2 \mu ) \varepsilon _ { L } + 2 \lambda \varepsilon _ { T } } \\ { 0 = 2 ( \lambda + \mu ) \varepsilon _ { T } + \lambda \varepsilon _ { L } } \end{array} \Rightarrow \left\{\begin{array}{l} \sigma=\frac{\mu(3 \lambda+2 \mu)}{\lambda+\mu} \varepsilon_L \\ \varepsilon_T=-\frac{\lambda}{2(\lambda+\mu)} \varepsilon_L \end{array}\right.\right.$

根据$E$和$v$的定义：

$E=\frac{\mu(3 \lambda+2 \mu)}{\lambda+\mu}, \quad \nu=\frac{\lambda}{2(\lambda+\mu)}$

可以定义拉美系数 coefficients de Lamé

$\lambda=\frac{E \nu}{(1+\nu)(1-2 \nu)}, \quad \mu=G=\frac{E}{2(1+\nu)}$

不同弹性常数之间的关系

-	$λ$	$μ$	$E$	$ν$	$K$	$G$
$(λ, μ)$	$λ$	$μ$	$μ(3λ+2μ)/(λ+μ)$	$λ/2(λ+μ)$	$(3λ+2μ)/3$	$μ$
$(E, ν)$	$Ev/(1+ν)(1-2ν)$	$E/2(1+ν)$	$E$	$ν$	$E/3(1-2ν)$	$E/2(1+ν)$
$(K, G)$	$(3K-2G)/3$	$G$	$9KG/(3K+G)$	$(3K-2G)/2(3K+G)$	$K$	$G$

形变能量

形变能量微元

$\mathrm{w}=\frac{1}{2} \bar{\sigma}^T \bar{\varepsilon}=\frac{1}{2} \bar{\varepsilon}^T \underline{\underline{A} \bar{\varepsilon}}=\frac{1}{2} \bar{\sigma}^T \underline{\underline{S}} \bar{\sigma} \Leftrightarrow \frac{1}{2} \sum_{i, j=1,2,3} \sigma_{i j} \varepsilon_{i j}$

形变能量

$W = \iiint_{V}w\cdot dV$

稳定性和不可压性

stabilité & incompressibilité

稳定性

$E, \mu \text { et } K$取正值
$3 \lambda+2 \mu>0$
$-1 \leqslant \nu \leqslant 1 / 2 \text {. }$

不可压性

$\lambda \gg \mu \ or \ \nu \rightarrow \frac{1}{2}$

弹性限制

Von Miss 限制

$\sigma_{V M}=\sqrt{\frac{3}{2} \underline{s}: \underline{\underline{s}}}$

$\sigma_{V M} \leqslant \sigma_e$ $\sigma_e$为弹性区限制limite du domaine élastique

Tresca 限制

$|\tau|_{\max }=\frac{1}{2}\left(\sigma_1-\sigma_3\right)$ $\sigma_T=\left(\sigma_1-\sigma_3\right)=\left(s_1-s_3\right) \leqslant \sigma_e$

$\sigma_T \leqslant \sigma_e$

Rankine限制

$\overline{\bar{\sigma}}=\left[\begin{array}{lll}\sigma & 0 & 0 \\0 & 0 & 0 \\0 & 0 & 0\end{array}\right] \text { avec } \sigma_1=\sigma, \sigma_2=\sigma_3=0$

$\sigma_1 \leqslant \sigma_r$