MMC Chapitre 1 应力 contraintes

力和平衡

外力的分类

体积力 densité volumique d’effort extérieur

均匀作用在一定体积中的力，如重力等

• 单位体积内，体积力的公式一般表示为

\[ \mathrm{d} \vec{F}_v=\rho \vec{f} \mathrm{~d} V \]

• 其中：
  • \(\rho\)表示物体的密度
  • \(\vec f\)表示体积力强度
• 在体积力与质量不相关的特殊情况，体积力也会表示为：

\[ \mathrm{d} \vec{F}_v= \vec{f} \mathrm{~d} V \]

面积力 Densité surfacique d' efforts extérieurs

• 单位面积下面积力表示为：

\[ \mathrm{d} \vec{F}=\vec{T}_{\mathrm{ext}} \mathrm{d} S \]

• 其中：

  • \(\vec T\)代表面积里强度，在某些时候也会被称为张力\(contraites\)

• 根据与表面法向量的关系，可以分解为：

  • 正应力 la contrainte normale \(T_n\)

    \[ T_n=\vec{n} \cdot \vec{T}_{\mathrm{ext}} \]

  • 切应力 la contrainte tangentielle \(\vec T_t\)

  \[ \vec{T}_t=\vec{T}_{e x t}-T_n \vec{n} \]

  • 注意，在这里的定义中，正应力不是一个向量

内力

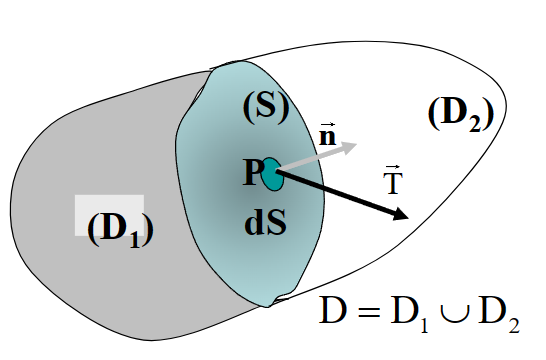
在讨论内力时，我们会将一个连续介质在某一个面“切开”研究，其中\(\vec n\)是截面的法向量，而\(\vec T\)是该面的张力

作用力-反作用定律

\[ \overrightarrow{\mathrm{T}}(\mathrm{P},-\overrightarrow{\mathrm{n}})=-\overrightarrow{\mathrm{T}}(\mathrm{P}, \overrightarrow{\mathrm{n}}) \]

柯西四面体定律

对于柯西四面体：

\[ \mathrm{T}(\mathrm{P}, \mathrm{n})=\mathrm{n}_1 \mathrm{~T}\left(\mathrm{P}, \mathrm{e}_1\right)+\mathrm{n}_2 \mathrm{~T}\left(\mathrm{P}, \mathrm{e}_2\right)+\mathrm{n}_3 \mathrm{~T}\left(\mathrm{P}, \mathrm{e}_3\right) \]

• 该公式可以很简单的由受力平衡方程得到：

\[ \sum_{\mathrm{i}=1,2,3}\left(\mathrm{~S}_{\mathrm{i}} \overrightarrow{\mathrm{T}}\left(\mathrm{P}, \overrightarrow{\mathrm{n}}_{\mathrm{i}}\right)\right)+\mathrm{S} \overrightarrow{\mathrm{T}}(\mathrm{P}, \overrightarrow{\mathrm{n}})=\overrightarrow{0} \]

应力张量 tenseur des contraintes

• 柯西四面体定律为我们提供了分解应力的另一种方法，在这种分解下，我们可以得到应力张量

\[ \underline{\mathrm{T}}(\mathrm{P}, \underline{\mathrm{n}})=\left[\begin{array}{l} \mathrm{T}_1 \\ \mathrm{~T}_2 \\ \mathrm{~T}_3 \end{array}\right]=\left[\begin{array}{l|l|l} \sigma_{11} & \sigma_{12} & \sigma_{13} \\ \sigma_{21} & \sigma_{22} & \sigma_{23} \\ \sigma_{31} & \sigma_{32} & \sigma_{33} \end{array}\right]_{\mathrm{R}}\left[\begin{array}{l} \mathrm{n}_1 \\ \mathrm{n}_2 \\ \mathrm{n}_3 \end{array}\right]_{\mathrm{R}} \]

• 表示为：

\[ \underline{\mathrm{T}}(\mathrm{P}, \underline{\mathrm{n}})=\underline{\underline{\sigma}} \underline{\mathrm{n}} \]

• \(\underline{\underline{\sigma}}\)成为R坐标系下的张力张量

从力矩平衡到应力张量的对称性

我们使用了受力平衡方程定义了张力张量，而我们将用力矩平衡方程来验证应力张量的对称性

• 力矩平衡方程：

$$
\iiint_V \vec{x} \wedge \rho(\vec{f}-\vec{a}) d v+\iint_{S_i, S} \vec{x} \wedge \vec{T} d S=\overrightarrow{0}
$$

• 接下来用张量形式证明
  • 体积力项为三阶无穷小量，是面积项的高阶无穷小，可以略去
  • 转化为张量形式
    • \(0 = \int_{s}\varepsilon_{ijk}x_j\sigma_{lk}n_{l}\)
    • 其中，\(\varepsilon\)为Levi-cicvita符号，向量叉乘就写作这个样子
  • 应用高斯公式
    • \(0 = \int_V\varepsilon_{ijk}\frac{\partial(x_j\sigma_{lk})}{\partial x_l}dV\)
    • 其中，\(\frac{\partial(x_j\sigma_{lk})}{\partial x_l}\)即为散度
  • 乘法求导法则
    • \(0 = \int_V\varepsilon_{ijk}(x_j\frac{\partial \sigma_{lk} }{\partial x_l}+\sigma_{lk}\frac{\partial x_j}{\partial x_l})dV\)
  • \(x_j\)是一阶无穷小量，消去
    • \(0 = \int_V\varepsilon_{ijk}\sigma_{lk}\frac{\partial x_j}{\partial x_l}dV = \int_V\varepsilon_{ijk}\sigma_{lk}\delta_{jl}dV = \int_V\varepsilon_{ijk}\sigma_{jk}dV\)
  • 根据\(V\)的任意性
    • \(\varepsilon_{ijk}\sigma_{jk} = 0\)
    • 由于\(j,k\)都是哑标，故可以交换
  • 由此证明其对称性
• 最终得到结论：

\[ \sigma_{\mathrm{ji}}=\sigma_{\mathrm{ij}} \]

应力张量分解

应力张量分解与应力分解基本一致

\[ \begin{aligned}& \sigma_{\mathrm{n}}=\overrightarrow{\mathrm{n}} \cdot \overrightarrow{\mathrm{T}}(\mathrm{P}, \overrightarrow{\mathrm{n}}) \\& \vec\tau=\overrightarrow{\mathrm{t}} \cdot \overrightarrow{\mathrm{T}}(\mathrm{P}, \overrightarrow{\mathrm{n}}) = \overrightarrow{\mathrm{T}}(\mathrm{P}, \overrightarrow{\mathrm{n}})-\sigma_{\mathrm{n}} \overrightarrow{\mathrm{n}}\\&\tau = |\vec \tau|\end{aligned} \]

更换坐标系

应力张量依赖坐标系

• 根据矩阵关系，我们知道：

\[ \overrightarrow{\mathrm{e}_{\mathrm{i}}} \overrightarrow{\mathrm{T}}\left(\mathrm{P}, \overrightarrow{\mathrm{e}}_{\mathrm{j}}\right)=\sigma_{\mathrm{ij}}=\underline{\mathrm{e}}^{\mathrm{t}} \underline{\underline{\sigma}} \ \underline{\mathrm{e}}_{\mathrm{j}} \]

• 同理的

\[ \overrightarrow{\mathrm{e}^{\prime}_{\mathrm{i}}} \overrightarrow{\mathrm{T}}\left(\mathrm{P}, \overrightarrow{\mathrm{e}^{\prime}}_{\mathrm{j}}\right)=\sigma^{\prime}_{\mathrm{ij}}=\underline{\mathrm{e}^{\prime}}^{\mathrm{t}} \underline{\underline{\sigma}} \ \underline{\mathrm{e}^{\prime}}_{\mathrm{j}} \]

• 因此，定义传递矩阵为新基在老基下的坐标：

\[ \underline{\underline{Q}}={ }_{\mathrm{R}}\left[\underline{\mathrm{e}}_{\mathrm{R} 1}^{\prime}\left|\underline{\mathrm{e}}_{\mathrm{R} 2}^{\prime}\right| \underline{\mathrm{e}}_{\mathrm{R} 3}^{\prime}\right] \]

• 新基下的应力张量：

\[ \underline{\underline{\sigma}}^{\prime}=\underline{Q}^t \underline{\underline{\sigma}} \ \underline{\underline{Q}} \]

从直角坐标系到柱坐标系

我们这里认为直角坐标系的z轴和柱坐标系的z轴作为\(x_1\)

• 传递方程

\[ Q = \begin{pmatrix}1 & 0 & 0\\ 0 & cos(\theta) & -sin(\theta)\\ 0 & sin(\theta) &cos(\theta)\end{pmatrix}\quad\sigma=\begin{pmatrix} 0 & -x_3 &x_2 \\ -x_3 & 0& 0\\ x_2 & 0&0 \end{pmatrix} \]

• 换基计算

\[ \sigma^{\prime} = Q^t\sigma Q =A \begin{pmatrix} 1 & 0 &0 \\ 0 & cos(\theta)& sin(\theta)\\ 0 & -sin(\theta)&cos(\theta) \end{pmatrix}\begin{pmatrix} 0 & -x_3 &x_2 \\ -x_3 & 0& 0\\ x_2 & 0&0 \end{pmatrix}\begin{pmatrix} 1 & 0 &0 \\ 0 & cos(\theta)& -sin(\theta)\\ 0 & sin(\theta)&cos(\theta) \end{pmatrix} \]

\[ =\begin{pmatrix} 0 & -x_3cos(\theta)+x_2sin(\theta) & x_3sin(\theta)+x_2cos(\theta)\\ -x_3cos(\theta)+x_2sin(\theta) & 0& 0\\ x_3sin(\theta)+x_2cos(\theta) & 0&0 \end{pmatrix} \]

\[ \left\{\begin{aligned}&x_3sin(\theta)+x_2cos(\theta) = rsin^2(\theta)+rcos^2(\theta) = r\\&-x_3cos(\theta)+x_2sin(\theta) = -rsin(\theta)cos(\theta)+rsin(\theta)cos(\theta) = 0\end{aligned}\right. \]

\[ \sigma^{\prime} = A\begin{pmatrix} 0 & 0 &r \\ 0 & 0& 0\\ r & 0&0 \end{pmatrix} \]

局部平衡方程

之前，我们使用柯西四面体上的受力平衡定义了应力张量；现在，我们在正方体上研究局部平衡

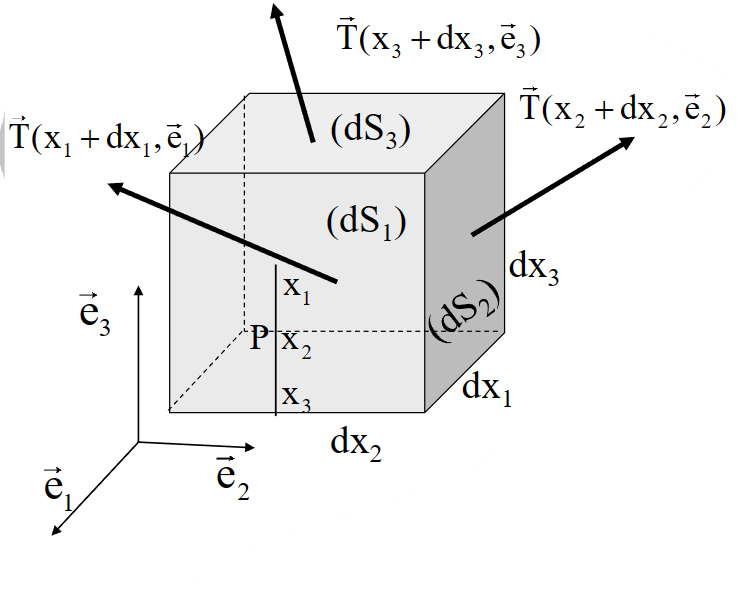
• 对于一个形状为正方体的体积微元：
• 其体积力：\(\rho(\overrightarrow{\mathrm{f}}-\overrightarrow{\mathrm{a}}) \mathrm{dV}\)
• 其面积力：\(\begin{array}{lll} &\mathrm{T}\left(\mathrm{x}_1+\mathrm{dx}_1, \mathrm{e}_1\right) \mathrm{dS}_1 ; & \mathrm{T}\left(\mathrm{x}_1,-\mathrm{e}_1\right) \mathrm{dS}_1=-\mathrm{T}\left(\mathrm{x}_1, \mathrm{e}_1\right) \cdot \mathrm{dS}_1 \\& \mathrm{~T}\left(\mathrm{x}_2+\mathrm{dx}_2, \mathrm{e}_2\right) \mathrm{dS}_2 ; & \mathrm{T}\left(\mathrm{x}_2,-\mathrm{e}_2\right) \mathrm{dS}_2=-\mathrm{T}\left(\mathrm{x}_2, \mathrm{e}_2\right) \cdot \mathrm{dS}_2 \\& \mathrm{~T}\left(\mathrm{x}_3+\mathrm{dx}_3, \mathrm{e}_3\right) \mathrm{dS}_3 ; & \mathrm{T}\left(\mathrm{x}_3,-\mathrm{e}_3\right) \mathrm{dS}_3=-\mathrm{T}\left(\mathrm{x}_3, \mathrm{e}_3\right) \cdot \mathrm{dS}_3 \end{array}\)
• 有平衡方程：

\[ \sum\left\{\overrightarrow{\mathrm{T}}\left(\mathrm{x}_{\mathrm{j}}+\mathrm{dx}_{\mathrm{j}}, \overrightarrow{\mathrm{e}}_{\mathrm{j}}\right)-\overrightarrow{\mathrm{T}}\left(\mathrm{x}_{\mathrm{j}}, \overrightarrow{\mathrm{e}}_{\mathrm{j}}\right) \cdot\right\} \mathrm{d} \mathrm{S}_{\mathrm{j}}+\rho(\overrightarrow{\mathrm{f}}-\overrightarrow{\mathrm{a}}) \mathrm{dV}=\overrightarrow{0} \]

• 当体积微元足够小：

  \[ \sum_{\mathrm{j}=1,3}\left\{\frac{\partial \overrightarrow{\mathrm{T}}\left(\mathrm{P}, \overrightarrow{\mathrm{e}}_{\mathrm{j}}\right)}{\partial \mathrm{x}_{\mathrm{j}}} \cdot\right\}+\rho(\overrightarrow{\mathrm{f}}-\overrightarrow{\mathrm{a}})=\overrightarrow{0} \]

• 得到局部平衡方程 Equations d’équilibre local

\[ \operatorname{div}(\underline{\underline{\sigma}})+\rho(\underline{\mathrm{f}}- \underline{\mathrm{a}})=\underline{0} \quad \operatorname{div}(\underline{\sigma}) \stackrel{\operatorname{def}}{=}\left|\begin{array}{l}\sum_{\mathrm{j}=1,3} \frac{\partial \sigma_{1 \mathrm{j}}}{\partial \mathrm{x}_{\mathrm{j}}} \\\sum_{\mathrm{j}=1,3} \frac{\partial \sigma_{2 \mathrm{j}}}{\partial \mathrm{x}_{\mathrm{j}}} \\\sum_{\mathrm{j}=1,3} \frac{\partial \sigma_{3 \mathrm{j}}}{\partial \mathrm{x}_{\mathrm{j}}}\end{array}\right. \]

不变量分析和正交基

同一个矩阵在不同基下为相似矩阵，这些矩阵具有若干不变量，这一部分的知识待未来代数3，4的内容被整理后给出补充

• 在这一章中，我们考虑一个满足\(\sigma_1>\sigma_2>\sigma_3\)的正交基，使得：

\[ \underline{\underline{\sigma}}_{\mathrm{p}}=\left[\begin{array}{ccc}\sigma_1 & 0 & 0 \\0 & \sigma_{2 p} & 0 \\0 & 0 & \sigma_3\end{array}\right] \]

• 换言之，我们要实现应力张量矩阵的对角化
• 对角化方式与分析中的方法一致，再次不再赘述，可参考TD2的第二题的第10小问

应力张量分解

• 并不困难，按照公式分解即可

\[ \underline{\underline{\sigma}}=\underbrace{\frac{1}{3} \operatorname{trace}(\underline{\underline{\sigma}}) \underline{\underline{I}}}_{\text {partie sphérique }}+\underbrace{\left\{\underline{\underline{\sigma}}-\frac{1}{3} \operatorname{trace}(\underline{\underline{\sigma})}) \underline{\underline{I}}\right\}}_{\begin{array}{c} \text { partie déviatorique } \\ \text { ou déviateur } \end{array}} \]

• 偏离（后半）部分被记作：\(\underline{\underline{s}}\)

\[ \operatorname{trace}(\underline{\underline{\sigma}})=\sigma_{11}+\sigma_{22}+\sigma_{33}=\sigma_{\mathrm{kk}} \]

\[ \underline{\sigma}=\underbrace{\frac{\mathbf{1}}{\mathbf{3}}\left[\begin{array}{ccc} \sigma_{\mathrm{kk}} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \sigma_{\mathrm{kk}} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \sigma_{\mathrm{kk}} \end{array}\right]}_{\text {partie sphérique }}++\underbrace{\left[\begin{array}{ccc} \sigma_{11}-\frac{1}{3} \sigma_{\mathrm{kk}} & \sigma_{12} & \sigma_{13} \\ & \sigma_{22}-\frac{1}{3} \sigma_{\mathrm{kk}} & \sigma_{23} \\ \text { sym } && \sigma_{33}-\frac{1}{3} \sigma_{\mathrm{kk}} \end{array}\right]}_{\text {déviateur de } \underline{\underline{\sigma}} \text { notés }} \]