TD 6：爱因斯坦光电效应，双能级模型

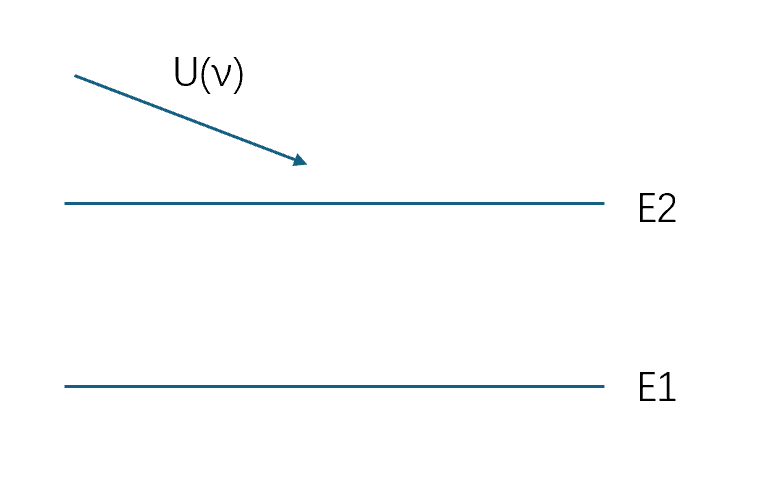
  • $h\nu_0 = E_2-E_1$

基础知识

爱因斯坦知道的信息：

  • 赫兹发现了光电效应
  • 波尔提出了原子的基本模型-行星模型，能级
  • 玻尔兹曼：$N_2/N_1 = exp(-(E_2-E_1)/kt) = exp(-h\nu/kt)$
  • 普朗克提出了量子假说：$u(\nu) = \frac{8\pi h \nu^3_0}{c^3}\frac{1}{e^{h\nu /kt}-1}$

从1到2的电子[单位时间]：

  • 受激吸收：$N1 U(\nu_0)B{12}$
  • 吸收系数：$B_{12}$

从2到1的电子

  • 自发辐射：$N2A{21}$
  • 辐射系数：$A_{21}$

电子数守恒：

带入玻尔兹曼方程

发现跟普朗克结论不一致

带回去发现：$u(\nu) = \frac AB\frac{1}{N_1/N_2-1}$

得到[稳态条件下电子平衡]：

得到受激辐射：$N2u(\nu)B{12}$

  • 受激辐射的存在
  • 受激辐射的吸收率等于吸收系数：$B{21} = B{12}$
  • $\frac AB = \frac{8\pi h \nu^3}{c^3} = \frac{8\pi h}{\lambda^3}$

其他补充：

  • $uB = W{21},\quad uB = W{12}$
  • $A = 1/\tau_{sp}$

其他其他补充：

  • 能级可能有一定宽度，只有当宽谱光覆盖了能级的宽度，$N2B = W{21},\quad N1B = W{12}$这种形式才是合理的。
  • 如果入射光是准单色光或者不能覆盖全部的宽度，则需要再加上辐射的线型函数。对于准单色光，我们称其线形函数为$g = 1/\nu_{at}$
  • $uBg = W{21},\quad uBg = W{12}$

1. 给出N1和N2的变化率

2. 估算 $N_1/N_2$和 $\delta N/N_0$，证明介质是吸收态

  • 在稳态时，有 $\frac{dN_2}{dt}=-\frac{dN_1}{dt}$
  • $AN_2+WN_2-WN_1 = 0$
  • 达到稳态后，低能级的电子数多于高能级的电子数【激光实现的关键在于实现电子数的反转】【对于二能级系统，电子数的反转是不可能的】

要验证吸收态，需判断u随位移的变化

  • 在这个过程中，$\Delta N = WN_2-WN_1$，因为入射光是有方向的，而自由辐射是无向的，不算在其中
  • $\Delta N <0$, 所以是吸收态
  • 吸收系数$\alpha = \Delta NBgh\nu\frac nc$

3. 入射能量极大时的情况

4. 氦氖激光器的$633nm$波长的光

横截面为$1mm^2$，相关长度$20cm$[相干时间$\Delta$$t = \frac {\Delta l}c$ = $2/3\times10^{-9}$]，、$\Delta \nu_{at} = 250GHz$

  • 有相干时间于线宽的关系:
  • 因此g要保留

考虑光学特性

  • $u = 0 \Rightarrow \alpha_0 = -N_0Bgh\nu\frac nc$
  • $\alpha = \alpha_0/2 \Rightarrow \Delta N = -N_0/2 \Rightarrow 1+2ug\frac BA = 2\ u = …., \quad P = usc = 2.47w$

5. 强脉冲穿过介质可以抑制展宽

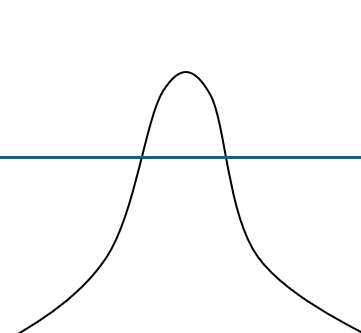
超过饱和线的部分不会被吸收，而饱和线以下的部分则会被吸收一部分，导致展宽下降