TD 4:Drude模型,电导率,电流,复介电常数,折射率和消光系数
TD 4:Drude模型,电导率,电流,复介电常数,折射率和消光系数

电场环境,半-自由电子,没有相互作用,电子平均\(\tau\)秒碰撞一次

- Drude运动方程,受力被视为阻力
\[ \frac{d^2\vec x}{dt^2}m_e = -e\vec E-\frac {m_e}\tau\frac{d\vec x}{dt} \]
- \(\vec x\)满足 \(\vec x = \vec x_0e^{i\omega t}\),得到:
\[ -\omega^2\vec x+i\frac{\omega}\tau\vec x = -\frac{e}{m_e}\vec E \Rightarrow \vec x_0 = \frac{e\vec E_0}{(\omega^2-i\frac \omega\tau)m_e} \]
- 注意这里题目要求实际上质量要写作\(m\)

- 电流:
\[ \vec J(\omega) = N.(-e).\frac{d\vec x}{dt} = \frac{-ie^2N\omega}{(\omega^2-i\frac\omega\tau)m_e}\vec E = \frac{e^2N}{(i\omega+\frac1\tau)m_e}\vec E \]
- 电导率:
\[ \sigma(\omega) = \frac{\vec J(\omega)}{\vec E(\omega)} = \frac{e^2N}{(i\omega+\frac 1\tau)m_e} \]
- 若电导率:
\[ \sigma_0 = \sigma(0) = \frac{e^2N}{\frac 1\tau m_e} = \frac{e^2\tau N}{m_e} = 5.9\times10^{-7}\Omega^{-1}m^{-1} \]
- 则平均碰撞时间:
\[ \tau = \frac{\sigma_0m_e}{e^2N} = 2.6\times10^{-14}s \]
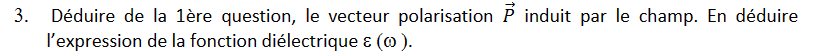
\[ \vec P = N\vec p = -e.N.\vec x = -e.N.\frac{e\vec E}{(\omega^2-i\frac \omega\tau)m_e} = -\frac{e^2N\vec E}{(\omega^2-i\frac \omega\tau)m_e} \]
\[ \vec D = \varepsilon_0\vec E +\vec P = (1-\frac{e^2N}{(\omega^2-i\frac \omega\tau)\varepsilon_0m_e})\varepsilon_0\vec E \]
- 得到介质介电常数:
\[ \varepsilon = 1-\frac{e^2N}{(\omega^2-i\frac \omega\tau)\varepsilon_0m_e} \]
- 设:\(\omega_p^2 = \frac{Ne^2}{m\varepsilon_0}\),得到:
\[ \varepsilon = 1-\frac{\omega_p^2}{\omega^2-i\omega/\tau} = 1-\frac{\omega_p^2\omega^2}{\omega^4+\omega^2/\tau^2}+i\frac{\omega_p^2\omega/\tau}{\omega^4+\omega^2/\tau^2} = 1-\frac{\omega_p^2\tau^2}{\omega^2\tau^2+1}+i\frac{\omega_p^2/\tau}{\omega^3+\omega/\tau^2} \]

\(0<\omega<1/\tau:\)
\[ N' = 1-\omega_p^2\tau^2, N'' = \omega_p^2\tau/\omega,\ \ |N''|\gg|N'|\Rightarrow \varepsilon = i\omega_p^2\tau/\omega \]
- 考虑折射率和复介电常数关系:\(N' =n^2-\kappa^2,\ \ N'' = 2n\kappa\)
- 得到:\(n^2 = \kappa^2,n = \kappa = \frac{N''}2 = \omega_p\sqrt{\frac{\tau}{2\omega}}\)
- 穿透深度:\(\delta = \frac{c}{\omega \kappa}\) = \(\frac c{\omega\omega_p} \sqrt{\frac {2\omega}\tau}\)
\(1/\tau < \omega <\omega_p\):
\[ N' = 1-\omega_p^2/\omega^2, N'' = \omega_p^2/\omega^3\tau,\\\ \ |N''|\ll|N'|\Rightarrow \varepsilon = 1-\omega_p^2/\omega^2 = -\omega_p^2/\omega^2 \]
- 考虑折射率和复介电常数关系:参考第四章相应内容
- \(n ^2 = \frac{N’+|N’|}{2} = 0\),\(k^2 = \frac{|N’|-N’}{2} = \omega_p^2/\omega^2\)
- 穿透深度:\(\delta = \frac{c\omega}{\omega_p^2}\)
\(\omega_p<\omega:\)
\[ N' = 1, \ \ N'' = 0\Rightarrow n = 1,\ \ k = 0,\ \, \delta = \infty \]