TD 3：模式频率，模式频率间隔，有折射率导致的能量衰减，高斯光束

• \(\nu_m = m(\frac{c}{2nL})\)
• \(\Delta \nu_c = \frac{c}{2nL} = 8.54\times10^8s^{-1}\)
• \(m = \frac 1T\frac 1{\Delta\nu_c} = \frac {c}{\lambda}\frac 1{\Delta\nu_c} = 329929.5\approx 329930\)
• \(\nu_m = 329930\Delta\nu_c =2.818\times10^{14}Hz\)

• \(Q = mF = m\frac{\pi\sqrt{R_e}}{1-R_e}\)
• \(R_e = \sqrt{R_1R_2}e^{-\alpha L}\)

接下来从复折射率转换到吸收系数\(\alpha\)：

• 复折射率：\(\widetilde w = n-i\kappa\)
• 考虑电场：\(\vec E = E_0e^{i(\omega t-kz)} = E_0e^{i(\omega t-\frac \omega cn z)}e^{-\frac \omega c \kappa z}\vec e_z\)
• 能量强度：\(I = |E_0|^2e^{-\frac {2\omega \kappa z}{c}}\)
• 得到：\(\alpha = \frac{2\omega\kappa}{c} = \frac{4\pi\kappa}{\lambda} = 0.0118\)

继续计算：

• \(R_e = 0.995\cdot e^{-\frac{4\pi\kappa L}{\lambda}} = 0.9938,\ \ Q = 1.67\times 10^{8}\)
• \(\tau_c = \frac{Q}{\omega}= \frac{Q\lambda}{c2\pi} = 9.444\times10^{-8}s\)

• 高斯光束：\(I = I_0e^{-a(\nu-\nu_0)^2}\)
• 计算\(a\)与\(\Delta\nu\)的关系：在\(\nu_0\pm\frac{\Delta\nu}2\)的范围内，光强等于\(I_0\frac 1{e^2}\):

\[ I_0e^{-a\frac{\Delta\nu^2}{4}} = I_0\frac 1{e^2}\Rightarrow a = \frac{8}{\Delta\nu^2} \]

• 已知\(\Delta \lambda\)，考虑\(\Delta \nu\)与\(\Delta \lambda\)的关系：

\[ \nu = c/\lambda\Rightarrow\Delta\nu = \frac c{\lambda^2}\Delta\lambda = \frac{c}{(1.064\times10^{-6})^2}0.1\times10^{-10} = 2.65GHz \]

• 注意这里\(Å\)代表埃米，是\(10^{-10}m\)
• 计算模式间距\(\Delta\nu_c\)：\(\nu = m\times\Delta\nu_c\)
• 注意区分模式间距和光束宽度
• 光强表达式转换为：

\[ I = I_0e^{-8(\frac{\Delta\nu_c}{\Delta\nu})(m-m_{\nu_0})^2} > I_0\frac 1{e^2}\Rightarrow-8(\frac{\Delta\nu_c}{\Delta\nu})^2(m-m_{\nu_0}) \ge -2 \]

• 得到可选模数：\(329886,329887,329888\)
• 反推频率

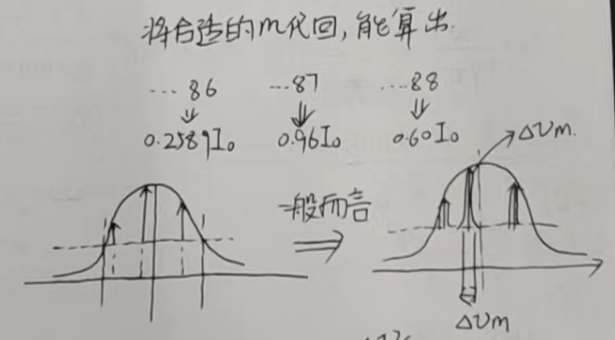
• 损耗导致的峰变宽：\(\Delta\nu_m = \frac {\Delta \nu_c}F\)
• 最后考虑到激光的偏振状态，最终模数为\(2\times3 = 6\)