TD2：光栅，傅里叶光学

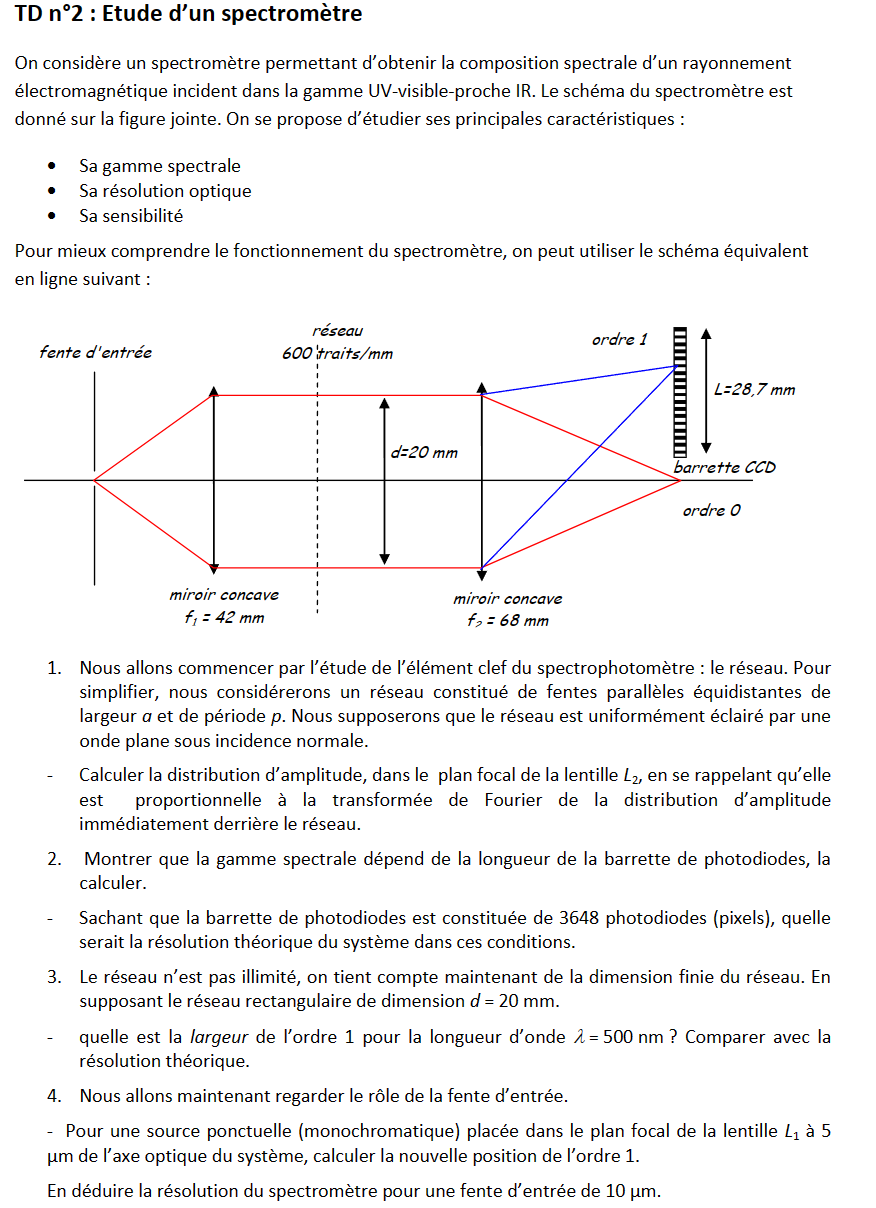
假设光栅是无限长的，周期为p，单个周期的通过长度为a，【光栅到屏幕的距离可以视为镜二的焦距的二倍】计算屏幕上的强度分布：
- 通过光栅的光可以视为：\(f(x) = Rect(\frac x a)\otimes \sum\delta(x-np)\)
- 其傅里叶变换为：\(\widehat f(k_x) = asinc(ak_x)\cdot\frac 1 p \sum \delta(k_x-\frac n p)\)
- 转换到屏幕所在面坐标：\(c \widehat f(x') = asinc(a\frac{x'}{2\lambda f_2})\cdot\frac 1 p \sum \delta(\frac{x'}{2\lambda f_2}-\frac n p)\)
- 由于强度分布正比于傅里叶变换，存在k，使得：
  
  \[ A_p = kasinc(a\frac{x'}{2\lambda f_2})\cdot\frac 1 p \sum \delta(\frac{x'}{2\lambda f_2}-\frac n p) \]
- 公式中n代表模态，比如第零模态出现在\(x' = 0\)，之后每个模态之间差\(\frac{2\lambda f}{p}\)
屏幕总长度为L = 28.7nm，总像素数3648个
- 研究其能显示的波长范围和最小波长分辨率
- 波长范围跟L相关，对于第一级，\(x' = \frac{2\lambda f_2}{p}\)，求\(L= \frac{2\Delta\lambda f_2}{p}\Rightarrow\Delta\lambda = \frac{Lp}{2f_2} = 7034.3nm\)
- 最小分辨率：\(\frac{\Delta\lambda}{3648} = 1.93nm\)
考虑光栅长度为d = 20mm，计算新的强度分布：
- 在这种情况下，\(f(x) = Rect(\frac x d) \cdot[ Rect(\frac x a)\otimes \sum\delta(x-np)]\)
- 计算傅里叶变换之后：\(\widehat f(k_x) = dsinc(dk_x) \otimes [asinc(ak_x)\cdot\frac 1 p \sum \delta(k_x-\frac n p)]\)
  
  \[ A_p = kdsinc(d\frac{x'}{2\lambda f_2}) \otimes [asinc(a\frac{x'}{2\lambda f_2})\cdot\frac 1 p \sum \delta(\frac{x'}{2\lambda f_2}-\frac n p)] \]
- 此时的条纹总宽度：\(\frac{4\lambda f_2}{d}\)， \(\Delta x' = \frac{2\lambda f_2}{d} = 3.4\mu m\)
- 注意，\(sinc(\pm 1) = 0\)，这对应着条纹宽度
- 而屏幕的长度分辨率：\(\Delta x = \frac {28.7}{3648} = 7.87\mu m > \Delta x'\)
- 所以，考虑光栅宽度导致的展宽提升并不会反映在屏幕上
由光源本身宽度导致的展宽提升体现在x的偏移上，例如在\(x_{optique,0} = 5\mu m\)时，经过两个透镜的放大，最终体现在屏幕上：
- \(\Delta x'_0 = \frac {x_{optique,0}}{42}\times68 = 8.1\mu m\)
- 最终的展宽：\(\Delta x_{final} = 2\Delta x'_o+\Delta x' = 19.6\mu m>7.87\mu m\)