Cours 6:激光
Cours 6:激光
激光
激光的历史和描述

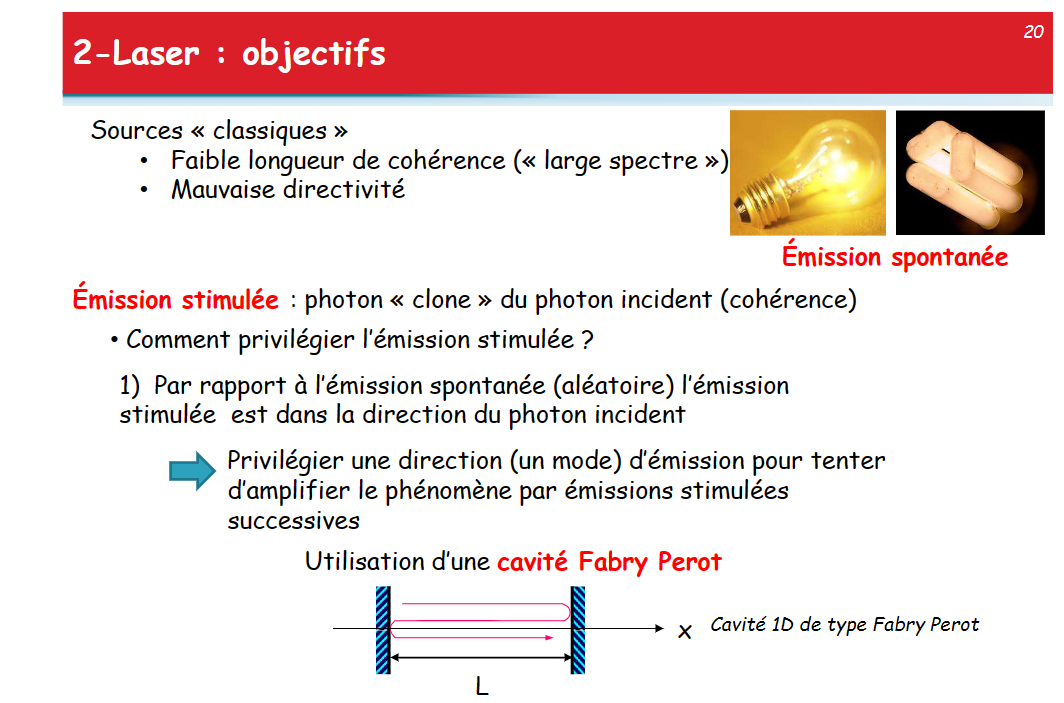
- 传统光源相关长度小,光谱;方向性差
基本原理:受激辐射&电子数反转
受激辐射本身有良好的相关长度和单色性
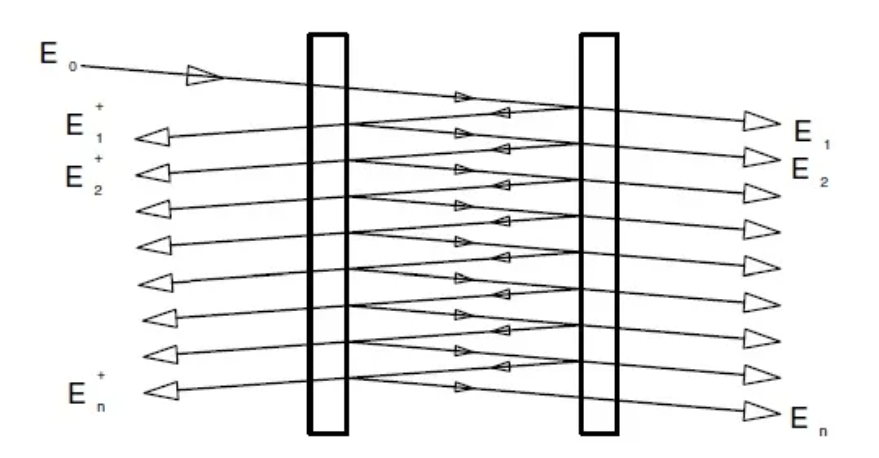
优先考虑发射方向(模式),以尝试通过连续受激辐射放大现象:使用cavité Fabry Perot【法布里-珀罗腔】
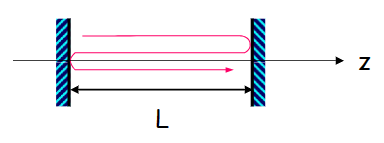
这里我们考虑一维共振腔,即入射光垂直于镜面
为了能够使受激辐射出的光子大于用于照射的光子数量,需要电子数的反转。也就是高能级电子数多于低能级电子数。
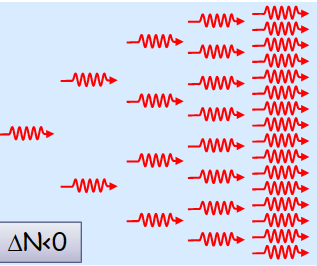
共振腔
传播方程和解
传播方程:\(\vec \Delta \vec E -\frac \varepsilon {c^2}\frac{\partial^2\vec E}{\partial t^2} = 0\)
考虑驻波:\(E(z,t) = f(z)\chi(t)\)
得到新的方程:
\[ \begin{cases}\chi(t) = Aexp(-i(\omega t+\varphi)) \\ \frac{\partial^2\vec f(z)}{\partial z^2}+\frac{\varepsilon\omega^2}{c^2}f(z) = 0\end{cases} \]
考虑初始条件:\(f(0) = f(L) = 0\)
解得:\(f(z) = f_0sin(k_Pz)\quad avec \quad k_p = p \frac \pi L\)
最终得到空腔内电场空间分布:
\[ f_p(z) = f_0sin(p\frac\pi Lz) \]
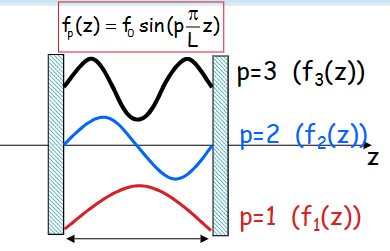
色散关系,\(k_p,\nu_p,\lambda_p\)
- \(k_p = p \frac \pi L = \sqrt{\varepsilon}\frac {\omega_p} c = n\frac{2\pi\nu_p}{c} = n\frac{2\pi}{\lambda_p}\)
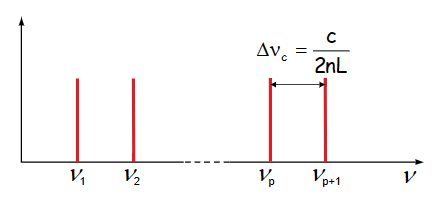
- \(\nu_p = p\frac c{2nL}\)
- \(\lambda_p = \frac {2nL}{p}\)
- 其中,n为空腔内折射率,p为模态数
- 两模态间距:\(\Delta\nu_c = \frac c {2nL}\)
真实情况:考虑输入,输出
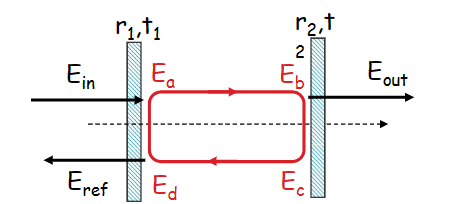
\[ \begin{split}&E_a = t_1E_{in}+r_1E_d\\&E_b = E_aexp(ikL)\\&E_c = r_2E_b\\&E_d = E_cexp(ikL)\end{split} \]
- 注意这里\(E_c\)的表达,由于r已经是比例系数,不需要减去出射的部分
- 得到输出:
\[ E_{out} = E_bt_2 = t_1t_2E_{in}e^{ikL}\frac 1{1-r_1r_2e^{2ikL}}\quad avec \quad k = p \frac \pi L \]
- 再另一种情况中,光源在共振腔内部产生,此时:\(E_a= r_1+E_0\)
- 修改公式有:
\[ E_{out} = E_bt_2 = t_2E_{0}e^{ikL}\frac 1{1-r_1r_2e^{2ikL}}\quad avec \quad k = p \frac \pi L \]
考虑损耗
认为除了镜面反射的损耗\(r_1,r_2\),在传播过程中会有吸收和散射导致的损耗【Loi de Beer-Lambert】
- \(u(z) = u_0e^{-(\alpha_{abs}+\alpha_{diff})z}(r_1r_2)^2 = u_0e^{-\alpha_{eff}z}\quad avec \quad \alpha_{eff} = \alpha_{abs}+\alpha_{diff}+\frac 1Lln(\frac 1 {r_1r_2})\)
- 体现在电场中,有:
- \(E_b = E_aexp(ikL)exp(-\frac {(\alpha_{abs}+\alpha_{diff}) L} 2)\)
- \(E_d = E_cexp(ikL)exp(-\frac {(\alpha_{abs}+\alpha_{diff}) L} 2)\)
- 除以二的原因使上式是能量关系
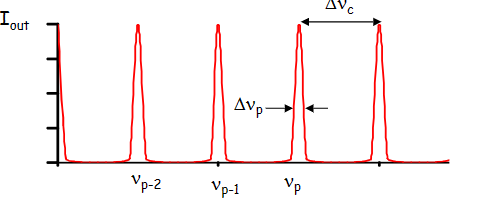
- 真实情况导致缝宽的出现Élargissement des pics
- 最终得到输出:
\[ E_{out} = t_2e^{ikL}\frac 1{1-r_1r_2e^{-(\alpha_{abs}+\alpha_{diff})L}e^{2ikL}}E_{0}\\I_{out} = \frac{T_2I_0}{(1-r_1r_2e^{-(\alpha_{abs}+\alpha_{diff})L})^2+4r_1r_2e^{-(\alpha_{abs}+\alpha_{diff})L}sin^2(\pi\nu\frac {2L}c)} \]
- T 代表强度(能量)的透射系数,见第4章最后
品质因子
\(Q_p = \frac{\nu_p}{\Delta \nu_p} = \frac {2\pi}{T_p}\frac u{|du/dt|}\)
- 这里的\(T_p\)是周期
- 其中\(|du/dt|\)代表周期能量损失:\(|du/dt| = |\frac{du}{dz}\frac{dz}{dt}| = \alpha_{eff}u\frac cn\)
- 得到:\(Q_p = \frac {2\pi}{T_p}\frac n{c\alpha_{eff}}\)
- 又因为:\(\frac{2\pi n}{T_pc} = \frac{\omega_pn}{c} = k_p = \frac{2\pi n}{\lambda_p}\)
- 得到:\(Q_p = \frac{2\pi}{\lambda_p}\frac{nL}{\alpha_{abs}L+\alpha_{diff}L-ln(r_1r_2)}\)
- 又因为:\(u = u_0e^{-t/\tau_p}\)
- 得到:\(Q_p =\frac{2\pi}{T_p}\tau_p = \omega_p\tau_p\)
\(Q_p = \frac{\nu_p}{\Delta \nu_p} = \frac {2\pi}{T_p}\frac u{|du/dt|}= \frac {2\pi}{T_p}\frac n{c\alpha_{eff}}= \frac{2\pi}{\lambda_p}\frac{nL}{\alpha_{abs}L+\alpha_{diff}L-ln(r_1r_2)}=\frac{2\pi}{T_p}\tau_p = \omega_p\tau_p\)
持续时间(Durée de vie)和平均移动距离(Parcours moyen)
- Durée de vie:\(\tau_p = \frac{Q_p}{\omega_p}\)
- Parcours moyen:\(L_p = \frac cn\tau_p = \frac 1{\alpha_{eff}}\)
活性介质
激光要求电子数反转
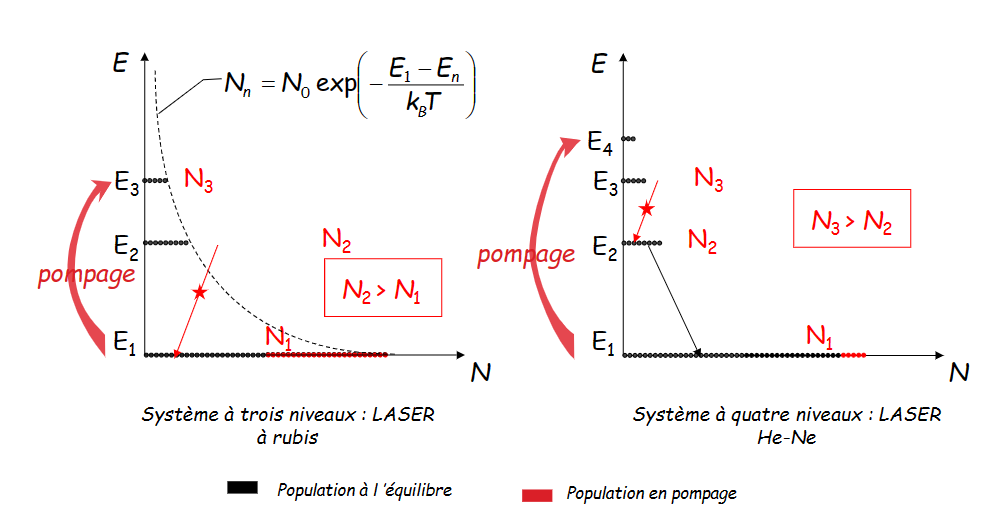
电子数变化:以\(\tau\)表示自发辐射

- R代表从高能级向能级2跃迁的电子数
- \(-\frac {N_1}{\tau_1}\)代表从能级1向更低能级的跃迁
- 平衡时,认为\(-W_{12}N_2+W_{12}N_1 = 0\)
- \(W_{12} = B_{12}u(\nu_{12})g(\nu_{12})\)
- 根据平衡\(dN_i/dt= 0\):
\[ R = \frac {N_2}{\tau_2}, \ \frac{N_1}{\tau_1} = \frac{N_2}{\tau_{21}},\quad \Delta N_0 = N_2-N_1 = \tau_2R-\frac{\tau_1\tau_2}{\tau_{21}}R = R\tau_2(1-\frac{\tau_1}{\tau_21}) \]
- 在有入射光的情况下:\(-W_{12}N_2+W_{12}N_1 \ne 0\)
- 根据相同的方法,根据平衡\(dN_i/dt= 0\):
\[ \Delta N = \frac{\Delta N_0}{1+\tau_{s}W_{12}}\quad avec \quad\tau_s = \tau_2+\tau_1(1+\frac{\tau_2}{\tau_{21}}) \]
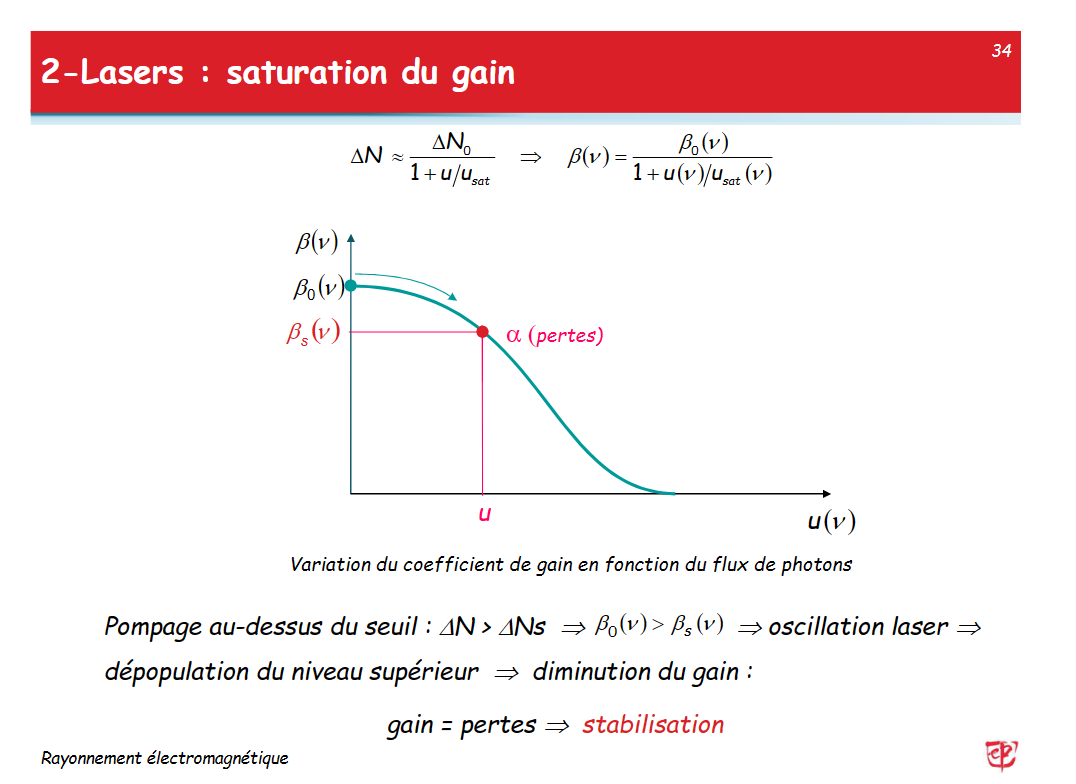
- 设能量\(u_{sat} = \frac 1{\tau_sB_{12}},\)则有:\(\Delta N = \frac{\Delta N_0}{1+u/u_{sat}}\)(忽略\(g(\nu)\))
放大增益
\(du_1 = \beta(\nu)u_1dz\)
- \(\beta(\nu) = \frac{nh\nu}cB_{12}g(\nu)\Delta N = \sigma(\nu)\Delta N\)
- \(\beta(\nu) =\frac{\beta_0{\nu}}{1+u(\nu)/u_{sat}(\nu)}\)
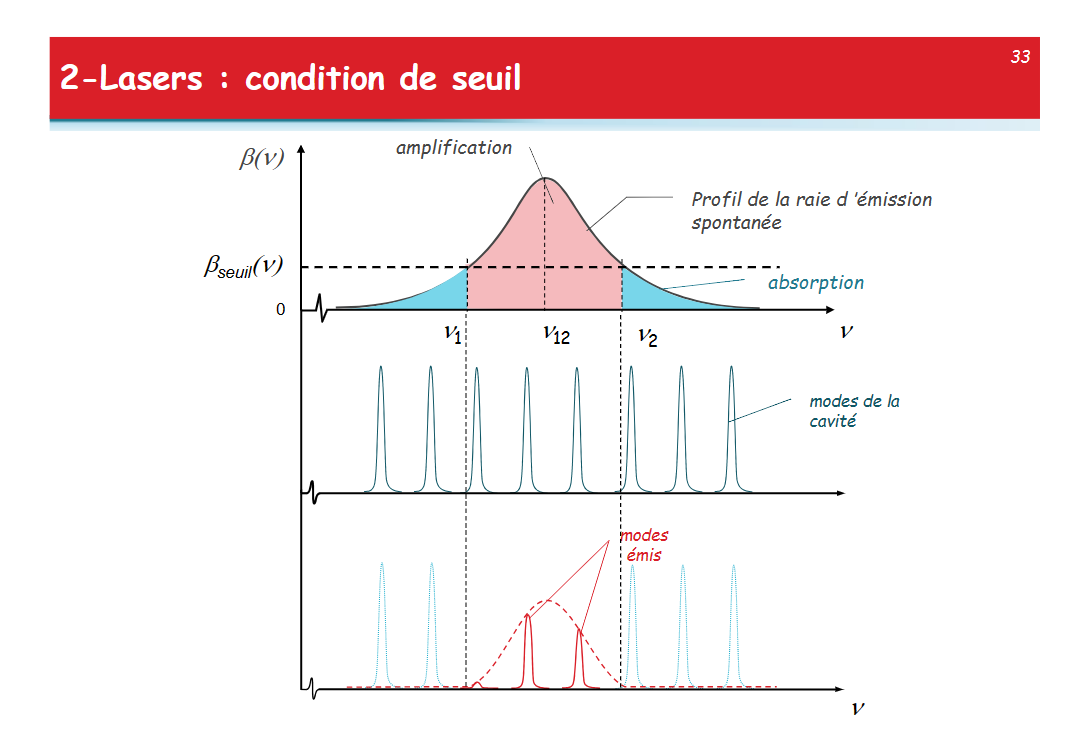
增益阈值
- 能量损失:\(du_2 = -\alpha_cu_2dz\)
- 若使激光器输出,须有:\(\beta_s-\alpha_c = 0\)
- 带入电导率:
\[ \beta_s = \frac{n\lambda^2}{8\pi\tau_{sp}}\frac 1{\Delta \nu}\Delta N_s \]
- 这里\(\tau_{sp}\)是自发辐射时间,见第五课,爱因斯坦系数
粒子数阈值
- 带入吸收系数:\(\beta_s=\alpha_c = \frac{\omega}{cQ} = \frac{1}{c\tau_c}\),这里的\(\tau_c\)等价于在本节课笔记中的品质因子节中的\(\tau_p\)
\[ \Delta N_s = \frac{8\pi \tau_{sp}\Delta\nu}{n\lambda^2c\tau_c} \]