Cours 5:光与物质相互作用的量子描述和半经典描述
Cours 5:光与物质相互作用的量子描述和半经典描述
11月14日,没有带笔记本,故发现电子笔记远胜于纸质笔记

Révision: 对于使用经典力学的处理方法
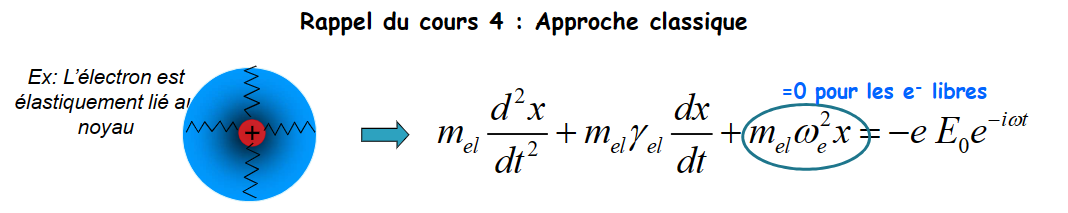
- 对于dielectrique的阻尼震动模型 \(m_e\frac {d^2x}{dt^2} = -kx\)
- 对于金属(metaux)的Drude模型 \(m_e\frac{d^2x}{dt^2}+m_e\gamma_e\frac{dx}{dt} = -eE_0e^{i\omega t}\)
- 电磁波的散射:瑞利散射,共振或者汤姆森散射 [小于,接近,大于]
这些方法忽略的量子性
原子,分子和固体的量子描述
孤立原子-离散能级
薛定谔方程
\[ [-\frac{ℏ}{2m_e}\Delta + V(r)]\phi = E\phi \]
- n :主量子数
- l:轨道量子数[0, 1, …, n-1]
- m:磁量子数 \(\pm l\)
双原子分子
震动-谐振子模型
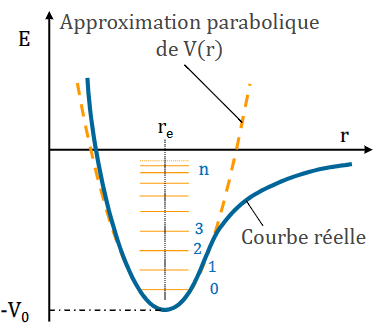

量化的势阱中粒子能量
\[ E_n = (n+\frac{1}{2})\hbar\omega, n = 0,1,2,... \]
弹性系数k:
\[ \nu = \frac{1}{2\pi}\sqrt{\frac{k}{\mu}},\quad \mu = \frac{m_1m_2}{m_1+m_2} \]
E ~ 1 eV gamme des proches IR
转动-刚性旋转器(de moment d ’inertie I)
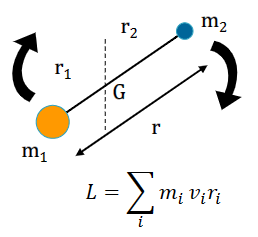
围绕重心的转动动能
\[ E_c = \frac12I\omega^2 = \frac{L^2}{2I} = \frac{L^2}{2\mu r^2}, \\ \mu = \frac{m_1m_2}{m_1+m_2} \]
动量模量的量化
\[ E_l = \frac{l(l+1)\hbar^2}{2I}\\ \Delta E = E_l-E_{l-1} = l\frac{\hbar^2}{l} \]
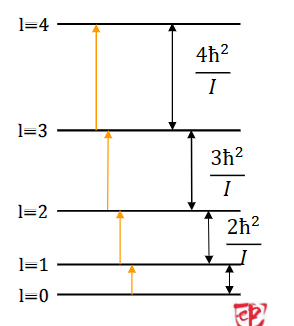
E ~ 0,001 - 0,01 eV gamme des IR lointains
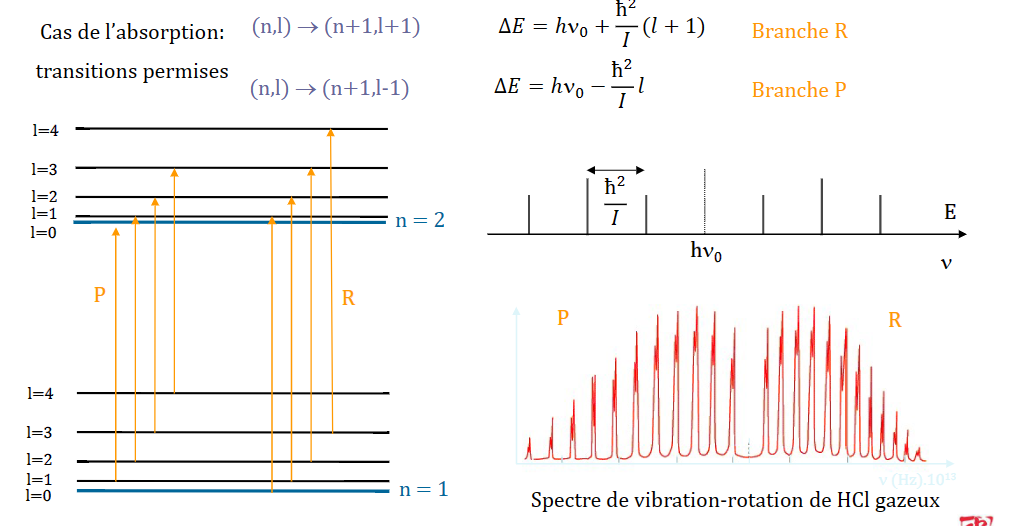
结合转动和平动
\[ E = -V_0+(n+\frac12)hv+\frac{l(l+1)\hbar^2}{2I} \]
SOlIDE 固体
能带
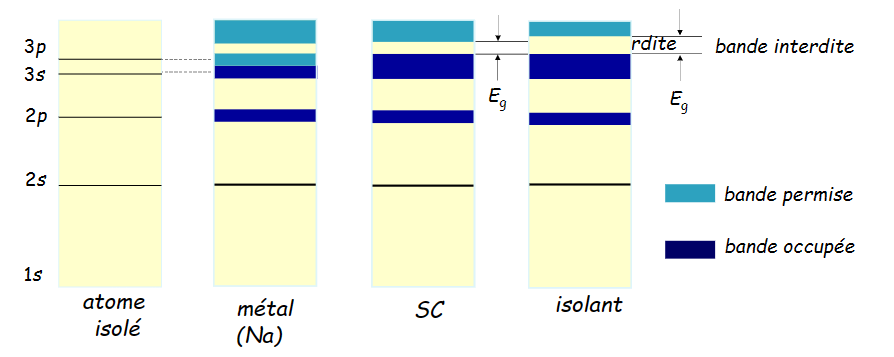
- bande occipée: 满带,被电子填满
- bande permise: 导带或者空带
- bande interdite: 带隙
光子(不明作用)

半经典方法
在量子描述中,场和物质都被量化,而在半经典描述中,仅有物质被量化

这些能级可能是电子你呢合计,也可能是震动,旋转能级
玻尔兹曼分布
\[ \frac{N_2}{N_1} = exp[-\frac{E_2-E_1}{kT}] \]
原子-光子相互作用
自发辐射 Émission spontanée
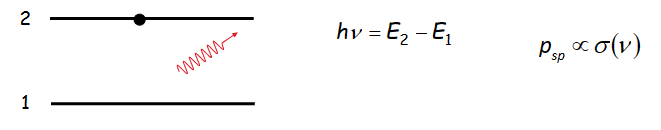
辐射能量为 \(hv = E_2-E_1\), 辐射概率 \(p_{sp}\)正比于电导率 \(\sigma\)
单位时间内,辐射的原子数 \(\delta N = -p_{sp}N\delta t\), 得到
\[ N= N(0)exp(-t/\tau) \quad avec \quad \tau_{sp} = p^{-1}_{sp} \]
自发辐射发生在各个方向
吸收 Absorption
- 对于单个电子,吸收能量为\(hv = E_2-E_1\),辐射概率 \(p_{ab}\)正比于电导率 \(\sigma\)
- 对于n个光子,taux de probabilité 吸收概率: \(P_{ab} = np_{ab} = w_{12}\)
- 对于N个基态原子,单位时间内辐射数\(\delta N = -w_{12}N\delta t\)
受激辐射 Émission stimulée
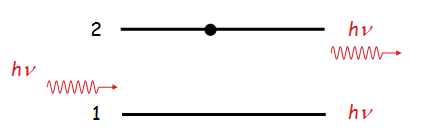
- 对于n个光子,\(P_{st} = np_{st} = w_{21}\)
- 概率\(p_{st}\)正比于\(\sigma\)
- 被激发的光子是原光子的克隆
- 注意这里强调的是从2到1的过程,这个过程需要光的激发才能完成

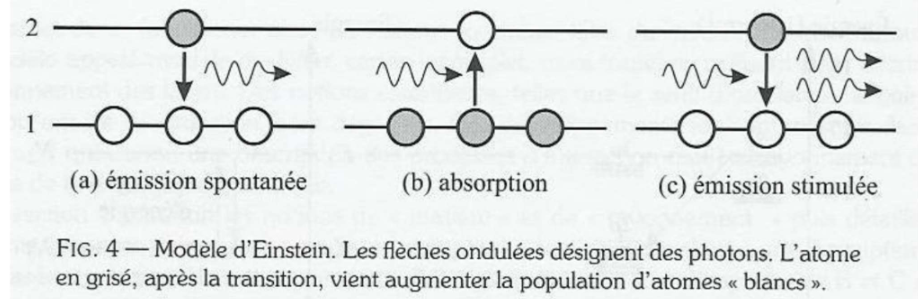
光谱
孤立原子的辐射过程
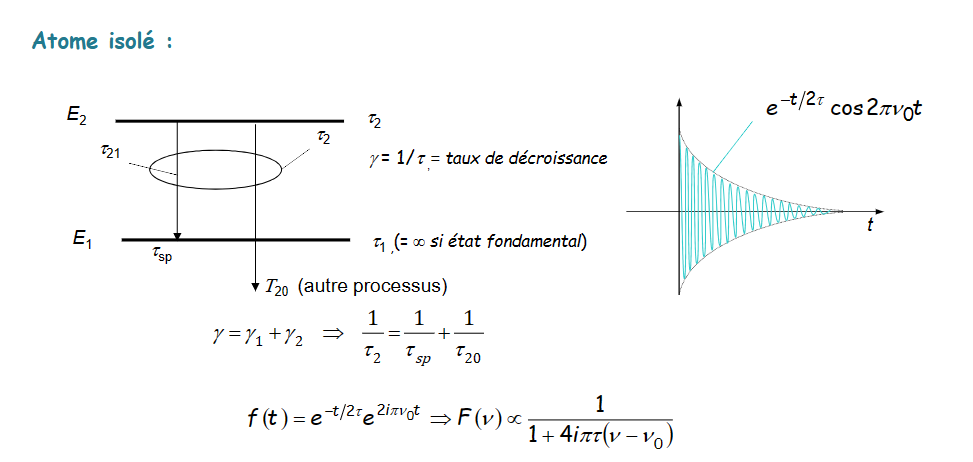
- 辐射过程包括从2到1的辐射和从2到0的辐射
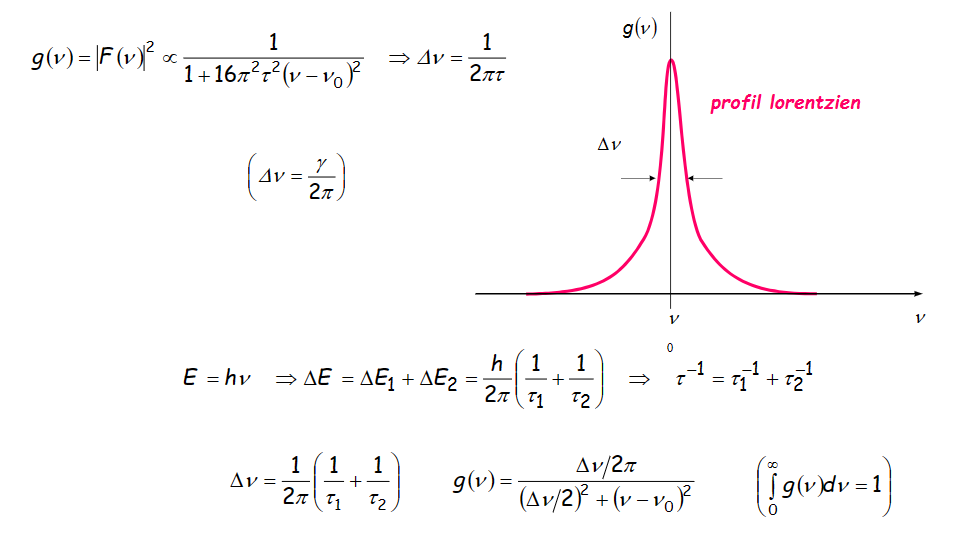
- \(\Delta \nu\)是\(g(V)\)取到1/2位置的v的2倍
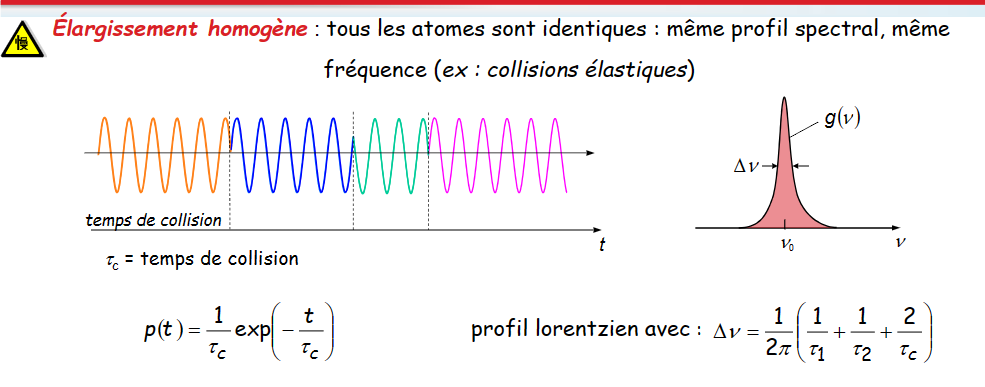
均匀放大 Élargissemnet homogène
所有原子相同:相同的光谱分布,相同的频率(如弹性碰撞)
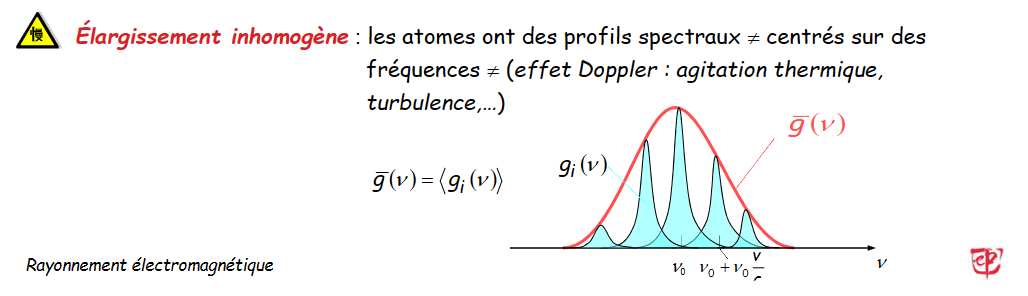
非均匀放大 Élargissement inhomogène
原子具有以频率为中心的光谱分布(多普勒效应:热搅拌、湍流等)
爱因斯坦参数
Hypothèse: interactions entre une onde polychromatique et une collection d’atomes identiques avec
爱因斯坦假设
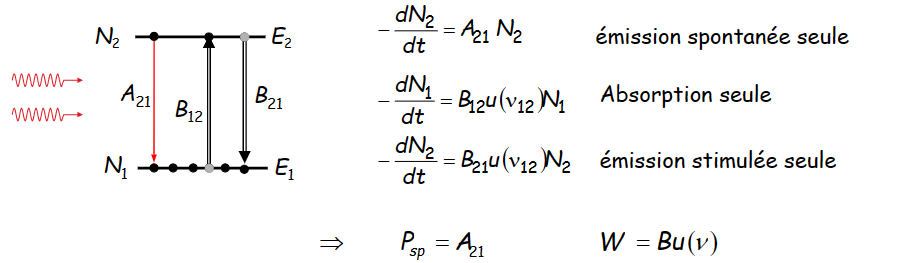
结合电子量守恒\(\frac{dN_2}{dt} = -\frac{dN_1}{dt}\)
得到总的电子变换方程:
\[ \frac{dN_2}{dt} = B_{12}u(\nu_{12})N_1 -B_{21}u(\nu_{12})N_2-A_{21}N_2 \]
平衡时,\(\frac{dN_2}{dt} = 0 \Rightarrow u(\nu_{12}) = \frac{A_{21}/B_{21}}{B_{12}N_1/B_{21}N_2-1}\)
结合开头提到的玻尔兹曼方程:\(\frac{N_2}{N_1} = exp[-\frac{E_2-E_1}{kT}]\),得到:
\[ u(\nu_{12}) = \frac{A_{21}/B_{21}}{B_{12}/B_{21}exp(h\nu_{12}/kt)-1} \]
结合普朗克方程:\(u(\nu) = \frac{8\pi h\nu^3/c^3}{exp(h\nu/kT)-1}\)推得:
\[ B_{12} = B_{21}\quad et \quad A_{21}/B = 8\pi hv^3/c^3 = 8\pi h/\lambda^3 \]
得到结论:
\[ p_{sp} = A_{21} = \tau_{sp}^{-1}\\W_{12} = W_{21} = \frac{\lambda^3}{8\pi h\tau_{sp}}u(\nu) \]
单色光和多色光情况
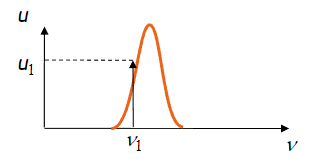
由于能级本身具备一些宽度\(\Delta\nu_{at}\),如果光源不能覆盖整个能级的宽度,则需要做一些修正
- 对于单色光,\(W = Bug(\nu_1)\)
- 对于多色光,\(W= \int_{\Delta \nu}Bug(v)dv\)
- 如果\(\Delta \nu > \Delta \nu_{at},\)则能全部覆盖能级,此时不需要乘以\(g(\nu)\)
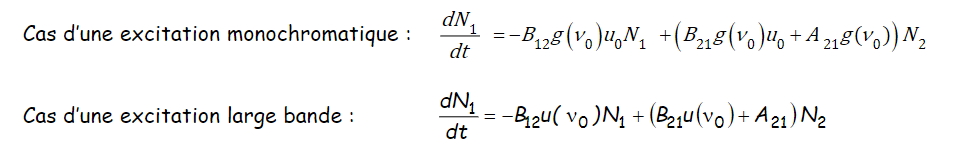
能量的吸收和释放
在计算能量的吸收时,由于入射光本身是有方向的,所以不考虑自发辐射的无向光输出
\[ \frac{du(\nu,t)}{dz} = \frac{du(\nu,t}{dt}\frac{dt}{dz} = -[h\nu B_{12}g(\nu)N_1-hvB_{21}g(\nu)N_2]u(\nu,z)n\frac{1}{c} \]
得到吸收率:\(\alpha(\nu) = \frac{h\nu n}{c}B_{21}g(\nu)[N_1-N_2] = \frac{h\nu n}{c}B_{21}g(\nu)[\Delta N]\)
- 吸收:\(\Delta N>0\)
- 辐射:\(\Delta N <0\)
剩余内容
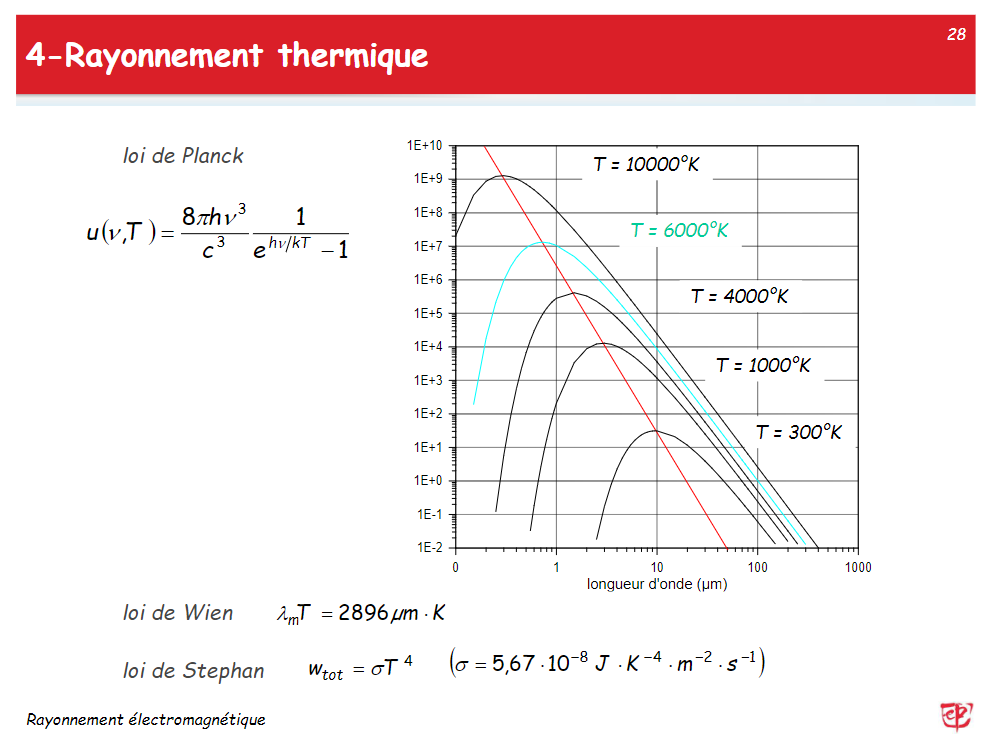
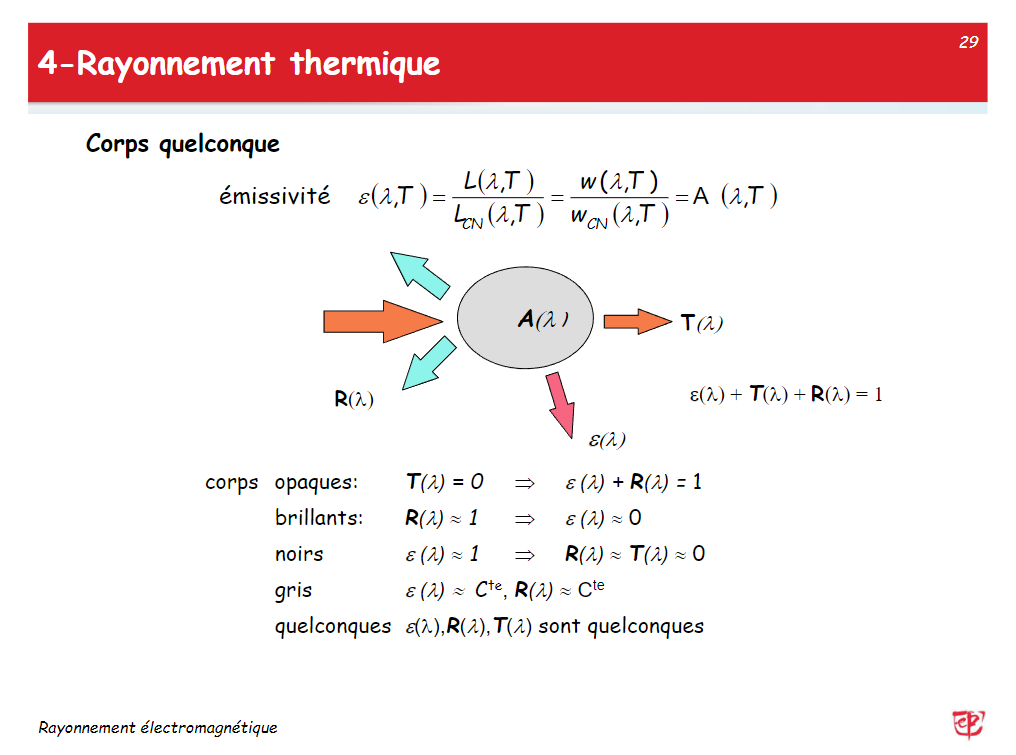
热辐射
发光
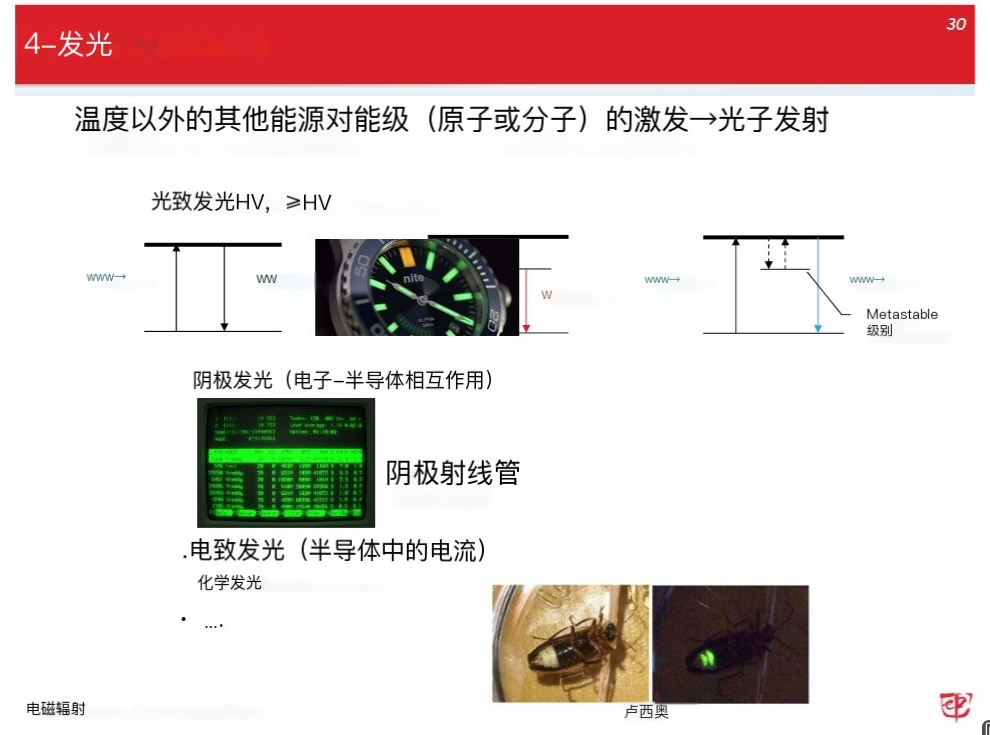
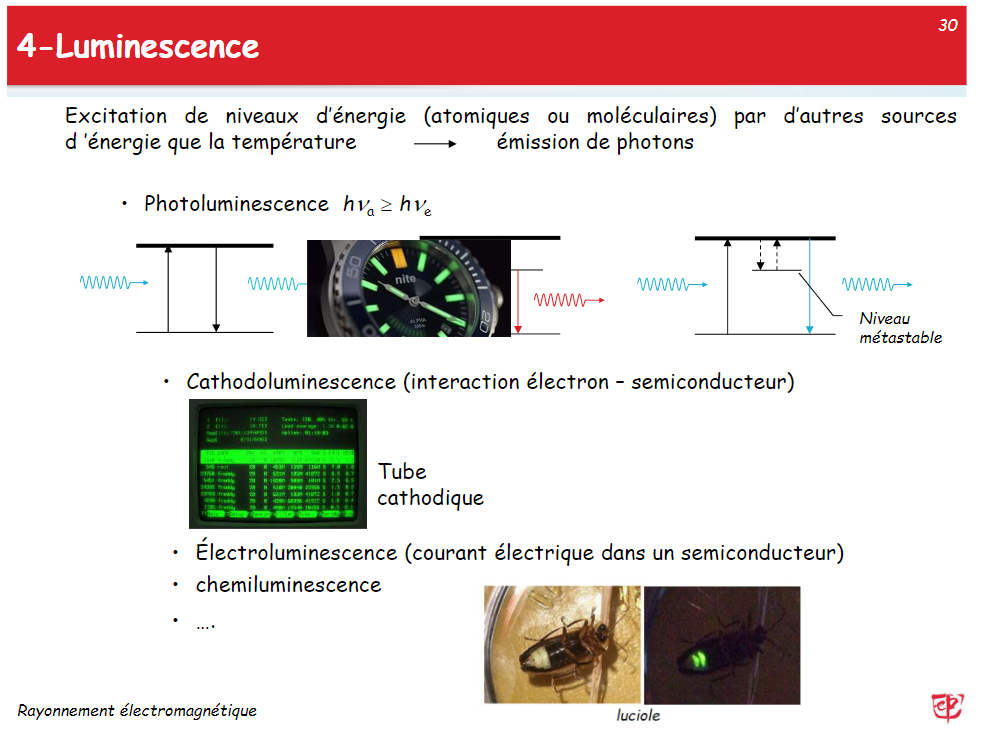
荧光和磷光
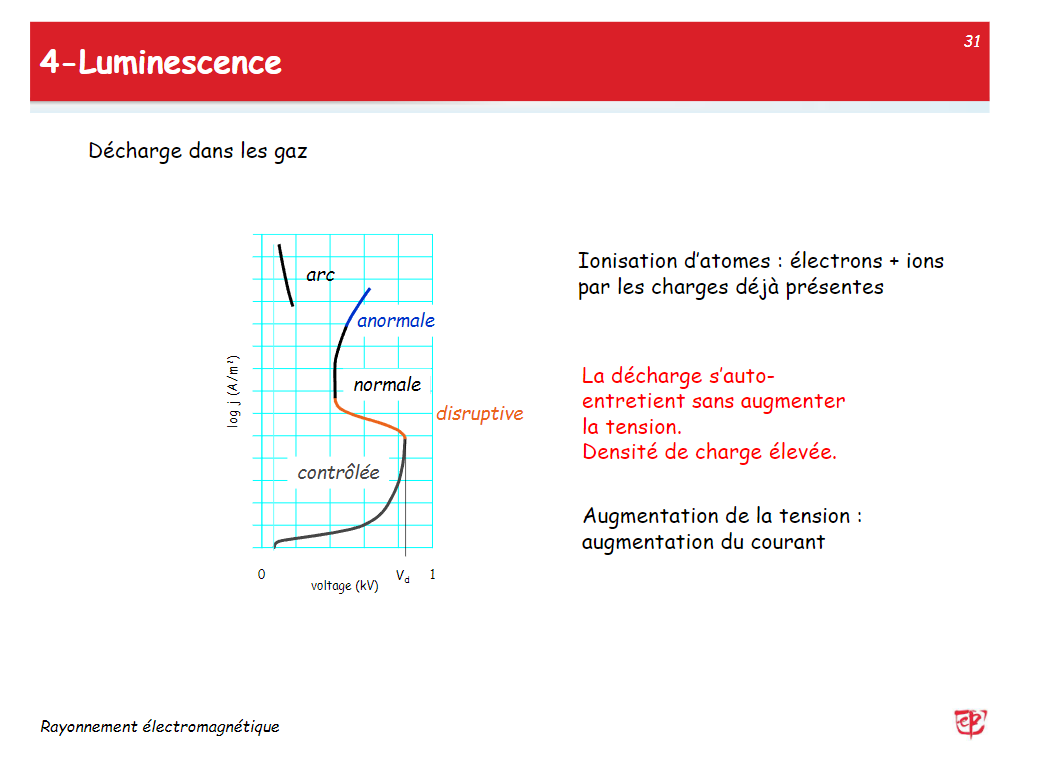
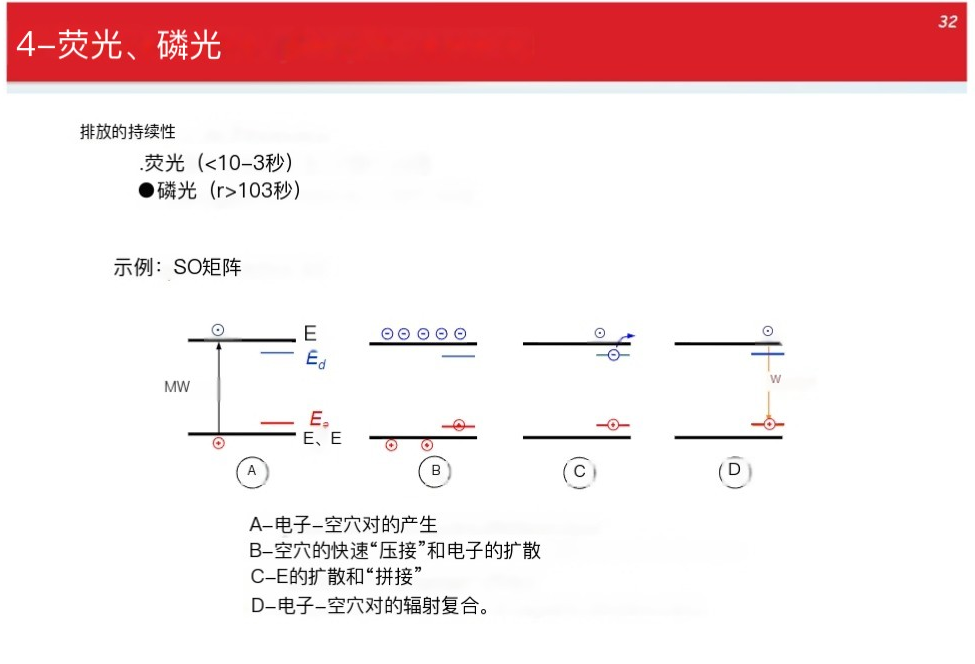
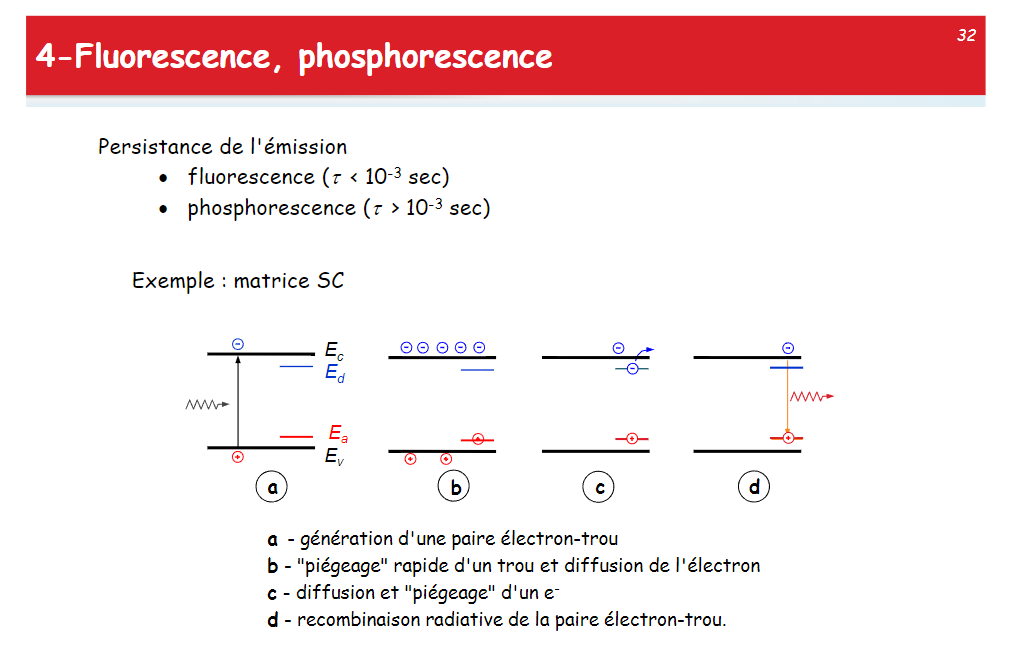
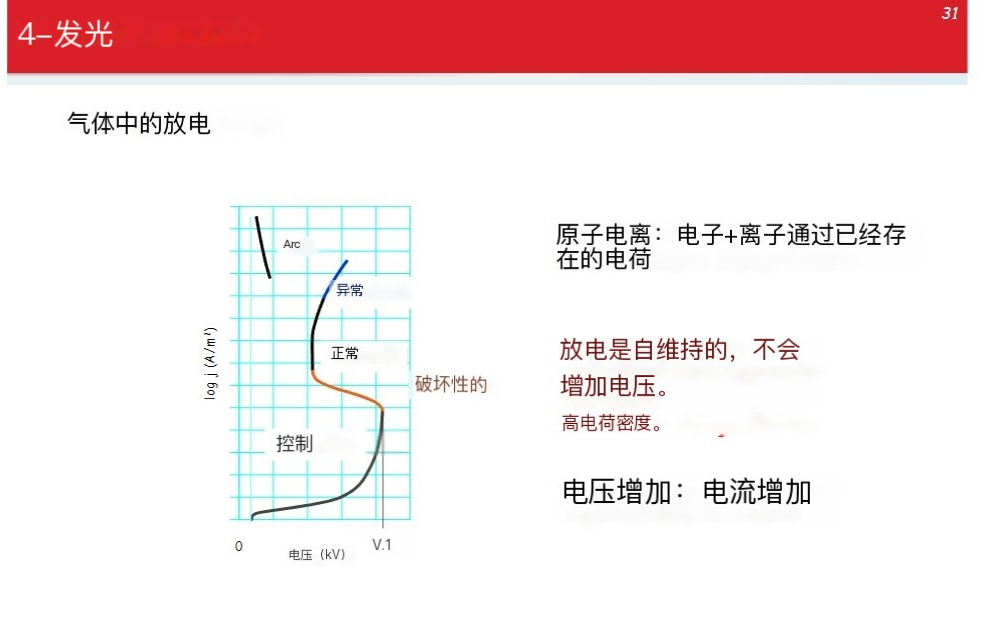
光源