Cours 4 射线-物质相互作用:传统方法,折射率和复介电常数
Cours 4 射线-物质相互作用:传统方法,折射率和复介电常数
注意这一部分最重要的内容:le modèle de Drude主要在TD中出现
基础知识
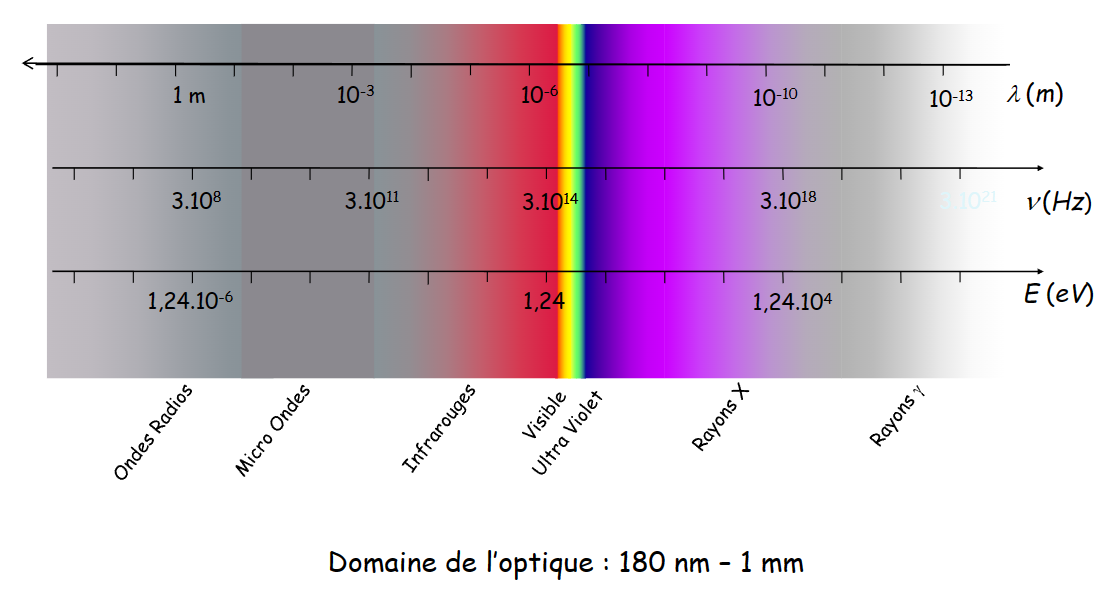
光的基础知识

原子的谐振子模型

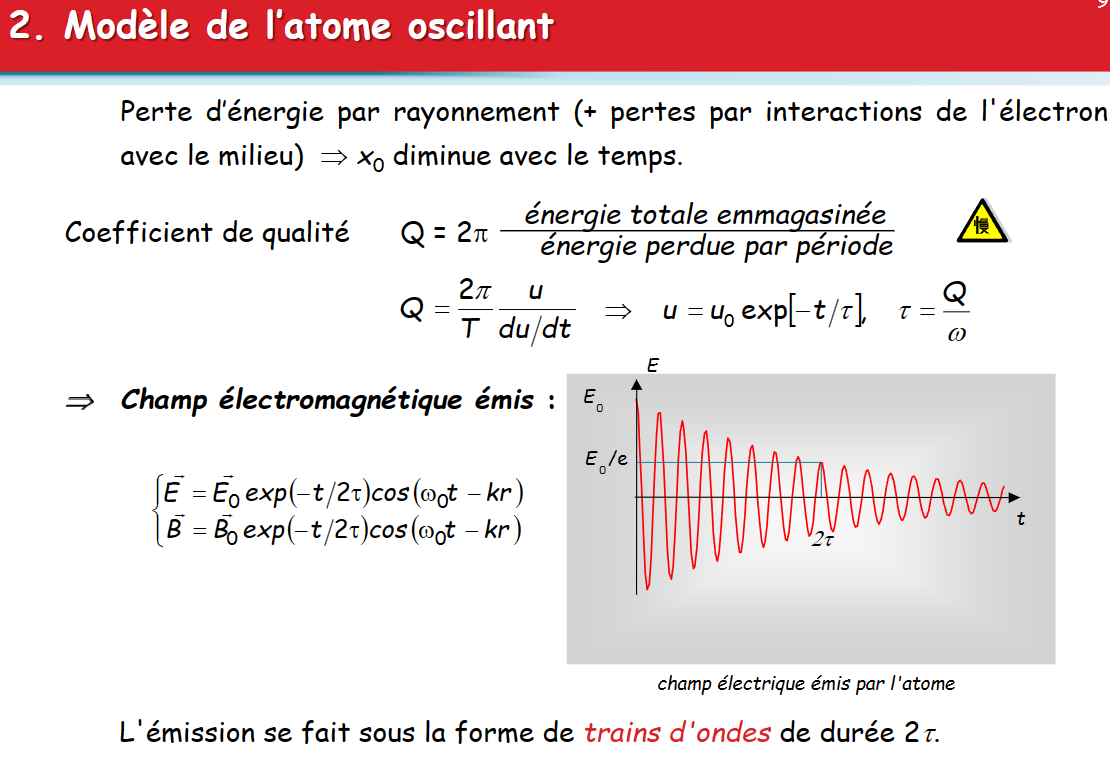
- 运动方程:$m_e\frac{d^2x}{dt^2} = -kx \quad avec \quad \omega_0 = \sqrt{\frac k {m_e}}$
- 运动方程的简谐解:$x = x_0cos\omega_0t$
- 偶极子:$p = -ex_ocos(\omega_0t)$
- 辐射电场:$\vec E = \frac 1{4\pi \varepsilon0}(-\frac{\omega_0^2sin(\theta)}{rc^2})p_0e^{-i(\omega t-kr)}\vec e{\theta}, \quad r \gg r_o$
- 辐射平均功率:$P_m = \frac 1{4\pi \varepsilon_0} \frac{\omega_0^4(ex_0)^2}{3c^3}$
光谱的归一化
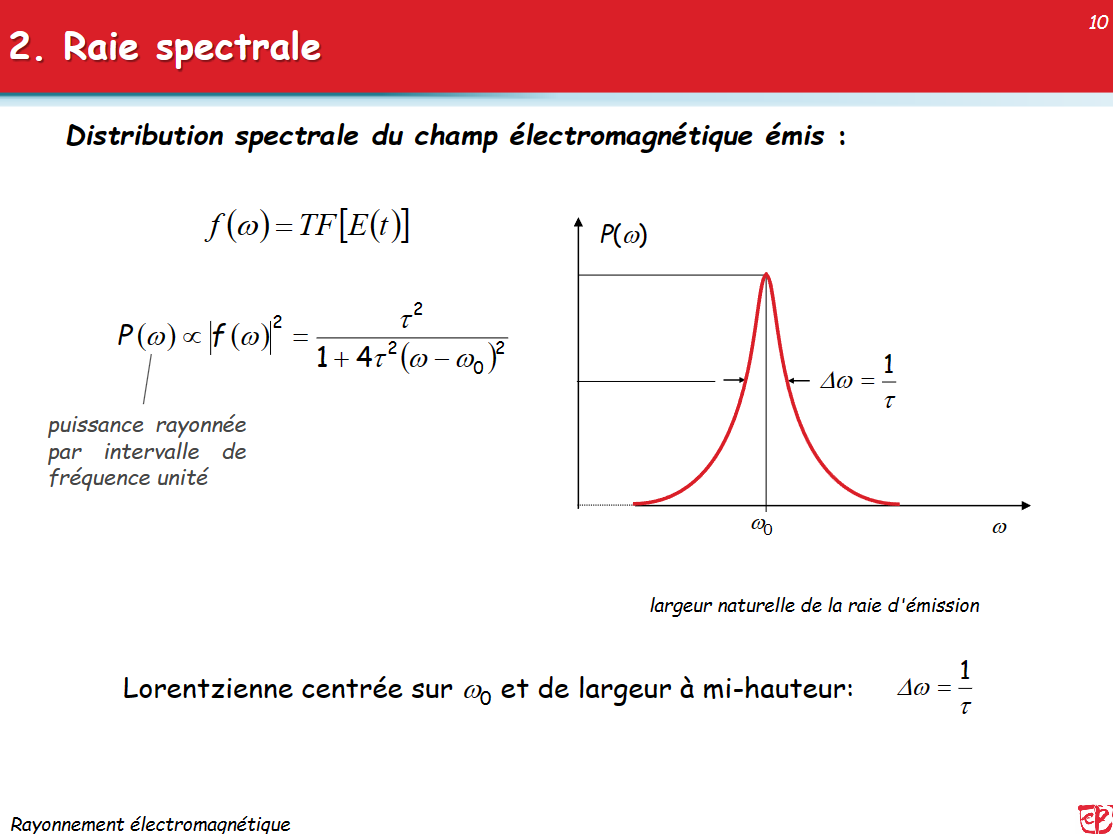

介质中的麦克斯韦方程

Résumé

光在物质中传播
偶极
构造方程

- 构造方程
- 极化率:$\alpha$
- $\varepsilon = 1+N\alpha=1+\chi$
单电子原子:阻尼谐振模型
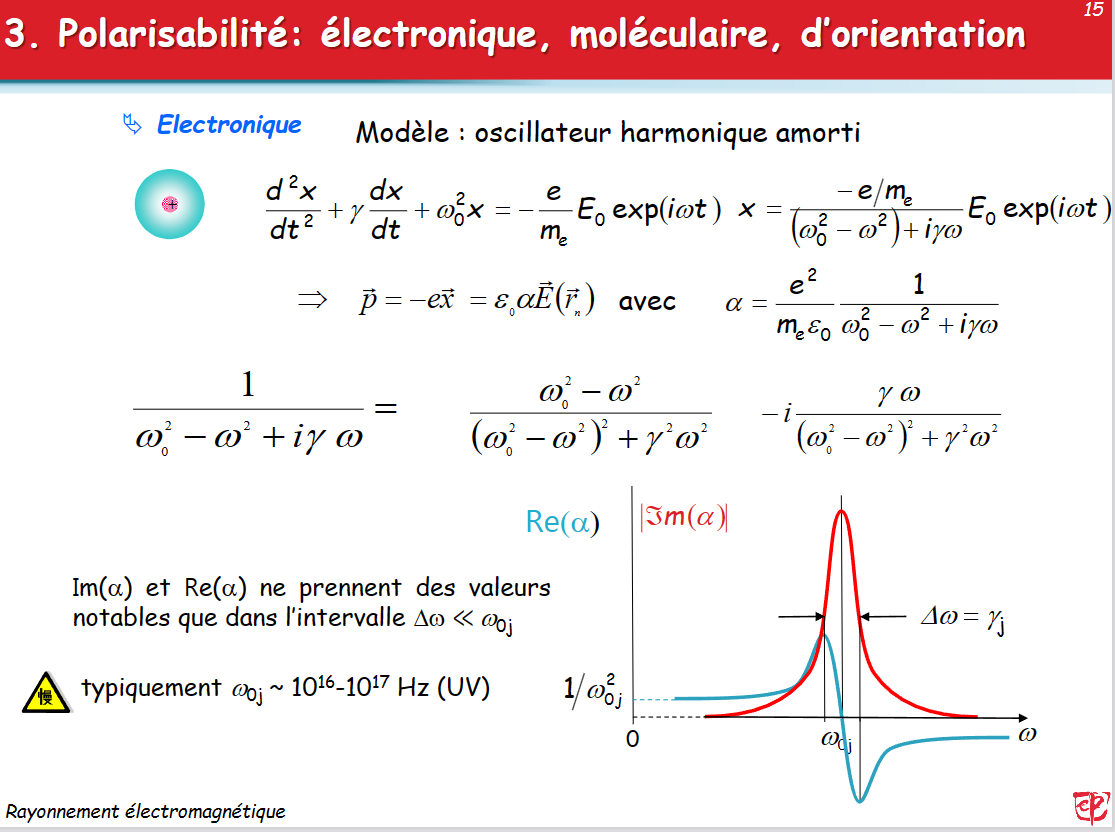
- 运动方程:
- 解得:$x = \frac{-e/m_e}{(\omega_0^2-\omega^2)+i\gamma\omega}E_0exp(i\omega t)$
- 偶极:$\vec p = -e \vec x = \varepsilon_0\alpha\vec E(\vec r_n)$
- 得到极化系数:
- 对于第$j$能级,$\omega_{0j}\thicksim10^{16}-10^{17}Hz(UV)$
多电子原子,带电原子/分子:叠加
假设对于某个能级,$fj$个电子有着相同的$\omega{0j}$和$\gamma_j$
- 叠加后的极化系数:
假设对于某个带电粒子,其电荷为qj,质量为m_j,有相应的$\omega{0j}$和$\gamma_j$
- 对于单个带电粒子:
- 叠加之后的极化系数(如果需要):
- 对于带电原子/分子,其$\omega_0j$在红外区域
- $\varepsilon = 1+N\alpha$
有向极化 d ’orientation
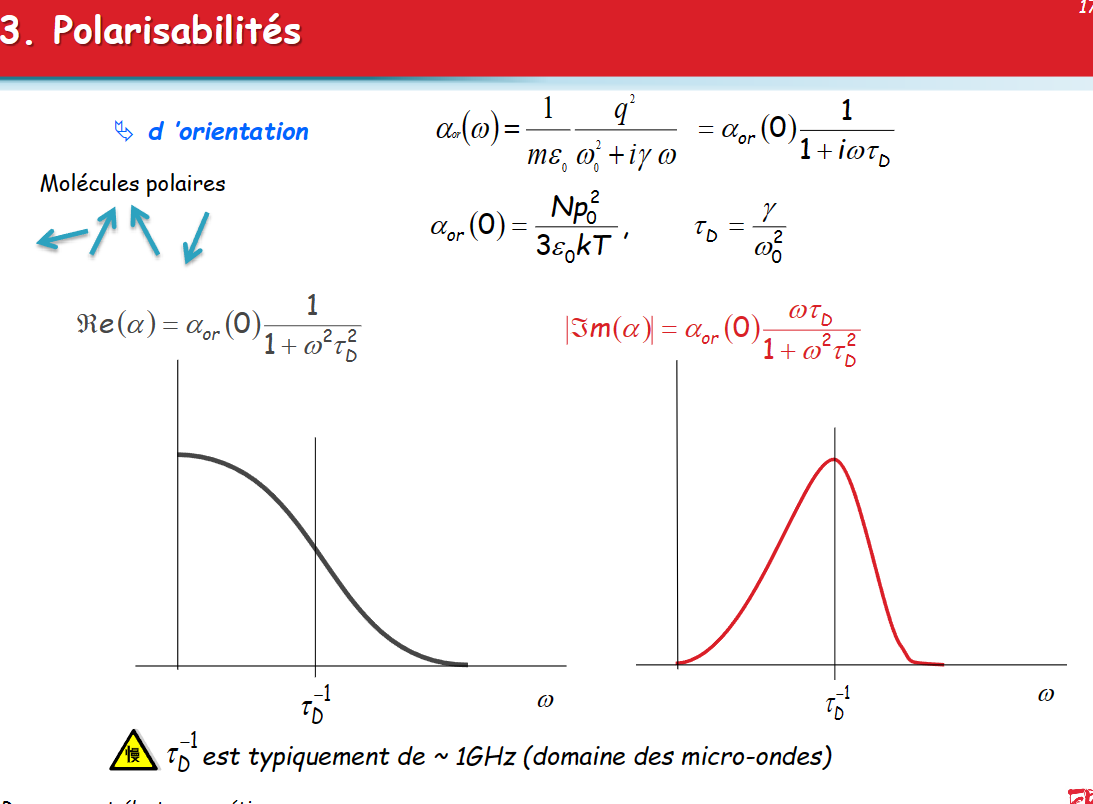

- 有向极化特征频率在微博范围,在微波炉中应用
介电函数 Fonction diélectrique & Résumé

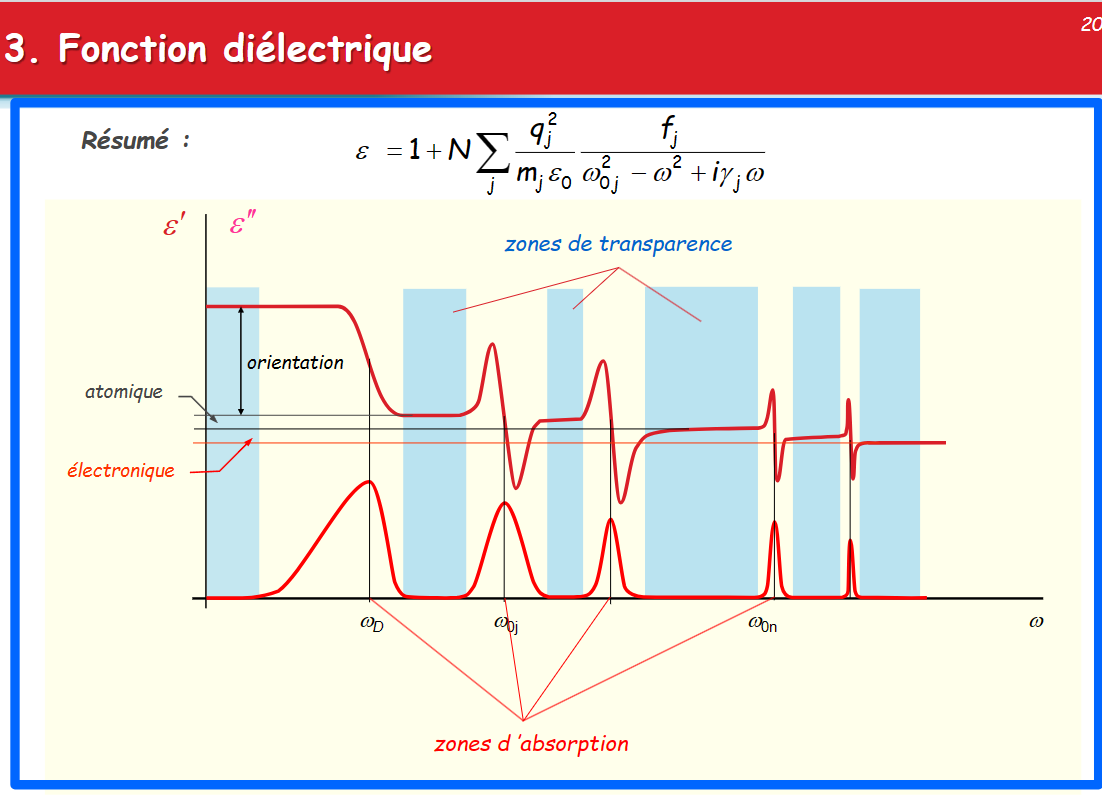
折射率和复介电常数
折射率和复介电常数之间的关系
从复介电常数到折射率和消光系数
在介质L.H.I.中传播 Milieux Linéaires Homogènes et Isotropes
$\vec \Delta \vec E - \varepsilon_0\varepsilon\mu_0\mu\frac{\partial ^2 \vec E}{\partial t^2}-\vec {grad} (div\vec E)-\mu_0\mu\frac{\partial \vec J}{\partial t} = 0$
宏观电中性,绝缘环境,简谐场
- 宏观电中性:$div\vec D = 0 \Rightarrow div \vec E = 0$
- 绝缘:$\vec J = 0 \Rightarrow \frac{\partial \vec J}{\partial t} = 0$
- 简谐场:$\vec E = \vec E_0exp(i\omega t-i\vec k\vec r)$
- 简化后的方程:$\vec \Delta \vec E - \vec k^2\vec E = 0$
- 色散关系:$\vec k^2 = \frac{\omega^2}{c^2}\varepsilon\mu$
宏观电中性,导体
- 导体:$\vec J = \sigma\vec E$
- 简化后的方程:$\vec \Delta\vec E+\frac{\omega^2}{c^2}\mu(\varepsilon-i\frac{\sigma}{\varepsilon_0\omega})\vec E = 0$
- 广义介电函数:$\widetilde{\varepsilon} = \varepsilon-i\frac \sigma {\varepsilon_0\omega}$
- 与偶极子的联系:
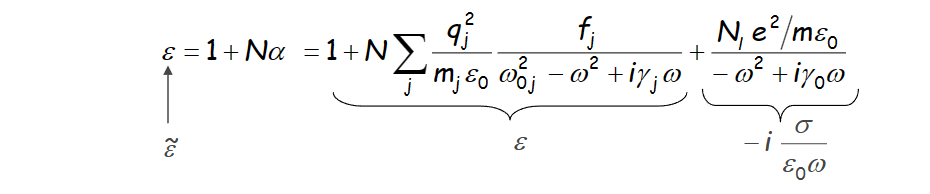
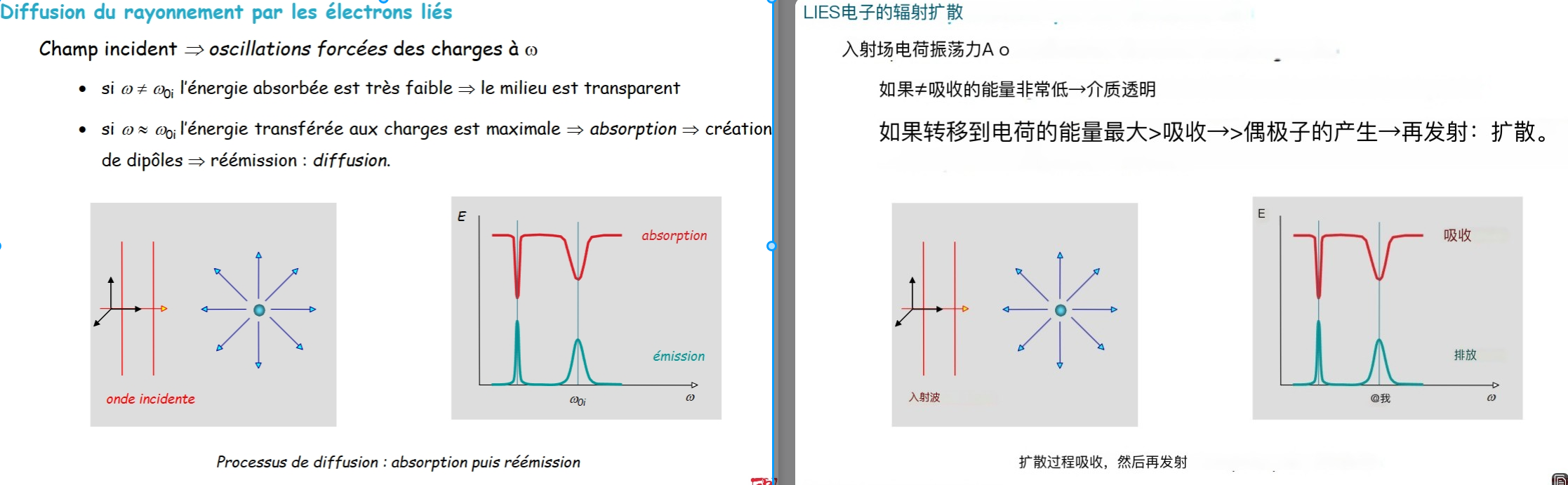
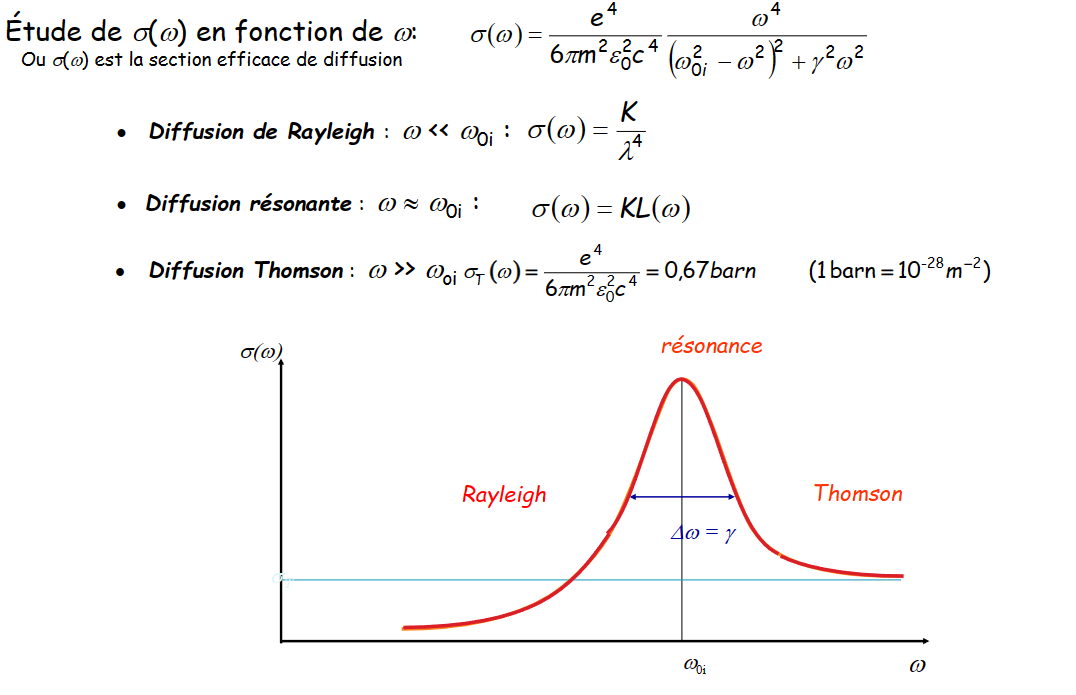
散射 Diffusion
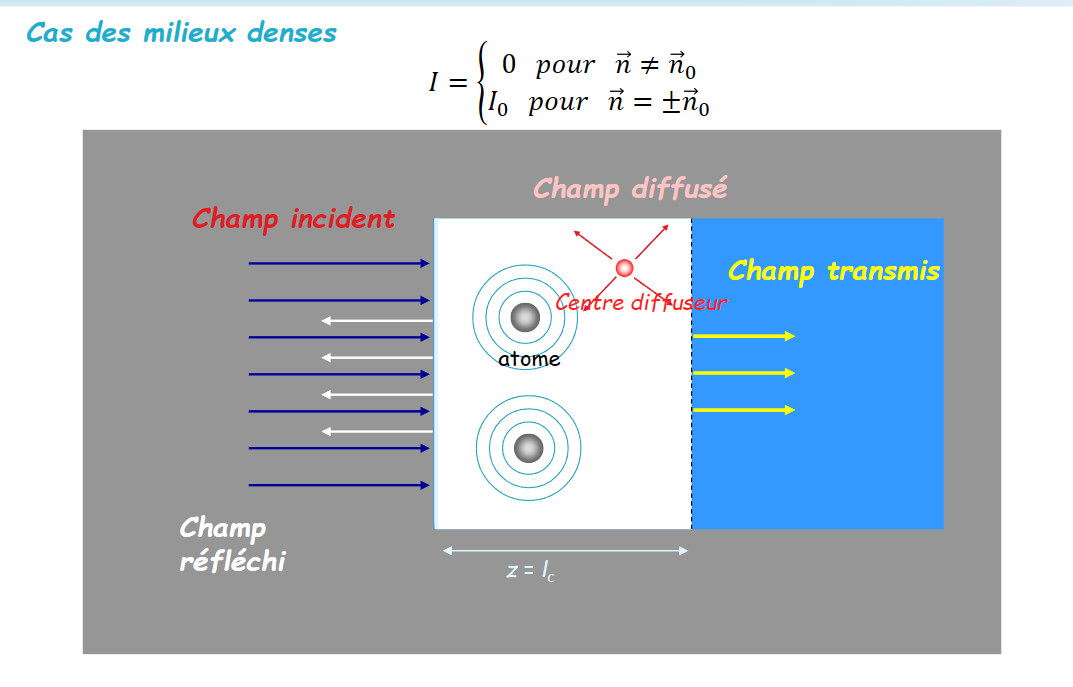
光学原理:折射和反射


Résumé

本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Raphael's Home!