Cours 3：光缆，共振腔

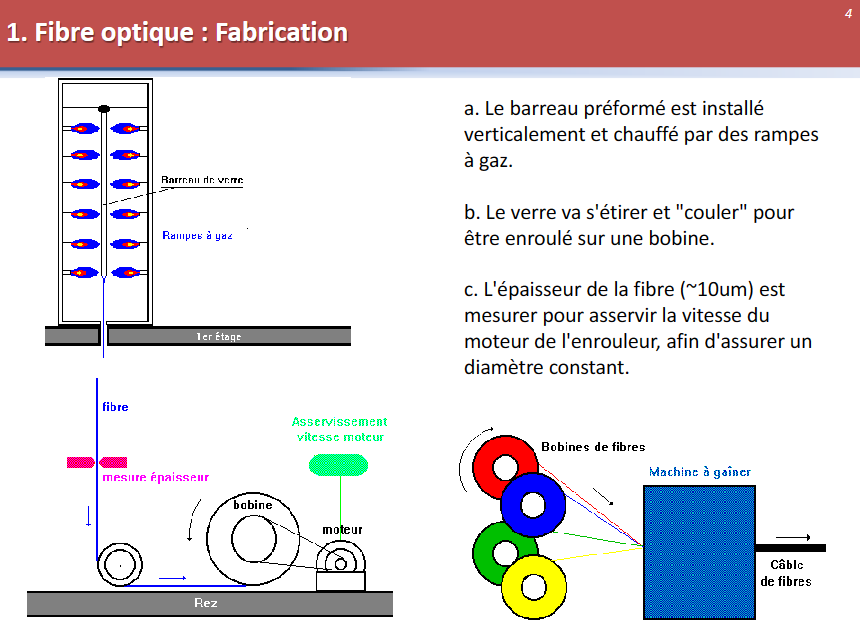
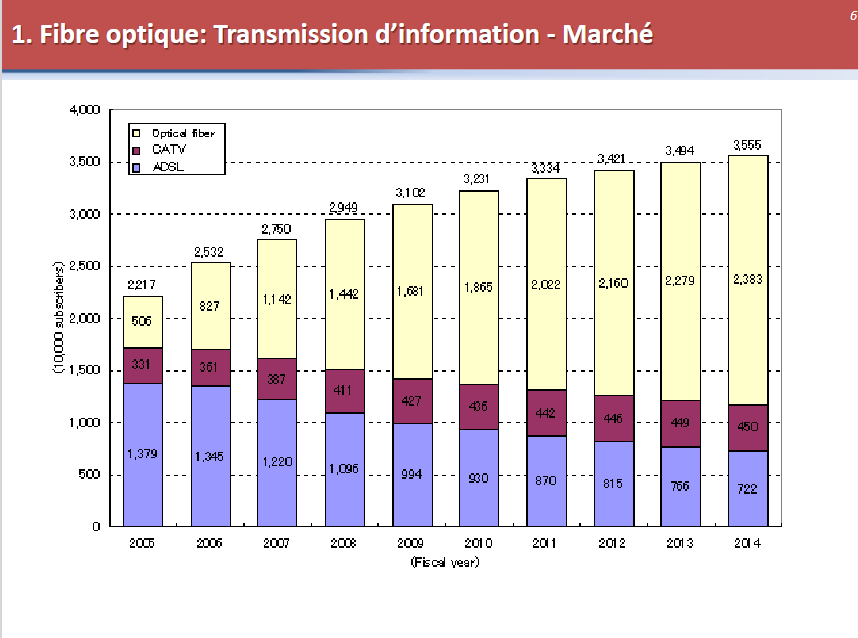
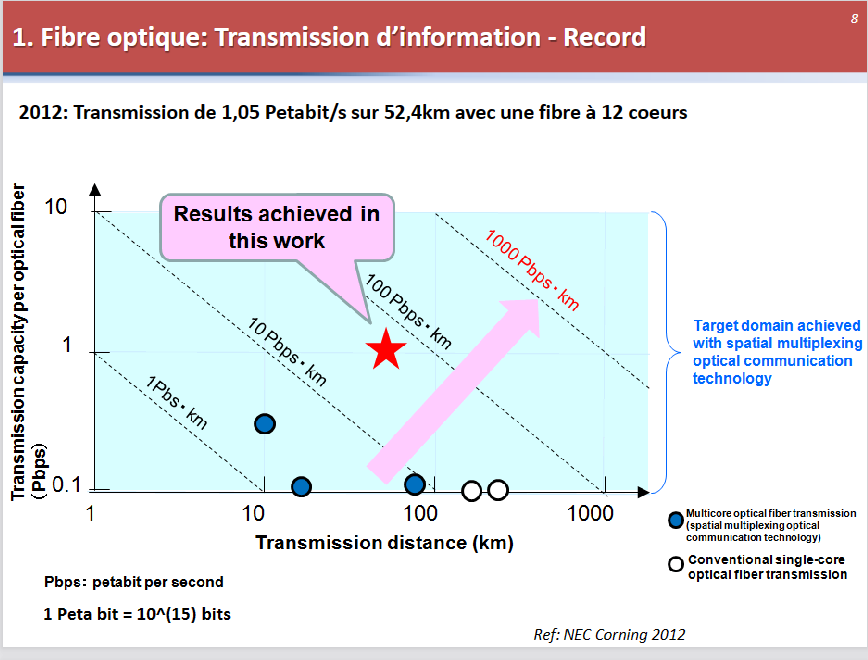
光缆的制造的应用

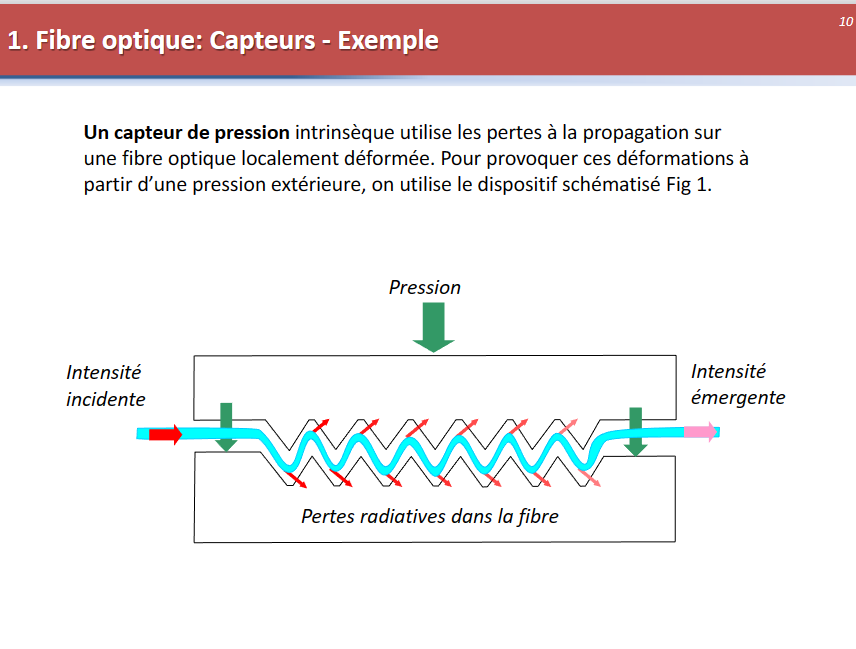
共振腔 Cavités résonantes

基本介绍

单维度共振腔 cavité Fabry-Pérot

电场强度

  • 方程：\(\frac{\partial^2 E_x}{\partial z^2}+k_z^2E_x = 0, E_x(0) = E_x(L) = 0\)
  • 解得：\(E_x(z) = aexp(ik_zz)+bexp(-ik_zz)\)
  • 代入初始条件：
    • \(E_x(0)=0\Rightarrow b = -a \Rightarrow E_x = -2iasink_z z\)
    • \(E_x(L) = 0\Rightarrow sink_zL =0\Rightarrow k_z = m\frac \pi L\)
  • 考虑时间因素，得到最终的电场强度公式：

\[ E_x(x,t) = E_{x0}sin(k_zZ)exp(i\omega t) \]

模式信息：波矢，频率，模态间隔，模数，模密度

  • 波矢：\(k_m = m\frac \pi L\)
  • 频率：\(\nu_m = m\frac c{2(n)L}\)
  • 模态间距：\(\Delta\nu_c = \frac c{2(n)L}\)
  • Nombre de mode：\(N(\nu) = \frac 1 {\Delta \nu_c} = \frac{2L}{c}(Hz)^{-1}\)
  • Densité de mode：\(M(\nu) = \frac{2N(\nu)}{L} = \frac 4c(Hz^{-1}m^{-1})\)，这里的2是考虑了\(x，y\)两个偏振方向

考虑反射带来的损失

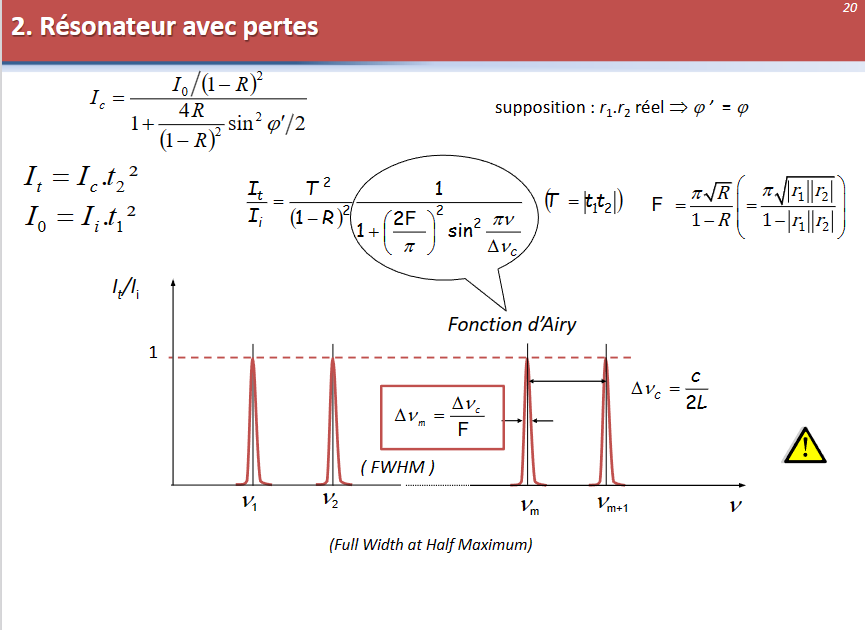
  • 上图易于理解，更加详细的解释可以参照第6课激光的相应部分或者TD的相应内容
  • \(T = |t_1t_2|\)
  • \(F = \frac{\pi \sqrt{R}}{1-R} = \frac{\pi\sqrt{|r_1||r_2|}}{1-|r_1||r_2|}\)
  • 由于反射带来的峰变宽的量：\(\Delta\nu_m = \frac {\Delta \nu_c}F\)

考虑其他因素带来的损失，以及两种假设

  • 在真实情况下还会有其他因素带来的损失：

\[ \frac{u(\nu,2L)}{u(\nu,0)} = R_1R_2e^{-2\alpha L} \]

  • 注意这里是能量关系，相位变化\(e^{ikz}\)不会考虑在其中
  • 假设所有的损失都发生在过程中toutes les pertes sont réparties à l’intérieur de la cavité：

\[ \frac{u(\nu,2L)}{u(\nu,0)} = R_1R_2e^{-2\alpha L} = e^{-2\alpha_eL}\quad avec \quad \alpha_e = \alpha-\frac 1{2L}ln(R_1R_2) \]

  • 假设所有损失都发生在镜子处toutes les pertes sont localisées sur les miroirs：

\[ \frac{u(\nu,2L)}{u(\nu,0)} = R_1R_2e^{-2\alpha L} = R_e^2\quad avec \quad R_e = \sqrt{R_1R_2}e^{-\alpha L} = e^{-\alpha_eL} \]

  • 在这种情况下，损失函数\(F=\frac{\pi \sqrt{R_e}}{1-R_e} = \frac{\pi e^{-\alpha_e L/2}}{1-e^{-\alpha_e L}}\)
  • 当 \(\alpha_eL\ll1, F\approx \frac \pi {\alpha_eL}\)

品质因子 Coefficient de qualité de la cavité，腔中光子寿命 durée de vie du photon，距离衰减系数\(\alpha_c\)

\(Q = \frac \nu {\Delta \nu_m} = 2\pi\frac{总能量}{每周期能量损失} = 2\pi\frac{u}{\frac{du}{dt}T} = \frac{m\Delta \nu_c}{\frac{\Delta \nu_c}{F}} = mF\)

  • 推得：

\[ \frac{du}{dt} = -\frac{\omega}{Q}u\Rightarrow u(\nu,t)exp(-t/\tau_c)\quad avec \quad \tau_c = Q/\omega \]

  • 引入的\(\tau_c\)是腔中光子的寿命
  • 将t替换为z：

\[ z = ct\Rightarrow u(\nu,z) = u(\nu,0)exp(-\frac{\omega}{cQ}z) = u(\nu,0)exp(-\alpha_cz) \]

三维共振腔

  • 色散关系：\(k^2 = \frac{\omega^2}{c^2} = \pi^2[\frac{m^2}{a^2}+\frac{n^2}{b^2}+\frac{q^2}{c^2}]\)
  • 模式数：\(N = \frac 13\frac{k^3}{\pi^2}d^3\)
  • 模式密度：\(M = \frac{8\pi\nu^2}{c^3}\)
  • 模式频率：\(\nu_{mnq}\approx\frac{qc}{2L}+(m^2+n^2)\frac{cL}{4qa^2}\)

其他共振腔

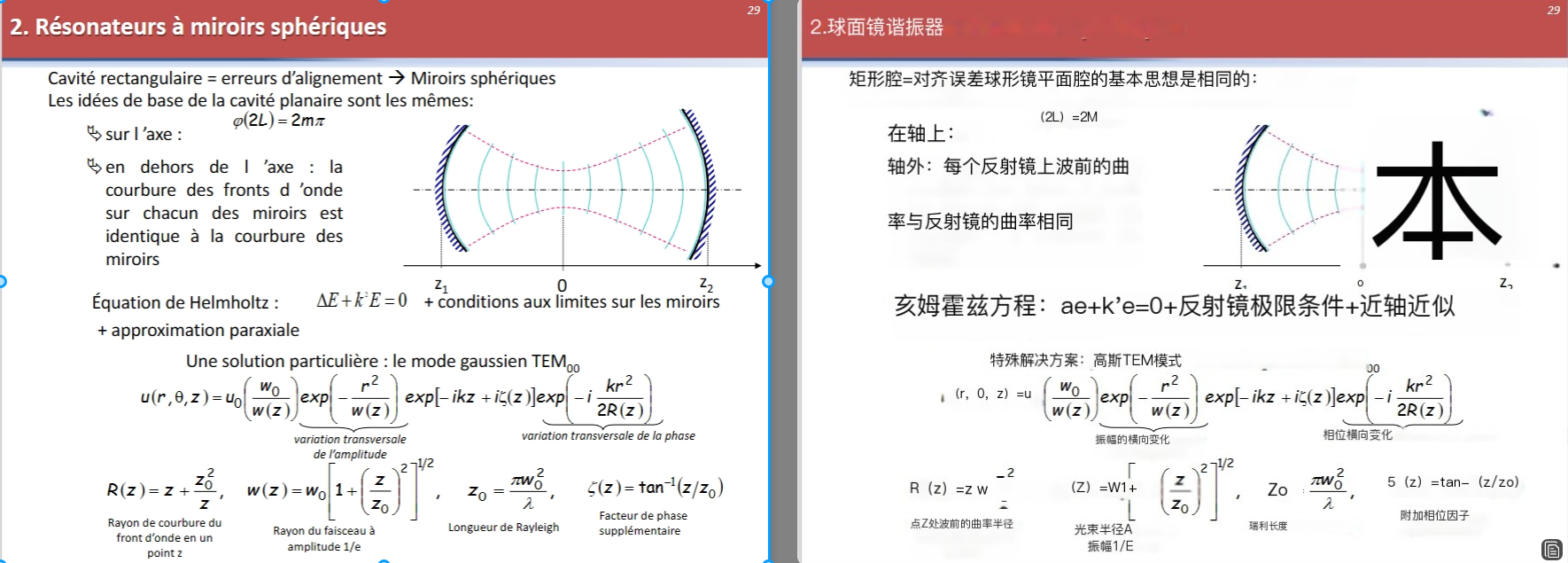
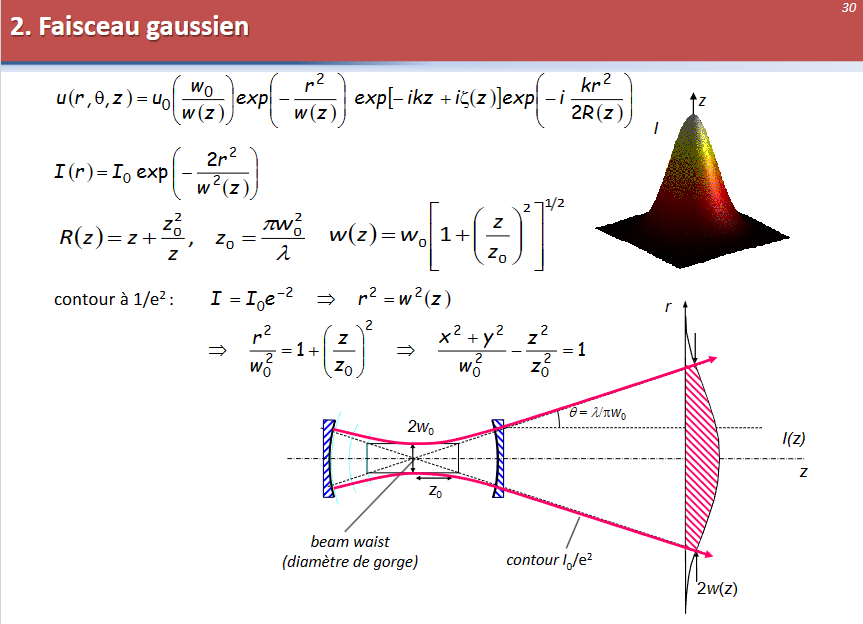
RÉSUMÉ