Cours 2 傅里叶光学,电磁学基础,波导
Cours 2 傅里叶光学,电磁学基础,波导
傅里叶光学
散射
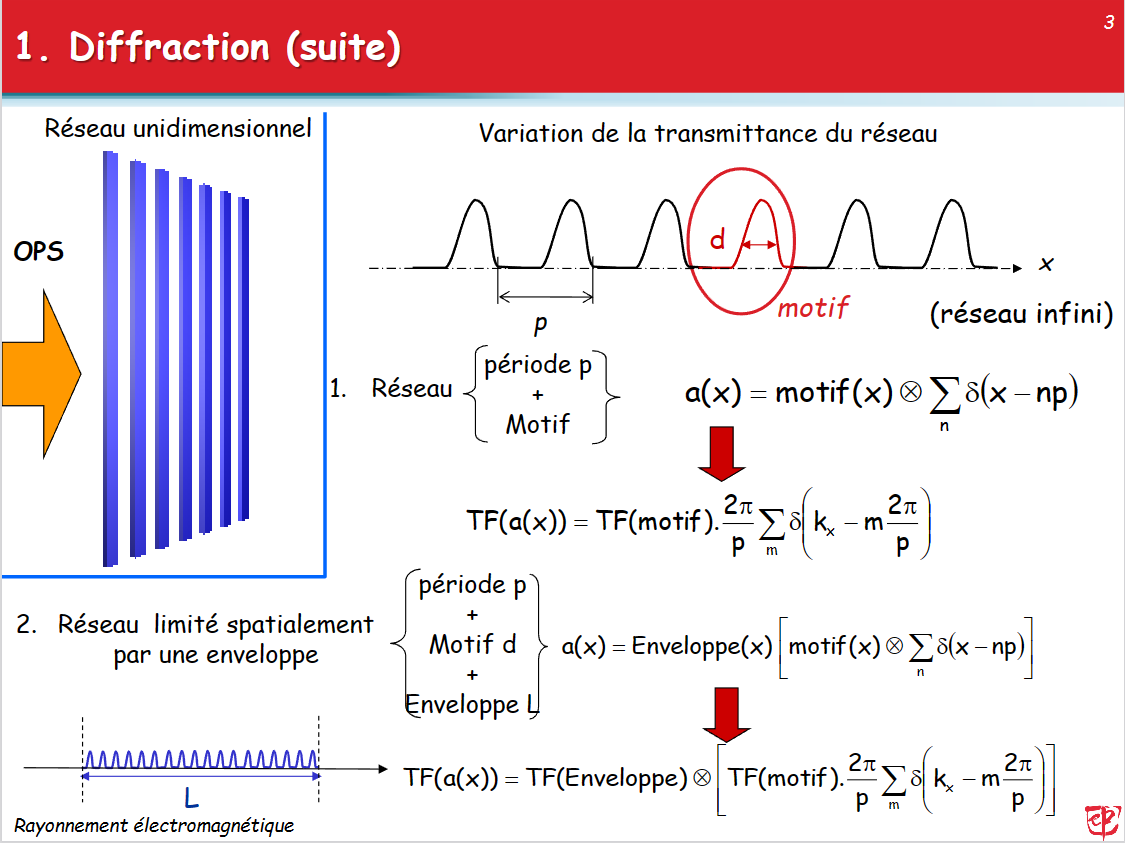
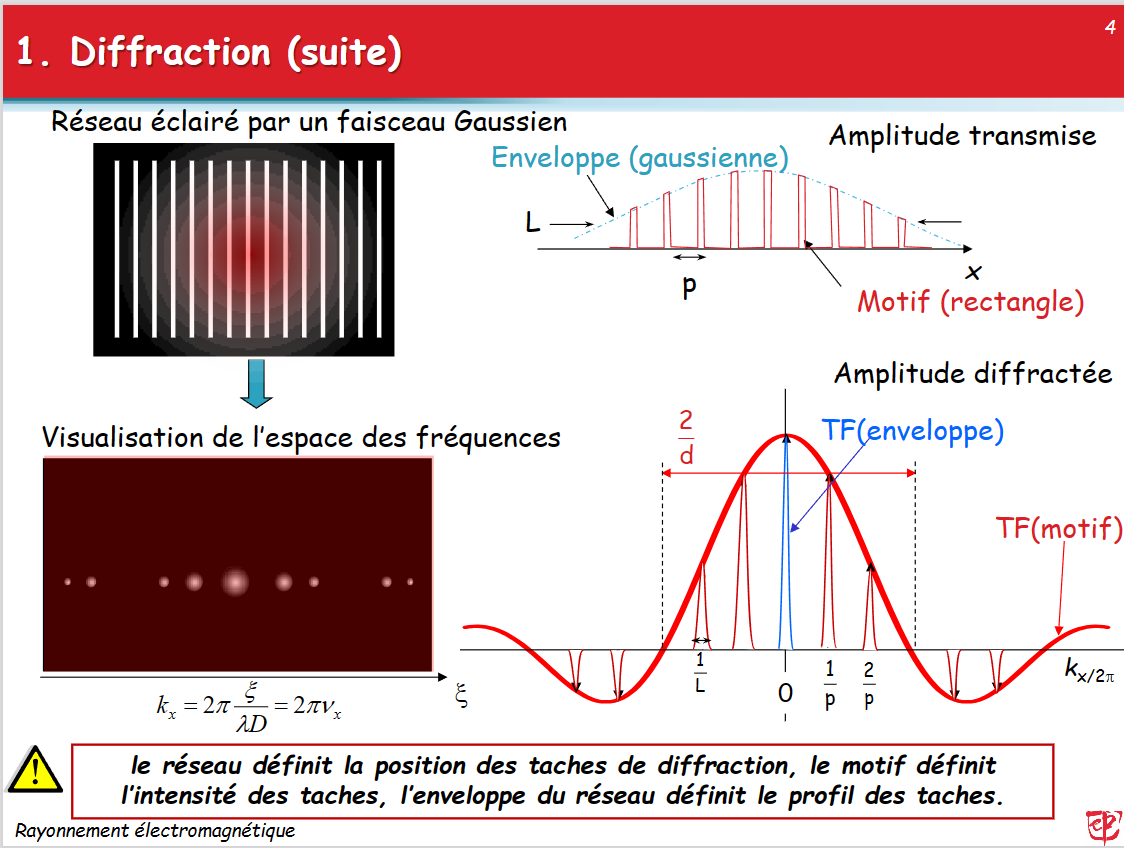
- 关于傅里叶变换到频率还是角频率:
\[ \frac{2\pi}{p}\sum\delta(k_x-m\frac{2\pi}{p}) = \frac{2\pi}{p}\sum\delta(2\pi \sigma_x-m\frac{2\pi}{p}) = \frac{2\pi}{|2\pi|p}\sum\delta( \sigma_x-m\frac{1}{p}) = \frac{1}{p}\sum\delta( \sigma_x-m\frac{1}{p}) \]
- 注意,傅里叶变换完之后的结果是\(K_x\)和\(K_y\),我们要将其转换为坐标\(\xi,\eta\)转换公式:
\[ K_x = k\frac {\xi} z = \frac {2\pi\xi} {\lambda z}\\K_y = k\frac \eta z = \frac {2\pi\eta} {\lambda z} \]
电磁学基础


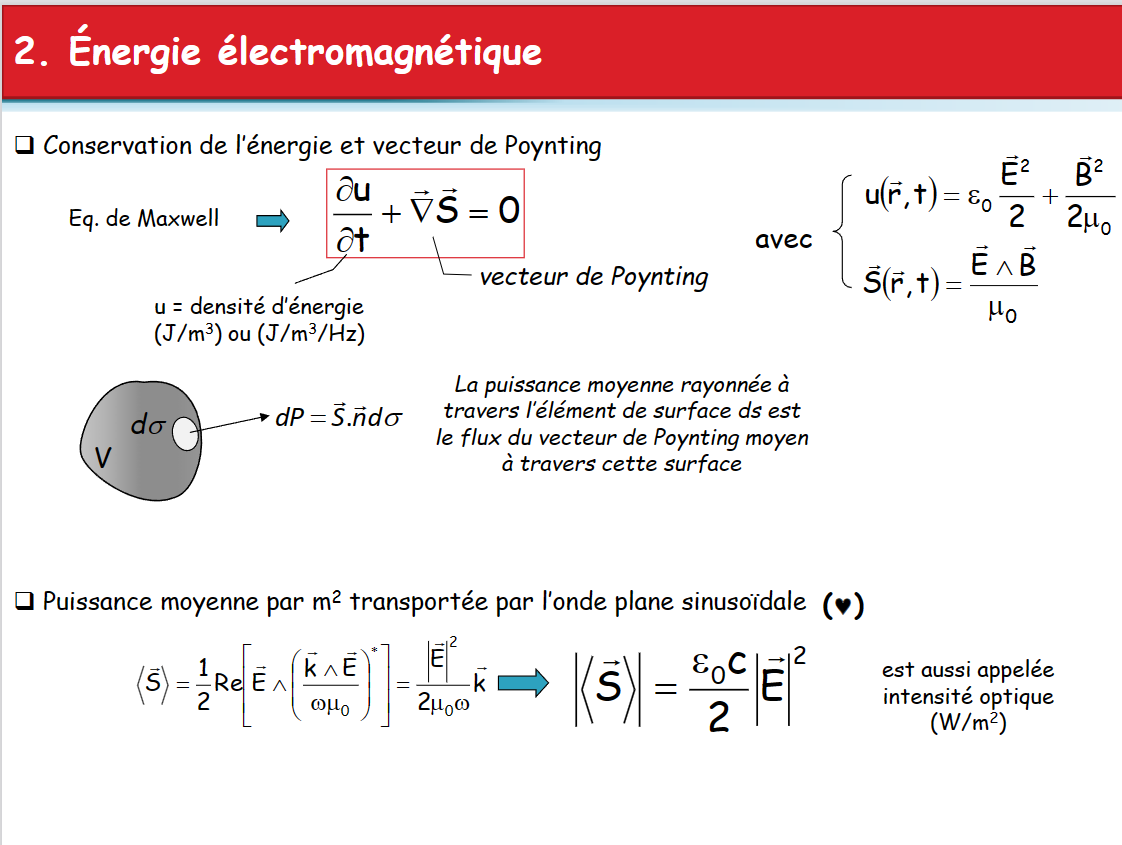





真空中
结构关系
- \(\vec B = \frac{\vec k \land \vec E}{\omega}\)
色散关系relation de dispersion
- \(k = \frac{\omega}{c}\)
能量关系
- \(\frac{du}{dt} + div(\vec S) = 0\)
- 能量:\(u = \epsilon_0\frac{\vec E^2}{2}+\frac{\vec B}{2\mu_0}\)
- Poynting矢量:\(\vec S = \frac{\vec E \land \vec B}{\mu_0}\)
介质中
色散关系
- \(\vec k^2 = \frac{\omega^2}{c^2}\widetilde\epsilon\mu \Rightarrow k = \frac \omega c \widetilde n\)
吸收和色散
- \(\vec E = \vec E_0 exp(-\frac{\omega \kappa}{c})exp(i\omega(t-\frac{n}{c}z)), n = Re(\widetilde n), \kappa = Im(\widetilde n)\)
穿透深度 Profondeur de pénétration
- \(\delta = \frac c {\omega\kappa} = \frac{\lambda}{2\pi\kappa}\)
衰减效率 Coefficient d’atténuation
- \(\alpha = 2\frac{\omega\kappa}c = \frac{4\pi\kappa}\lambda\)
波导
导向模式
模态
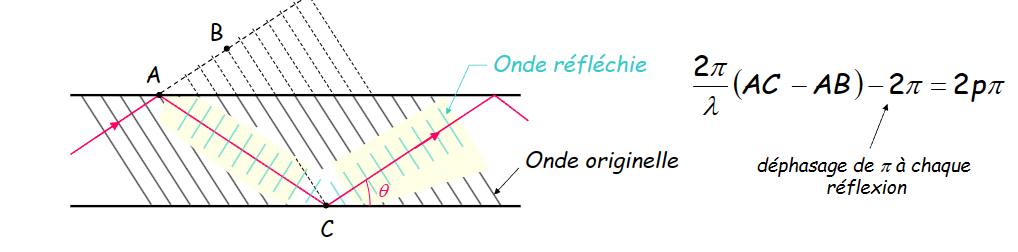
- 有\(AC-AB = 2dsin(\theta)\Rightarrow sin(\theta_m) = m\frac{\lambda}{2d}\)
- m被称为模态modes
- 第m模态的频率:\(\nu_m = m\frac{c}{2d}\)
纵向守恒
对于同一模态,波矢的y方向分量为常数:\(k_y = k_y(m)\)
\[ k_{ym} = m\frac \pi d \]
\[ \beta_m^2 = k^2-\frac{m^2\pi^2}{d^2} \Leftrightarrow k^2 = \beta^2+k_y^{2} \]
模态数量
设M为最大可允许的模态数量,根据\(sin(\theta_m) = m\frac{\lambda}{2d}\),有:
\[ M = E(\frac{2d}{\lambda}) = E(\nu\frac{2d}{c}) \]
- \(\lambda\)的最大值(\(M= 0\))longueur d ’onde de coupure du guide:\(\lambda_{max} = 2d\)
- \(\nu\)的最小值fréquence de coupure:\(\nu_{min} = \Delta\nu = \frac c{2d}\)
- 单模态条件: \(d\le\lambda\le2d\)
波导横向场分布




色散关系
- \(\beta^2_{m} = k^2-\frac{m^2\pi^2}{d^2} = \frac{\omega^2}{c^2}-\frac{m^2\pi^2}{d^2}\)
群速度
- \(v_{gm} = \frac{d\omega}{d\beta_m} = c^2\frac {\beta_m} \omega = \frac{c^2k}{\omega}cos\theta_m = c\cdot\cos\theta_m\)
二维波导

模态数量
\[ M\thickapprox2\times\frac{\frac \pi 4(nk_0)^2}{\frac{\pi}{d}^2} = \frac \pi 2(\frac{2d}{\lambda})^2 \]
Résumé

本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Raphael's Home!