Cours 1 导论，傅里叶变换，群速度和相速度，波包，变形

第一课的原始笔记是手写笔记，在勤经苦舟笔记本6中。

导论

不同种类的波

• 平面波：\(\varphi（\vec{r},t） = \varphi_0exp(i(\omega t-\vec k \vec r))\)
• 球面波：\(\varphi（\vec{r},t） = \frac{\varphi_0}rexp(i(\omega t-\vec k \vec r))\)
• 驻波：\(\varphi（\vec{r},t） = \varphi_0cos(\omega t)cos(\vec k\vec r)\)

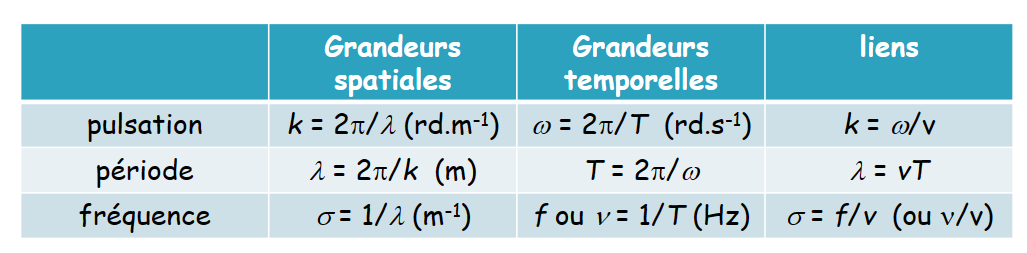
电磁波参数关系

傅里叶变换

常用函数傅里叶变换

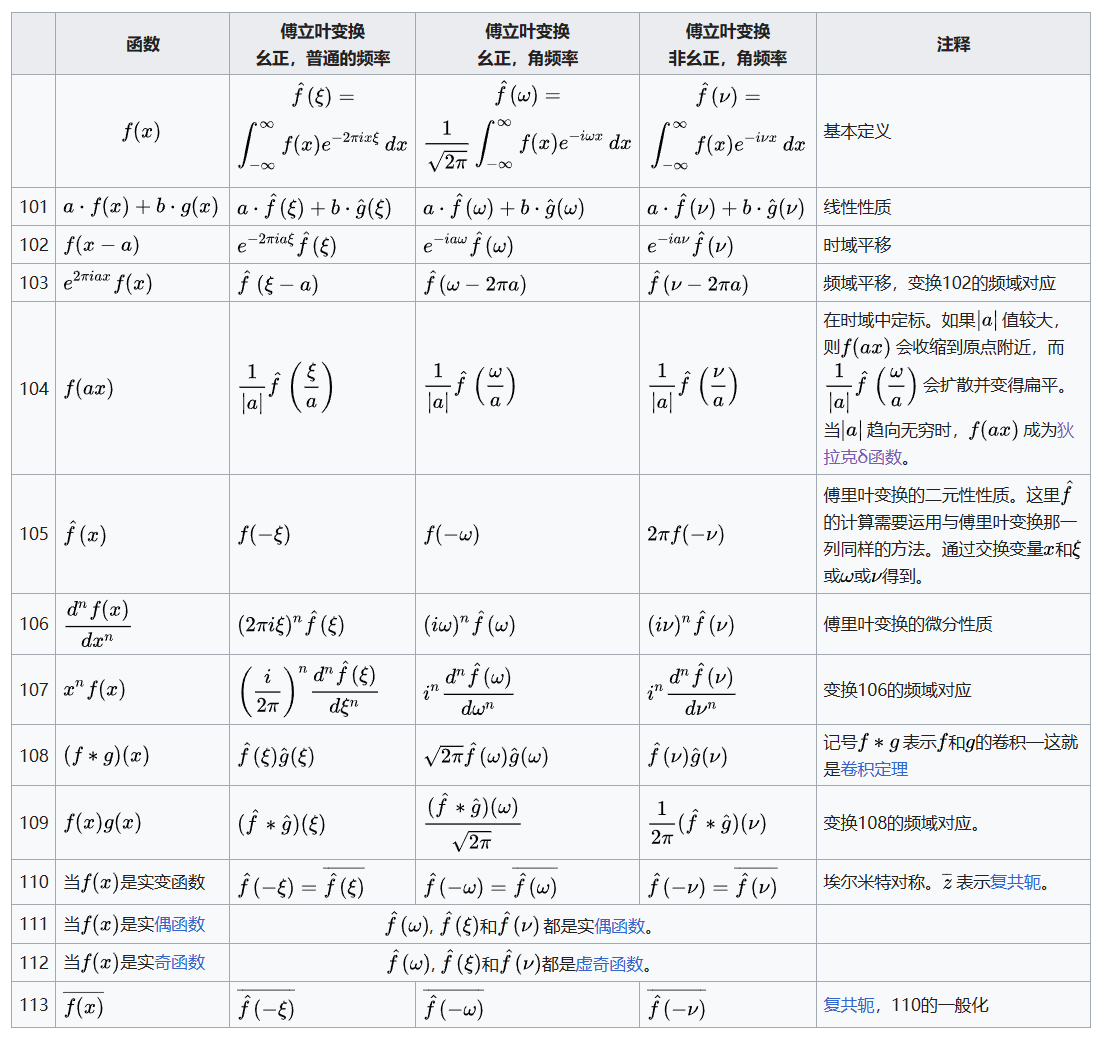
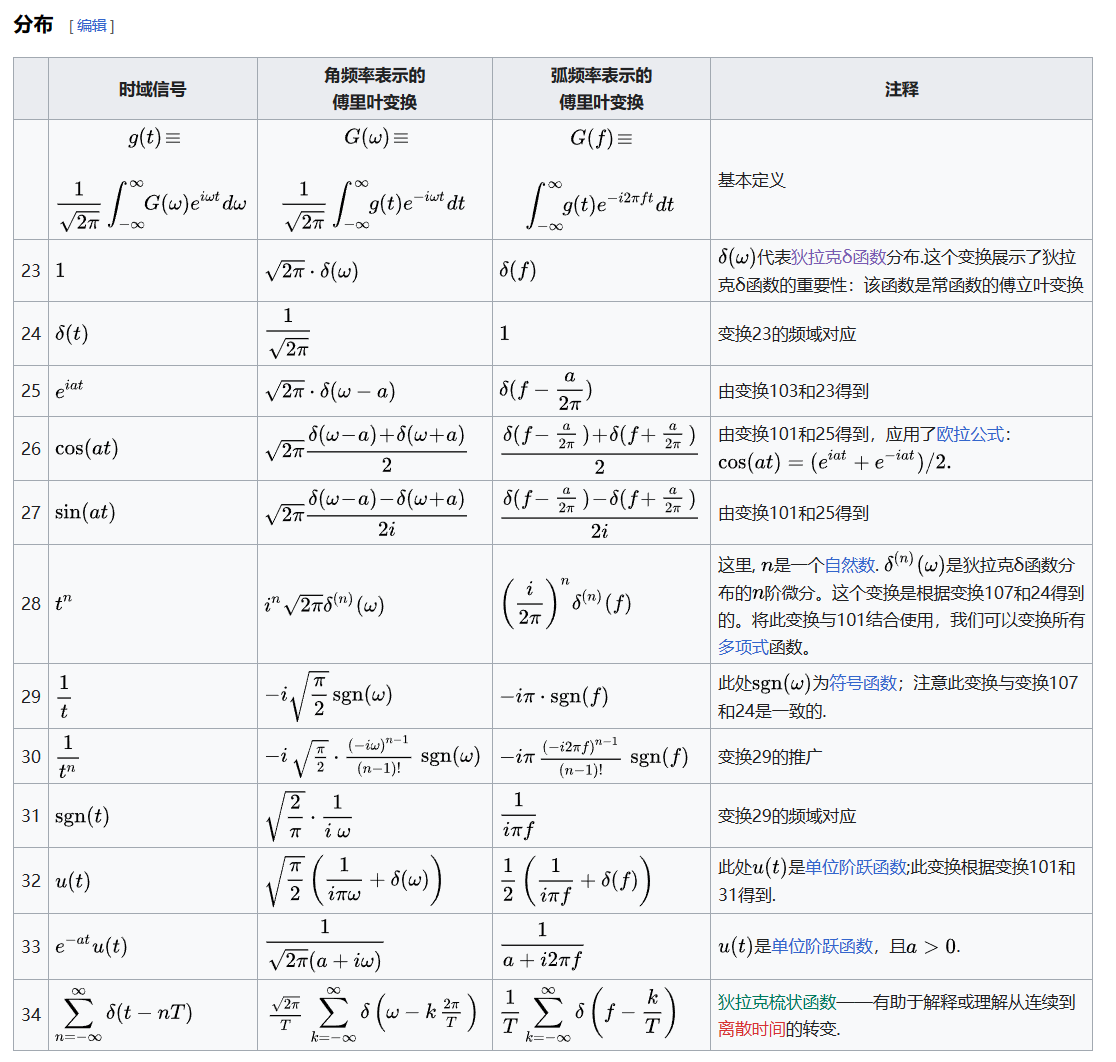
Spectre de fréquence 频谱

• \(|A(\omega)|^2 = 4|\widehat f (\omega)|^2_{\omega>0}\)

Entre largeurs

• 函数在\(x\pm\Delta x\)时取到0

Résumé:

波包 paquet d’onde

群速度和相速度

对于波\(\varphi(x,t) = \varphi_0exp(i(\omega t-kx))\)，有\(\varphi(x,t) = TF^{-1}[\widehat \phi_1(k)exp(i\omega t)]\)

将\(\omega\)对k展开：\(\omega = \omega_0+(\frac{d\omega}{dk})_{k_0}(k-k_0)+\eta\)

代入：

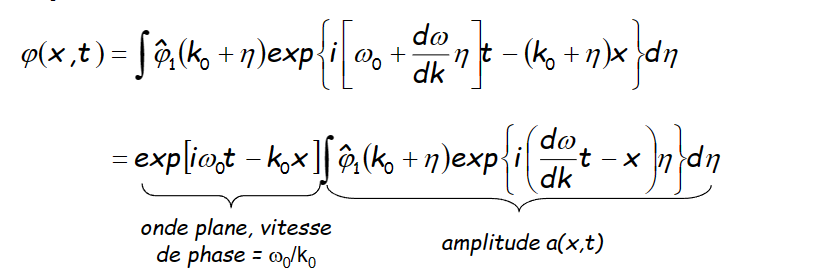
• 相速度[正弦波的传递速度]：\(v_\varphi = \frac{\omega_0}{k_0}\)
• 群速度[包络线的传递速度]：\(v_g = \frac{d\omega}{dk}\)
• 群速度不等于相速度时，会发生色散

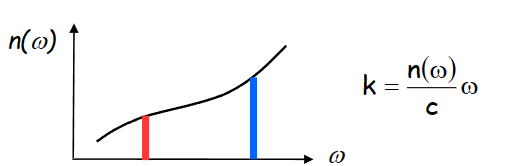
光学指数

• 光学指数：\(N_g= n+\omega\frac{dn}{d\omega}\)，其中，n代表折射率
• 此时有群速度：\(V_g= \frac{d\omega}{dk} = \frac{c}{n+\omega \frac{dn}{d\omega}} = \frac{c}{N_g}\)

变形

• 一般来说，一个波包的传递时间：\(t = \frac{L}{c}\)
• 但在介质中，传递事件发生变化：\(t = L\frac{N_g}{c}\)，此时到达时间会受到波长影响
• 对于波长展宽为\(\Delta\lambda\)的波，时间上的展宽\(\Delta \tau = \frac{dt}{d\lambda}\Delta \lambda = \frac{L}{c}|\frac{dN_g}{d\lambda}\Delta\lambda|\)
• 最终得到时间上展宽与空间上展宽的关系：

\[ \Delta \tau = \frac{L}{c}|\frac{d^2n}{d\lambda^2}|_{\lambda_0}\Delta\lambda \]