Atom & Atoms
Atom,Atoms
在目标研究的程序中,主要使用了这两个库
ase库中的Atom和Atoms是用于处理分子和结构的重要工具。Atom对象用于表示单个原子,它包含原子的元素类型、位置、速度等信息。Atoms对象是一个用于存储和操纵多个Atom对象的容器,它可以用来表示分子、晶体、表面等多种结构。除了原子的信息,Atoms对象还可以存储诸如晶格参数、原子间距、键长等结构信息。
Atom类
类Atom非常简单,基本只包含原子的非常基础的信息
初始化
12***class* ase.atom.Atom(*symbol='X'*, *position=(0, 0, 0)*, *tag=None*, *momentum=None*, *mass=None*, *magmom=None*, *charge=None*, *atoms=None*, *index=None*)**
symbol:分子式,可以使用化学符号’Si’或者相应的原子序号14来表示
position:三维坐标,单位为Å
tag:特殊用途标签
momentu ...
文件读写_ase_io
文件读写 ase.io
ase.io是一个用于处理文件读写的库。它提供了一系列方便的接口,可以帮助我们在编程时处理文件的读取、写入、更新等操作。使用ase.io,我们可以更方便地在各种环境下处理文件,极大地提高了开发效率。
ase.io.read
1234567**ase.io.read(*filename: [Union](https://docs.python.org/3.10/library/typing.html#typing.Union)[[str](https://docs.python.org/3.10/library/stdtypes.html#str), [PurePath](https://docs.python.org/3.10/library/pathlib.html#pathlib.PurePath), [IO](https://docs.python.org/3.10/library/typing.html#typing.IO)]*, *index: [Any](https://docs.python.org/3.10/library/ ...
DCGAN
DCGAN
Created: November 22, 2023 3:27 PM Class: 第七学期 Type: Quick Study
Reviewed: No Status: Not started
本文参考pyTorch的相应教程快速实践生成式对抗神经网络
DCGAN
Tutorial — PyTorch Tutorials 2.1.1+cu121 documentation
尝试实现的代码可以在以下链接找到,实际上与原文提供的代码基本完全相同:
GitHub -
RaphaelHyaan/GAN_etude: 学习使用GAN网络
本文很多内容是对此文章的拙略翻译
简介
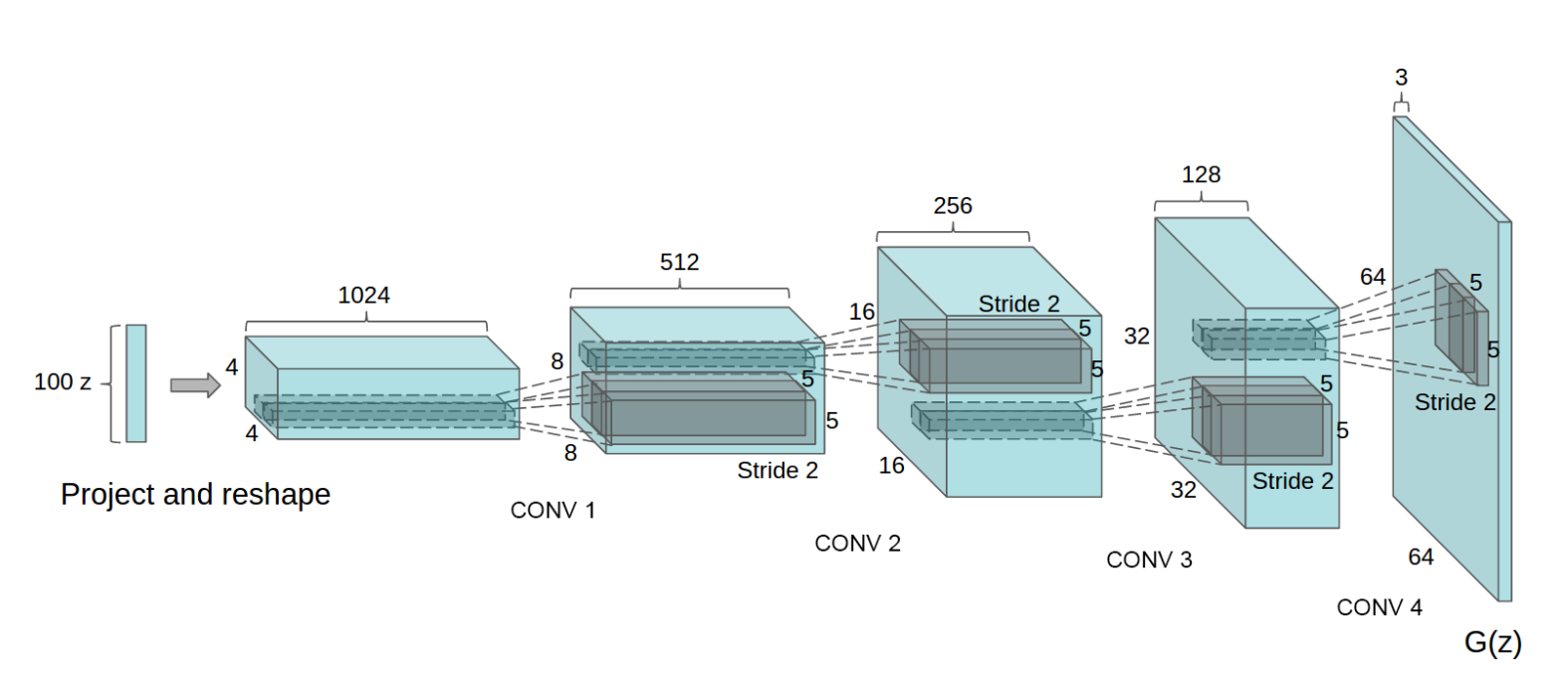
本教程将通过一个例子介绍DCGANs。我们将训练一个生成对抗网络(GAN)来生成新的名人,前提是向它展示了许多真实名人的照片。这里的大部分代码来自于pytorch/examples中的DCGAN实现,本文将详细解释实现,并阐明这个模型如何以及为什么工作。但是,不用担心,无需事先了解GANs,但是初学者可能需要花一些时间来推理实际上在底层发生了什么。另外,为了节省时间,最好 ...
电磁辐射波课程总览
已删除,仅保留此页以记录此笔记曾存在,以方便未来查找
本笔记更多为面向最终的开卷考试,故并不全面,包含大量老师原ppt的内容。TD内容尚可一看,但课程内容仅作参考。
Cours1_导论,傅里叶变换,群速度和相速度,波包,变形
Cours2_傅里叶光学,电磁学基础,波导
Cours3_光缆,共振腔
Cours4_射线-物质相互作用:传统方法,折射率和复介电常数
Cours5_光与物质相互作用的量子描述和半经典描述
Cours6_激光
Cours7_激光器
TD_1:
Poynting矢量,电场磁场结构关系,有效值之间的转化,偏振,波包'
TD_2:光栅,傅里叶光学'
TD_3:模式频率,模式频率间隔,有折射率导致的能量衰减,高斯光束'
TD_4:Drude模型,电导率,电流,复介电常数,折射率和消光系数'
TD_5:电解质中的Drude模型,数值近似,脉宽,群速度,光缆'
TD_6:爱因斯坦光电效应,双能级模型'
TD_7:四能级系统,粒子数反转'
机器人课程报告
机器人课程报告
背景介绍
在本次报告中可以被介绍一种用于武器的炮塔装置的建模。
机械臂在武器中应用较广,主要用于提高武器的稳定性和精准度。例如,在炮塔装置中,机械臂可以帮助精准地瞄准目标,并保持炮塔在移动过程中的稳定。此外,机械臂还可以用于自动装弹,提高射击效率。
对于用于射击的机械臂,例如教材中提及的有人操作的机械装置,其主要作用是快速辅助瞄准。本报告参考描述了一种基于地面的用于射击的模型。这种模型可以对一个确定的方向提供不错的打击能力。且配合汽车的移动或者类似于雷达车那样的平面转动方法,可以转换打击的方向。另外,这个模型具有不错的扩展性,现在的模型是一个近似串联的模型,而在实际应用时,可以通过增加机械臂数量的方式提供更强力的打击。
在本报告中,会对这种模型应用Denavit-Hartenberg的描述方法进一步简化,并分析其移动性,运动学,反运动学,和动力学。
模型建立
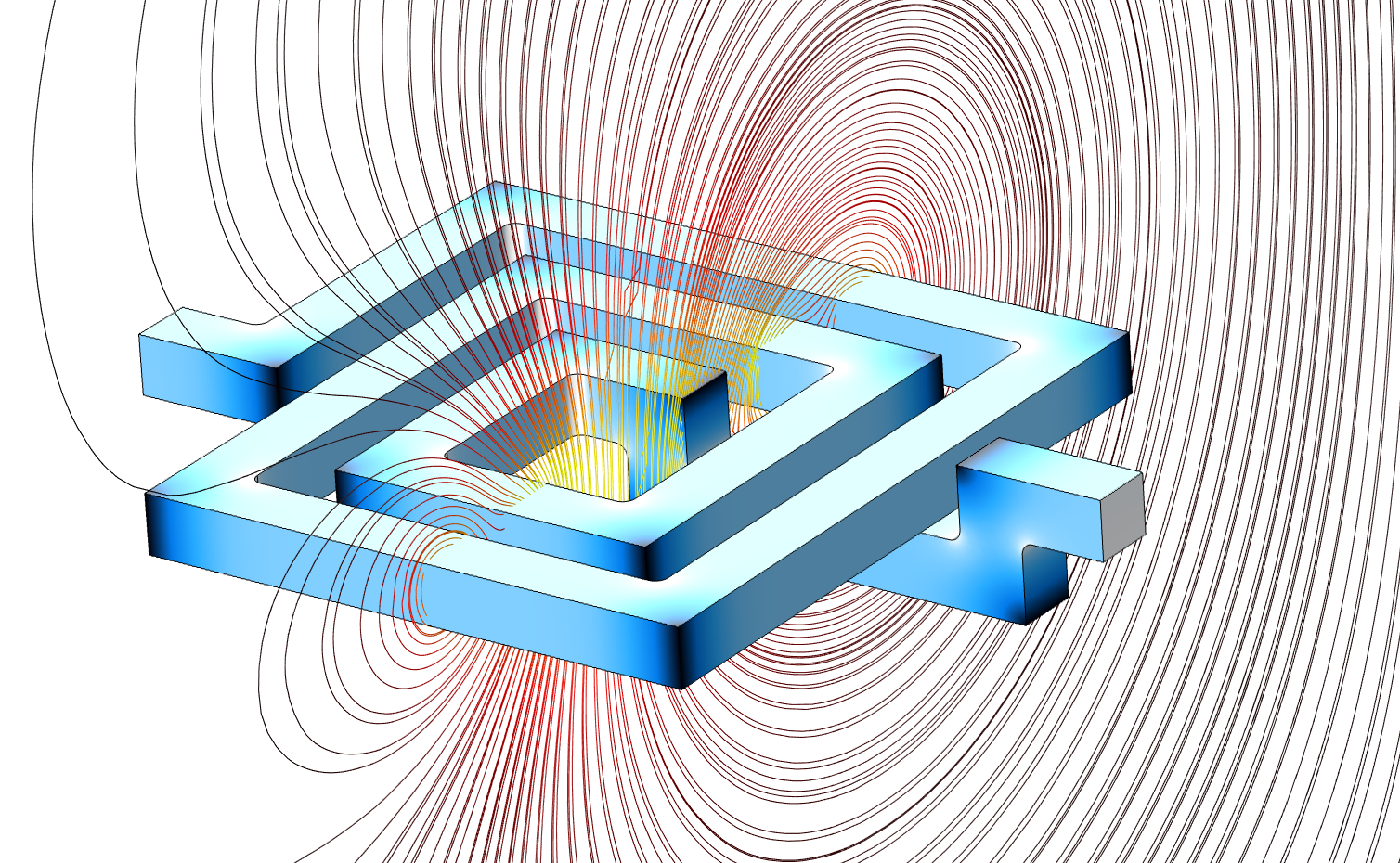
这篇报告中介绍的模型如下图所示,它具有6个自由度。在这6个自由度中,其中的4个自由度有转动副提供。其中,三个转动副的轴在同一平面,y轴(或x轴,在不同的计算中可能会有不同地约定方式)始终穿过这 ...
RDM Chapitre 4 能量方法 Méthodes Energétiques
RDM Chapitre 4
能量方法 Méthodes Energétiques
CSA,CCA,Travail
运动学上可允许的位移场和静力学上可允许的内力场
Champ de déplacement cinématiquement admissible &
Champ d’effort intérieur statiquement admissible
“Champ de déplacement cinématiquement
admissible”指的是在物理学,特别是可变形介质力学中,需要找到的一种位移场。这个位移场必须满足一些特定的边界条件,并且具有一定的规则性。这些条件定义了“cinématiquement
admissible”的位移场的空间,这个空间包含了所有满足边界条件的足够规则的位移场。记为:
\[
[\tilde{\mathrm{U}}]
\]
同样,“Champ d’effort intérieur statiquement
admissible”指的是在物理学,特别是连续介质力学中,需要找到的一种内部应力 ...
RDM Chapitre 3 变形,本构关系 Déformation, loi de comportement
RDM
Chapitre 3 变形,本构关系 Déformation, loi de comportement
位移和形变
位移螺旋 Torseur de
déplacement
对于等投影场:\(\overrightarrow{\mathrm{V}}_{\mathrm{P}}=\overrightarrow{\mathrm{V}}_{\mathrm{G}}+\vec{\Omega}
\wedge \overrightarrow{\mathrm{GP}}\) ,则有速度螺旋分布:
\[
\left[\mathrm{V}_{\Sigma}\right]=\left| \begin{aligned}&
\vec{\Omega} \\& \vec{V}_{\mathrm{G}}\end{aligned}\right.
\]
一般来说,对于非刚体的结构的位移场不是等投影的,对于微小位移和微小旋转,定义位移螺旋分布:
\[
\left[\mathrm{U}_{\Sigma}\right]=\left | \begin{aligned}&a ...
RDM Chapitre 2 量化应力 Dimensionnement Contrainte
RDM Chapitre
2 量化应力 Dimensionnement Contrainte
圣韦南假设
奇异截面 Sections singulières 之外,应力 contraintes
只和内力相关
圣韦南问题
假设:
横截面恒定的直梁
同质弹性各向同性材料
载荷:\(\Sigma_1\)上的扭矩\([F]\),\(\Sigma_1\)上的\([F_0]\),\([F]+[F_0]=[0]\)
SL上没有载荷
目标:
定义一个静态可接受的\(σ(P)\)场,满足应力的兼容性方程(Beltrami)
应力
\[
\sigma(\mathrm{P})=\left[\begin{array}{ccc}\sigma_{11} & \sigma_{12}
& \sigma_{13} \\\sigma_{12} & 0 & 0 \\\sigma_{13} & 0
& 0\end{array}\right]
\]
正应力:\(\sigma_{\mathrm{n}}=\sigm ...
RDM Chapitre 1 结构力学模型 Modѐlisation des structures en efforts
RDM
Chapitre 1 结构力学模型 Modѐlisation des structures en efforts
力螺旋 Torseur
速度场 Champ des vitesse
\[
[V(A)]=\left| \begin{aligned}& \vec{\Omega}\text { (角速度) }
\\& \vec{V}(A)\end{aligned}\right.
\]
位移向量分配
Le Torseur distributeur des déplacements
\[
[U(A)]=\left|\begin{aligned}&{\vec{w}}(\text { vecteur rotation })
\\&{\vec{u}(A)}\end{aligned}\right.
\]
力螺旋
\[
\begin{aligned}
\vec{M}(B) & =\vec{M}(A)+\vec{R} \wedge \overrightarrow{A B} \\
[T(A)] & =\left|\be ...
MMC Chapitre 4 能量分析
MMC Chapitre 4 能量分析
问题的一般形式 Problémes
réguliers
\(S_u\):已知位移的部分
\(S_F\):已知所受面积力的部分,包括面积力为零(Libre)
连续介质力学方程
\[
\left\{\begin{aligned}& \sum_{\mathrm{j}=1,3} \frac{\partial
\sigma_{i j}}{\partial x_j}+\rho f_i=0 \quad i=1,2,3 \\&
\varepsilon_{i j}=\frac{1}{2}\left(\frac{\partial u_i}{\partial
x_j}+\frac{\partial u_j}{\partial x_i}\right) \\&
\underline{\underline{\sigma}}=\lambda
\operatorname{trace}(\underline{\underline{\varepsilon}})
\underline{\underline{I}}+2 \m ...