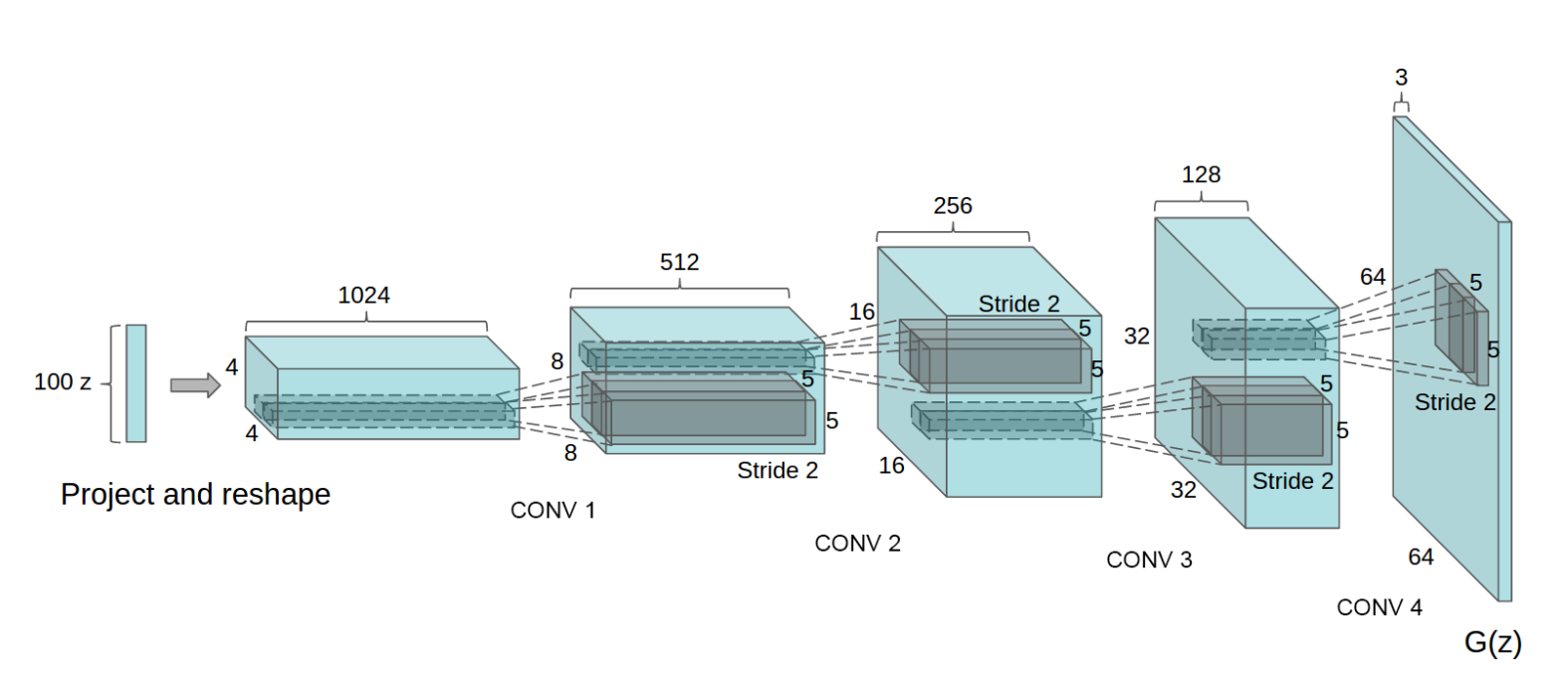
C3 基于状态空间方法的系统控制 Commande des systèmes par approche d’état
C3 基于状态空间方法的系统控制 Commande des systèmes par approche d’état
PLAN
- 校正器的作用
- 基于极点配置的状态反馈控制(尤其是SISO情形)
- 线性二次型控制(LQ)
- 积分作用控制
- 结论
C3.1 校正器的作用 Rôle du correcteur
C3.1.1 对于受控系统的要求 demandées à un système asservi
- 稳定性 stabilité:稳定一个本质上不稳定的系统,并确保系统具有正确的阻尼。
- 快速性 rapidité:保证系统的动态行为,提供令人满意的响应时间。
- 精确性 précision(静态或动态):减少或消除相对于所需参考值的误差。 一个控制系统确保稳定性、快速性和精确性之间的折中。
稳定性
稳定性取决于演化矩阵的谱,我们在上一章已经讨论。
快速性
对于二阶系统,使用超调量\(D\),第一最大值时间\(t_m\),响应时间\(t_r\)等参数衡量快速性。
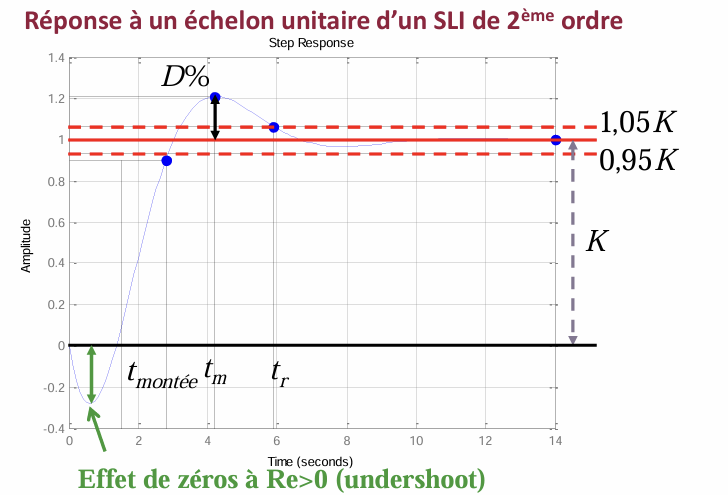
超调量
overshoot\[ D=\frac{y_{\max }-y_{s t}}{y_{s t}}=\exp \left(-\frac{\pi \zeta}{\sqrt{1-\zeta^2}}\right) \]
欠调量
undershoot\[ y_{\text {undershoot }}=\sup (-y(t)) \]
响应时间
Temps de réponse\[ t_r \Rightarrow \text { bande de } \pm 5 \% \text { du } y_{s t} \]
上升时间
Temps de montée\[ t_{\text {monteer }} \Rightarrow \text { de 0,1à } 0,9 \text { du } y_{s t} \]
第一个最大值时间
Temps du 1ermaximum
\[ t_m=\frac{\pi}{\omega_0 \sqrt{1-\zeta^2}} \Rightarrow \omega_0 t_m \cong 3 \]
精确性
在稳态下输出和设定值 la consigne
之间没有偏差écart(即使存在扰动perturbation)。
C3.1.2 闭环控制系统的状态
考虑一个线性时不变系统:
\[ \begin{aligned}& \dot{x}(t)=A x(t)+B u(t) \\& y(t)=C x(t) .\end{aligned} \]
假设其系统如下:
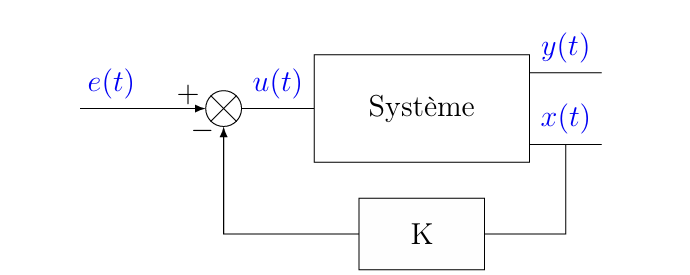
其中,\(K\)称为状态反馈矩阵retour d’état。那么有:\(u(t)=-K x(t)+e(t)\),因此系统可以写作:
\[ \begin{aligned} & \dot{x}(t)=(A-B K) x(t)+B e(t) \\ & y(t)=C x(t) \end{aligned} \]
通过这种控制,我们将矩阵 \(A\) 修改为 \(A - BK\)。状态反馈控制因此影响了系统的动态行为,系统现在依赖于 \(A - BK\) 的特征值。状态反馈矩阵 \(K\) 可以让我们选择期望的特征值,而新的输入 \(e\) 则可以用来控制系统的稳态行为。
一些定义
对于一个闭环控制系统:
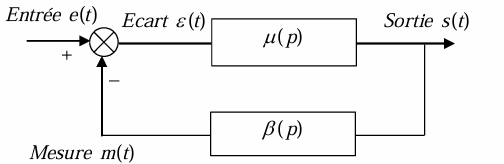
其开环传递函数Fonction de transfert en boucle ouverte为:
\[ \operatorname{FTBO}(p)=\frac{M(p)}{\varepsilon(p)}=\mu(p) \beta(p) \]
其闭环控制函数Fonction de transfert en boucle fermée为:
\[ \operatorname{FTBF}(p)=\frac{S(p)}{E(p)}=\frac{\mu(p)}{1+\mu(p) \beta(p)} \]
其截止频率Pulsation de coupure
为开环传递函数为\(1\)是对应的频率:
\[ \left|F T B O\left(j \omega_c\right)\right|=1(0 \mathrm{~dB}) \]
所有开环传递函数值大于\(1\)的频率的集合\(\left\{\omega:\left|T_{B O}(j
\omega)\right|>1\right\}\)称为导带bande passante。
C3.2 基于极点配置的状态反馈控制(尤其是SISO情形)Commande retour d’état par placement de pôles (notamment cas SISO)
C3.2.1 极点配置 placement de pôles
继续考虑状态方程:
\[ \dot{\mathbf{x}}(t)=(\mathbf{A}-\mathbf{B} \mathbf{K}) \mathbf{x}(t)+\mathbf{B} \mathbf{e}(t) \]
极点配置法希望通过选择闭环系统矩阵\(\mathbf{A}-\mathbf{B K}\)的特征值来计算矩阵\(\mathbf{ K }\)。根据前一章的研究结果,有:
\[ \begin{aligned}&\mathbf{x}(t)=e^{(\mathbf{A}-\mathbf{B K})\left(t-t_0\right)} \mathbf{x}\left(t_0\right)=\sum_{i=1}^n \alpha_i e^{\lambda_i\left(t-t_0\right)} \quad \\&\lambda_i=spectrum(\mathbf{A}-\mathbf{B K})\end{aligned} \]
因此,可以通过选择合适的特征值来塑造系统相应特征。
C3.2.2 Wonham定理
Wonham定理:对于任意选择的特征值集合 \(\left\{\lambda_1, \ldots, \lambda_n\right\}\) ,其中每个 \(\lambda_i\) 要么是实数,要么是另一个特征值 \(\lambda_j\)的共轭复数,存在一个矩阵 \(\mathbf{K} \in \mathbb{R}\) ,使得矩阵 \(\mathbf{A}-\mathbf{B K}\) 的特征值为 \(\left\{\lambda_1, \ldots, \lambda_n\right\}\) ,当且仅当系统完全可控。
如果系统不是完全可控的,可以通过基变换,将其转换为如下形式(连续时间情况下):·
\[ \binom{\dot{\tilde{x}}_c}{\dot{\hat{x}}_c}=\left(\begin{array}{cc}\tilde{A}_c-\tilde{B}_c \tilde{K}_1 & A_{12}-\tilde{B}_c \tilde{K}_2 \\0 & \hat{A}_c\end{array}\right)\binom{\tilde{x}_c}{\hat{x}_c}+\binom{\tilde{B}_1}{0} e . \]
此时,演化矩阵的特征值一定包括\(\hat{A}_c\)的特征值。
C3.2.3 特征值的选择和状态反馈矩阵K的计算
特征值的选择
闭环系统的特征值选择十分复杂,因为极点位置无法直接得出系统在参数变化时的鲁棒性。这种选择通常依赖于设计者的经验。一般遵循以下规则和经验:
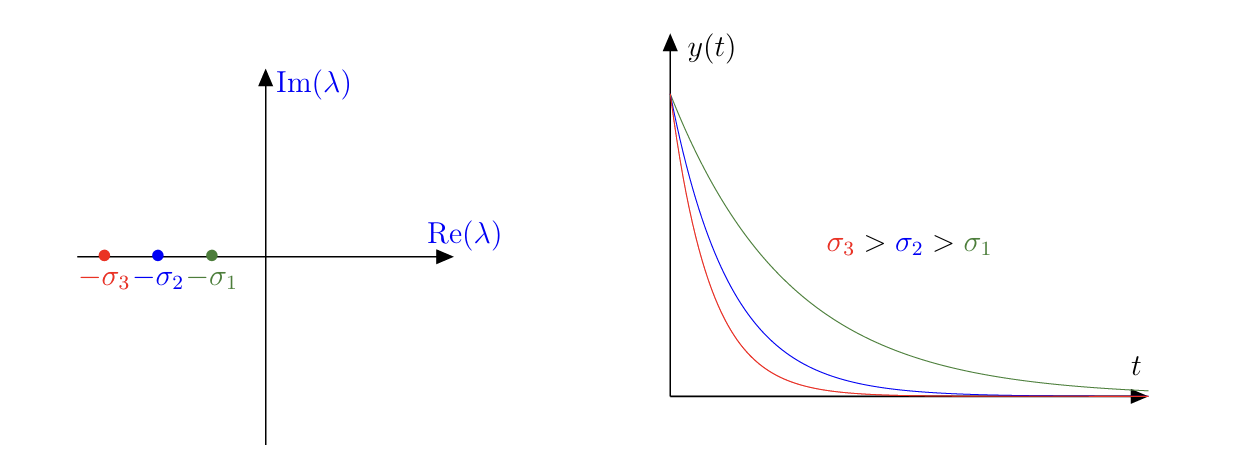
- 闭环稳定性
stabilité en boucle fermée要求所有特征值的实部为负。 - 一个负实特征值 \(\lambda_i=-\sigma_i\left(\sigma_i>0\right)\) 会在闭环系统的响应中引入一个暂态分量 \(e^{-\sigma_i t}\) ,其收敛速度与 \(\sigma_i\) 成正比, \(\sigma_i\) 越大,收敛越快。
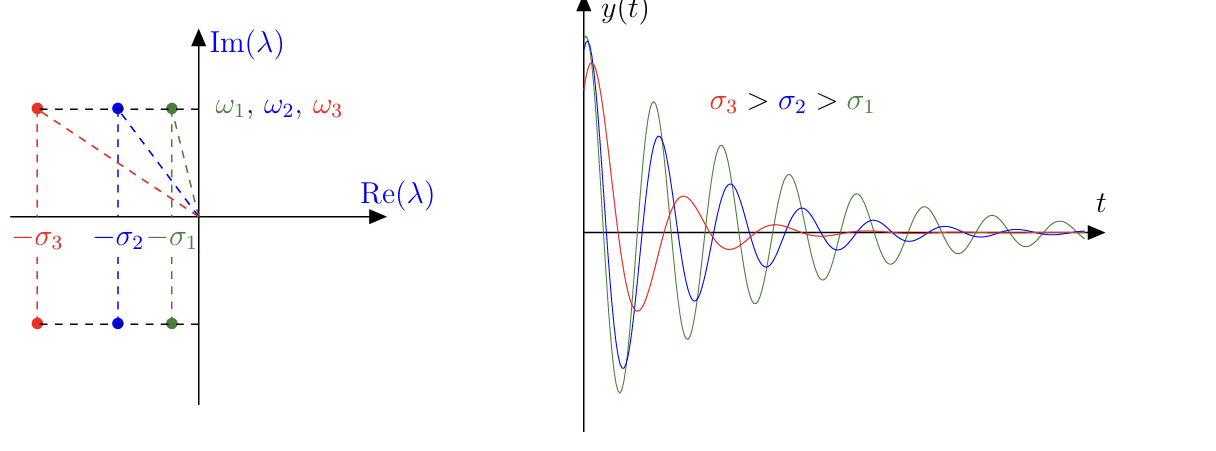
- 一个复数特征值及其共轭复数 \(\lambda_i=-\sigma_i \pm j \omega_i\) 会导致系统出现振荡衰减响应,形式为 \(e^{-\sigma_i t} \sin \left(\omega_i t\right)\) 。 \(\sigma_i\) 越大,衰减越快, \(\omega_i\) 越大,振荡频率越高。阻尼系数由以下关系式给出:
\[ \xi_i=\frac{\sigma_i}{\sqrt{\sigma_i^2+\omega_i^2}} \]
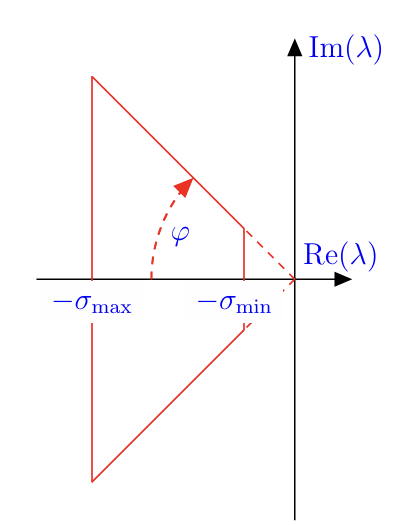
- 可以定义一个类似于梯形的区域(见图3.4),该区域用于确定合理的特征值位置,确保系统快速性和阻尼:
- \(-\sigma_{\min }\) 确定了最小快速性;
- \(-\sigma_{\max }\) 确定了最大快速性(以限制执行器的工作强度);
- 一个角度 \(\varphi\) 使得 \(\cos (\varphi)=\xi\) ,定义了最小的阻尼比。
计算状态反馈矩阵
在选择特征之后,可以通过特征多项式来计算状态反馈矩阵:
\[ |\lambda \mathbf{I}-(A-B K)| \equiv \prod_{i=1}^n\left(\lambda-\lambda_i\right) \]
使用Matlab计算
最简单的方法是直接通过Matlab的place或acker命令计算。
place命令用于计算状态反馈矩阵 \(K\),使得闭环系统的极点位于指定的位置。它通过求解控制系统的极点分配问题,提供精确的极点配置。
语法:
1 | K = place(A, B, p) |
- 其中
p: 指定的期望闭环极点向量。K: 状态反馈矩阵。
acker 命令基于
Ackermann’s formula(阿克曼公式)来计算状态反馈增益矩阵
K,使系统的闭环极点位于给定的期望值。它用于线性系统的极点配置。
语法:
1 | K = acker(A, B, p) |
单变量系统
考虑一个单变量系统:\(\dot{x}(t)=A x(t)+B u(t)\),其中:
\[ A=\left(\begin{array}{ccccc}0 & 1 & 0 & \ldots & 0 \\0 & 0 & 1 & \ldots & 0 \\\vdots & \vdots & \vdots & \ddots & \vdots \\0 & 0 & 0 & \ldots & 1 \\-a_0 & -a_1 & -a_2 & \ldots & -a_{n-1}\end{array}\right), \quad B=\left(\begin{array}{c}0 \\0 \\\vdots \\0 \\1\end{array}\right) \]
设\(u(t)=-K x(t)+e(t)\)。\((A,B)\)是可控的,所以控制矩阵是满秩的。
伴随矩阵 \(A\)这种满足主对角线上方的第一条对角线上的元素全为 1,其他元素则为 0,矩阵的最后一行包含了其特征多项式的系数 \(p(x)=x^n+a_{n-1} x^{n-1}+\ldots+a_1 x+a_0\) 的矩阵称之为伴随矩阵。
矩阵\(A\)的特征多项式:
\[ \operatorname{det}(\lambda I-A)=\lambda^n+a_{n-1} \lambda^{n-1}+\cdots+a_1 \lambda+a_0 \]
状态反馈矩阵(因为输入是一维的):
\[ K=\left(k_1, k_2, \ldots, k_n\right) \]
因此,有:
\[ A-B K=\left(\begin{array}{ccccc} 0 & 1 & 0 & \ldots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & 1 \\ -a_0-k_1 & -a_1-k_2 & -a_2-k_3 & \ldots & -a_{n-1}-k_n \end{array}\right) \]
其特征多项式为:
\[ \operatorname{det}(\lambda I-(A-B K))=\lambda^n+\left(a_{n-1}+k_n\right) \lambda^{n-1}+\cdots+\left(a_1+k_2\right) \lambda+\left(a_0+k_1\right) \]
在选择特征值之后,有特征多项式
\[ P_{\mathrm{des}}(\lambda)=\prod_{j=1}^n\left(\lambda-\lambda_j\right)=\lambda^n+b_{n-1} \lambda^{n-1}+\cdots+b_1 \lambda+b_0 \]
因此有:
\[ K=\left(b_0-a_0, b_1-a_1, \ldots, b_{n-1}-a_{n-1}\right) \]
Bass-Gura公式
对于多变量系统,首先定义\(x=T \tilde{x} \text { , } T=\mathcal{C} \tilde{\mathcal{C}}^{-1}\),将状态方程转化为伴随形式:
\[ \begin{gathered}\dot{\tilde{x}}(t)=\tilde{A} \tilde{x}(t)+\tilde{B} u(t), \\\tilde{A}=\left(\begin{array}{ccccc}0 & 1 & 0 & \ldots & 0 \\0 & 0 & 1 & \ldots & 0 \\\vdots & \vdots & \vdots & \ddots & \vdots \\0 & 0 & 0 & \ldots & 1 \\-a_0 & -a_1 & -a_2 & \ldots & -a_{n-1}\end{array}\right), \quad \tilde{B}=\left(\begin{array}{c}0 \\0 \\\vdots \\0 \\1\end{array}\right) .\end{gathered} \]
有:\(\tilde{A}=T^{-1} A T \text { , } \tilde{B}=T^{-1} B\)。通过与上述方法相同的思路,伴随形式的反馈矩阵:
\[ \tilde{K}=\left(b_0-a_0, b_1-a_1, \ldots, b_{n-1}-a_{n-1}\right) \]
原本的反馈矩阵为:
\[ \begin{aligned}K&=\tilde{K} T^{-1}=\left(b_0-a_0, b_1-a_1, \ldots, b_{n-1}-a_{n-1}\right) T^{-1} \\&=\left(b_0-a_0, b_1-a_1, \ldots, b_{n-1}-a_{n-1}\right)\left(C \tilde{C}^{-1}\right)^{-1}\end{aligned} \]
Ackermann公式
对于一个单变量且完全可控的系统,给定系统的控制矩阵,有:
\[ K=\left(\begin{array}{lllll}0 & 0 & \ldots & 0 & 1\end{array}\right) \mathcal{C}^{-1} P(A) \]
其中:
\[ \mathcal{P}(\mathbf{A})=\mathbf{A}^n+\alpha_1 \mathbf{A}^{n-1}+\cdots+\alpha_{n-1} \mathbf{A}+\alpha_n \mathbf{I}_n \]
\(\alpha_i\)是特征值多项式\(\left(\lambda-\lambda_1\right) \cdots\left(\lambda-\lambda_n\right)=\lambda^n+\alpha_1 \lambda^{n-1}+\cdots+\alpha_{n-1} \lambda+\alpha_n\)的系数。
CE3.1 直流电机
直流电机
有:
\[ \begin{aligned}& x_1=y(t)=\frac{1}{s} x_2 \\& x_2=\frac{G}{s+a} u(t)\end{aligned} \]
因此有:
\[ \begin{aligned}&sx_1 = x_2\\&s x_2+a x_2=G u(t)\end{aligned} \]
即为:
\[ \begin{aligned}&\dot{x}_1=x_2\\&\dot{x}_2=-a x_2+G u(t)\end{aligned} \]
因此,系统状态方程为:
\[ \begin{gathered} \dot{x}(t)=\left(\begin{array}{cc} 0 & 1 \\ 0 & -a \end{array}\right) x(t)+\binom{0}{G} u(t) \\ y(t)=\left(\begin{array}{ll} 1 & 0 \end{array}\right) x(t) \end{gathered} \]
希望设计控制器,使得电机的角位置 \(y\) 能够在没有稳态误差的情况下跟踪阶跃指令 \(y_c(t)=Y_0 \Gamma(t)\) ,并且具有瞬态响应特性,超调量 \(D=20 \%\) ,最大时间 \(t_m= 10 ms\) 。
考虑反馈控制:
\[ u(t)=-\left(\begin{array}{ll} k_1 & k_2 \end{array}\right) x(t)+M y_c(t) . \]
有系统状态方程变为:
\[ \dot{x}(t)=\left(\begin{array}{cc}0 & 1 \\-G k_1 & -\left(a+G k_2\right)\end{array}\right) x(t)+\binom{0}{M G} y_c(t) \]
为了使闭环系统的行为与二阶系统一致,特征方程为:
\[ P(\lambda)=\lambda^2+\left(a+G k_2\right) \lambda+G k_1 \equiv \lambda^2+2 \xi \omega_0 \lambda+\omega_0^2 \text {. } \]
根据要求,使用超调量求得\(\xi=0.45\),使用最大响应时间和\(\xi=0.45\),求得\(\omega_0=350 \mathrm{rad} \cdot \mathrm{~s}^{-1}\)。因此可得:
\[ \begin{aligned} k_1 & =\frac{\omega_0^2}{G}=\frac{350^2}{G}=\frac{122500}{G} \\ k_2 & =\frac{2 \xi \omega_0-a}{G}=\frac{315-a}{G} \end{aligned} \]
值得注意的是,我们并没有准确的求出极值点,而是利用了二阶系统的一些性质。
接下来,由于\(y_c(t)=Y_0\)时,系统应该平稳,即:
\[ \binom{0}{0}=\left(\begin{array}{cc}0 & 1 \\-G k_1 & -\left(a+G k_2\right)\end{array}\right) x_{\infty}+\binom{0}{M G} Y_0 \]
从而得出:
\[ x_{2 \infty}=0, \quad x_{1 \infty}=\frac{M Y_0}{k_1} \]
即可求得\(M=k_1\)。
CE3.2 倒立摆问题
回忆上一章中多次讨论的倒立摆问题,其状态方程为:
\[ \begin{aligned}&A=\left(\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & \frac{m g}{M} & 0 & 0 \\ 0 & \frac{(m+M) g \cos \bar{x}_2}{M l} & 0 & 0 \end{array}\right), \quad \\&B=\left(\begin{array}{c} 0 \\ 0 \\ \frac{1}{M} \\ \frac{\cos \bar{x}_2}{M l} \end{array}\right), \quad C=\left(\begin{array}{llll} 1 & 0 & 0 & 0 \end{array}\right), \quad D=0\end{aligned} \]
我们已经证明过,经过线性化之后的该系统可控,其控制矩阵满秩。设:
\[ u(t)=-K x(t)+e(t), \ \ K = (k1 \ k2 \ k3 \ k4) \]
我们曾经讨论过其开环系统特征值:
\[ \left\{0,0,-\sqrt{\frac{(m+M) g}{M l}},+\sqrt{\frac{(m+M) g}{M l}}\right\} \]
- 保持负特征值不变为 \(-\sqrt{\frac{(m+M) g}{M l}}\) ;
- 将正特征值变为其相反数 \(-\sqrt{\frac{(m+M) g}{M l}}\);
- 将另外两个特征值选为模为 \(\frac{1}{2} \sqrt{\frac{(m+M) g}{M l}}\) 的一对复数,并使其阻尼系数为 \(\xi=0.7\) ,即特征值为 \(\frac{1}{2} \sqrt{\frac{(m+M) g}{M l}}(-1 \pm j)\) 。
考虑\(A-BK\):
\[ \begin{aligned}A-B K=&\left(\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & \frac{m g}{M} & 0 & 0 \\ 0 & \frac{(m+M) g}{M l} & 0 & 0 \end{array}\right)-\left(\begin{array}{c} 0 \\ 0 \\ \frac{1}{M} \\ \frac{1}{M l} \end{array}\right)\left(\begin{array}{llll} k_1 & k_2 & k_3 & k_4 \end{array}\right)\\&=\left(\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -\frac{k_1}{M} & \frac{m g}{M}-\frac{k_2}{M} & -\frac{k_3}{M} & -\frac{k_4}{M} \\ -\frac{k_1}{M l} & \frac{(m+M) g}{M l}-\frac{k_2}{M l} & -\frac{k_3}{M l} & -\frac{k_4}{M l} \end{array}\right)\end{aligned} \]
其特征值多项式:
\[ \begin{aligned}\operatorname{let}(\lambda I-(A-B K)) & =\left|\begin{array}{cccc}\lambda & 0 & -1 & 0 \\0 & \lambda & 0 & -1 \\\frac{k_1}{M} & -\frac{m g}{M}+\frac{k_2}{M} & \lambda+\frac{k_3}{M} & \frac{k_4}{M} \\\frac{k_1}{M l} & -\frac{(m+M) g}{M l}+\frac{k_2}{M l} & \frac{k_3}{M l} & \lambda+-\frac{k_4}{M l}\end{array}\right| \\& =\lambda^4+\left(\frac{k_3}{M}+\frac{k_4}{M l}\right) \lambda^3+\left(\frac{k_1}{M}+\frac{k_2}{M l}-\frac{(m+M) g}{M l}\right) \lambda^2-\frac{g k_3}{M l} \lambda-\frac{g k_1}{M l}\end{aligned} \]
同时,根据我们选择的特征值计算特征多项式:
\[ \begin{aligned} & \operatorname{det}(\lambda I-(A-B K))=\left(\lambda+\sqrt{\frac{(m+M) g}{M l}}\right)^2\left(\lambda^2+\sqrt{\frac{(m+M) g}{M l}} \lambda+\frac{(m+M) g}{2 M l}\right) \\ & =\lambda^4+3 \sqrt{\frac{(m+M) g}{M l}} \lambda^3+3,5 \frac{(m+M) g}{M l} \lambda^2+2 \frac{(m+M) g}{M l} \sqrt{\frac{(m+M) g}{M l}} \lambda+0,5\left(\frac{(m+M) g}{M l}\right)^2 . \end{aligned} \]
可解得:
\[ \begin{array}{ll}k_1=-0,5 \frac{(m+M)^2 g}{M l} & k_3=-2(m+M) \sqrt{\frac{(m+M) g}{M l}} \\k_2=4,5(m+M) g+0,5 \frac{(m+M)^2 g}{M} & k_4=(2 m+5 M) \sqrt{\frac{(m+M) g l}{M}}\end{array} \]
C3.2.4 在输入端添加增益以保证稳态
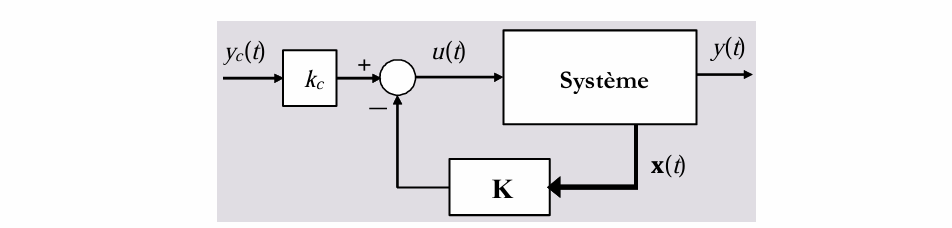
增加增益\(k_c\)后,系统变为:
\[ \left\{\begin{array}{l}\dot{\mathbf{x}}(t)=(\mathbf{A}-\mathbf{B} \mathbf{K}) \mathbf{x}(t)+\mathbf{B} k_c y_c(t) \\y(t)=\mathbf{C} \mathbf{x}(t)\end{array}\right. \]
在稳态时,应有\(y(t)=y_c(t)\),\(\dot{\mathbf{x}}(t) = 0\)。因此有:
\[ k_c=\frac{-1}{\mathbf{C}(\mathbf{A}-\mathbf{B} \mathbf{K})^{-1} \mathbf{B}} \]
C3.2.5 增加与扰动有关的增益以保证稳态
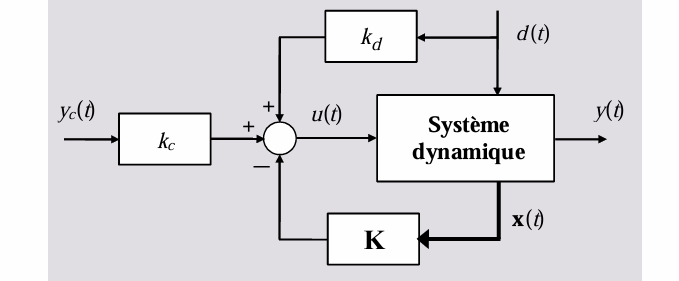
此时控制律:
\[ u(t)=-\mathbf{K x}(t)+k_c y_C(t)+k_d d(t) \]
闭环状态:
\[ \left\{\begin{array}{l} \dot{\mathbf{x}}(t)=(\mathbf{A}-\mathbf{B K}) \mathbf{x}(t)+\mathbf{B} k_c y_c(t)+\left(\mathbf{B} k_d+\mathbf{B}^{\prime}\right) d(t) \\ y(t)=\mathbf{C} \mathbf{x}(t) \end{array}\right. \]
此时,两个增益满足:
\[ \begin{aligned} & k_c=-\left[\mathbf{C}(\mathbf{A}-\mathbf{B K})^{-1} \mathbf{B}\right]^{-1} \\ & k_d=-\left[\mathbf{C}(\mathbf{A}-\mathbf{B K})^{-1} \mathbf{B}\right]^{-1}\left[\mathbf{C}(\mathbf{A}-\mathbf{B K})^{-1} \mathbf{B}^{\prime}\right] \end{aligned} \]
3.2.6 部分可控系统的闭环控制
当系统部分可控时,也可以控制系统的可控模态。基于卡尔曼标准形式,演化矩阵和输入矩阵分别为:
\[ A=\left(\begin{array}{cc}A_c & A_{12} \\0 & A_{\bar{c}}\end{array}\right), \quad B=\binom{B_c}{0} \]
考虑但输入系统,此时系统的闭环控制形式
la commande par retour d'état 为:
\[ u(t)=-\left(\begin{array}{ll}K_1 & K_2\end{array}\right) x(t)+M y_c(t)=-K_1 x_1(t)-K_2 x_2(t)+M y_c(t) \]
其中,\(K_1 \in \mathbb{R}^q \text { ,} K_2 \in \mathbb{R}^{n-q}\)。演化方程可以写作:
\[ \begin{aligned}&\dot{x}(t)=(A-B K) x(t)+B M y_c(t), \\& A-B K=\left(\begin{array}{cc}A_c-B_c K_1 & A_{12}-B_c K_2 \\0 & A_{\bar{c}}\end{array}\right)\end{aligned} \]
此时,闭环系统的特征值可由一下公式计算:
\[ \begin{gathered}\operatorname{det}(\lambda I-(A-B K))=\operatorname{det}\left(\lambda I-\left(A_c-B_c K_1\right)\right) \operatorname{det}\left(\lambda I-A_{\bar{c}}\right)=0\end{gathered} \]
这一表达式表明,只有 \(q\) 个特征值可以通过设计反馈矩阵 \(K_1\) 任意调整,而状态向量的 \(x_2\) 部分 (维度为 \(n-q\) ) 的特征值则保持不变,闭环控制对其无影响。
3.2.7 总结
- 状态反馈与极点配置控制律
Loi par retour d’état et par placement de pôles:
\[ u(t)=-K x(t)+k_c y_c(t)+k_d d(t) \]
- 设计步骤 (SISO 系统情况下) :
- 假设:
- 系统是可控的(或至少是可稳定化的)。
- 所有状态都是可测量的。
- 假设扰动 \(d(t)\) 是可测量的。
- 选择闭环系统的期望特征值:
- 根据系统性能要求,选择合适的闭环特征值。
- 计算状态反馈增益 \(K\) :
- 通过极点配置,计算状态反馈增益矩阵 \(K\) 以获得期望的闭环特征值。
- 确定增益 \(k_c\) 和 \(k_d\) :
- 计算增益 \(k_c\) 和 \(k_d\) 以消除稳态埕差,从而在恒定指令下跟踪输出,并抵消恒定扰动的影响。
- 假设:
CE3.3 电磁悬浮系统
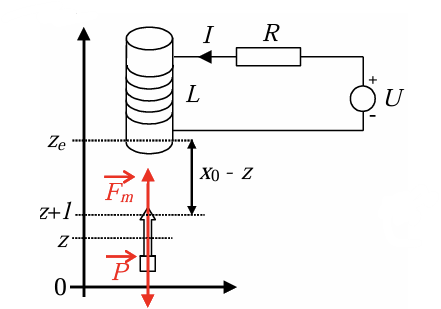
电磁悬浮系统的目标是使用电磁力 \(F_m\) 平衡重力 \(P\) ,并保持物体在某个平衡位置 \(z_e\) 。该系统可通过控制输入电压 \(U(t)\) 作用于电感 \(L\) 、电阻 \(R\) 和电流 \(I(t)\) ,从而调节系统的动态行为。
首先对系统进行建模:
电路方程:基尔霍夫定律
\[ L \frac{d I(t)}{d t}+R I(t)=U(t) \]
力学方程:牛顿第二定律
\[ m \frac{d^2 z(t)}{d t^2}=c \frac{I(t)}{\left(x_0-z(t)\right)^2}-m g \]
其中, \(z(t)\) 是物体的位置, \(I(t)\) 是电流, \(x_0\) 是固定距离, \(g\) 是重力加速度, \(c\) 是电磁力的比例常数。
在平衡点\(\bar{z}=0\)周围线性化
有\(\bar{z}=0\)时,系统平衡:
\[ \left\{\begin{array}{l} \bar{U}=R \bar{I} \\ c \frac{\bar{I}}{x_0{ }^2}-m g=0 \end{array}\right. \]
可得平衡点的电压电流:
\[ \left\{\begin{array}{l}\bar{I}=\frac{m g x_0{ }^2}{c}=i_0 \\\bar{U}=R \bar{I}=R i_0\end{array}\right. \]
在平衡点附近,电压和电流可以表示为:
\[ \left\{\begin{array}{l} I(t)=\bar{I}+i_1(t) \\ U(t)=\bar{U}+u_1(t) \end{array}\right. \]
进而带入状态方程,同时认为\(z(t)\rightarrow \bar{z} = 0\),得到”
\[ \left\{\begin{array}{l}L \frac{d \dot{i}_1(t)}{d t}+R \dot{i}_1(t)=u_1(t) \\\frac{d^2 z(t)}{d t^2}=\frac{g}{i_0} i_1(t)+\frac{2 g}{x_0} z(t)\end{array}\right. \]
设系统的状态向量:
\[ \mathbf{x}(t)=\left(\begin{array}{l} \dot{i}_1(t) \\ z(t) \\ \dot{z}(t) \end{array}\right) \]
带入数值:
\[ \begin{aligned}R =10 \Omega ,L =0,01 H ,g =10 \mathrm{~m} \cdot \mathrm{~s}^{-2} ,i_0 =0,5 \mathrm{~A} ,x_0 =0,0125 \mathrm{~m} ,\beta =4000 \mathrm{~V} \cdot \mathrm{~m}^{-1}\end{aligned} \]
即可得到线性化之后的系统状态方程:
\[ \begin{aligned} &\frac{d}{d t}\left(\begin{array}{l} \dot{i}_1(t) \\ z(t) \\ \dot{z}(t) \end{array}\right) =\bar A x(t)+\bar Bu_1(t)\\&=\left(\begin{array}{ccc} -1000 & 0 & 0 \\ 0 & 0 & 1 \\ 20 & 1600 & 0 \end{array}\right)\left(\begin{array}{c} \dot{i}_1(t) \\ z(t) \\ \dot{z}(t) \end{array}\right)+\left(\begin{array}{c} 100 \\ 0 \\ 0 \end{array}\right) u_1(t) \\ &V_z(t) =\left(\begin{array}{lll} 0 & 4000 & 0 \end{array}\right)\left(\begin{array}{l} \dot{i}_1(t) \\ z(t) \\ \dot{z}(t) \end{array}\right) \end{aligned} \]
分析开环系统,首先计算开环系统的特征值,得到:
\[ spectre(\bar A) = {-1000,-40,+40} \]
可见系统并不稳定。
然后研究系统可控性,其控制矩阵:
\[ \left[\begin{array}{lll} \mathbf{B} & \mathbf{A B} & \mathbf{A}^2 \mathbf{B} \end{array}\right]=\left[\begin{array}{ccc} 100 & -10^5 & 10^8 \\ 0 & 0 & 2.10^3 \\ 0 & 2.10^3 & -2.10^6 \end{array}\right] \]
满秩,所以可控。
闭环控制方程:
\[ u_1(t)=-\left(\begin{array}{lll}k_1 & k_2 & k_3\end{array}\right)\left(\begin{array}{l}\dot{i}_1(t) \\z(t) \\\dot{z}(t)\end{array}\right)+k_c y_c(t) \]
从而得到闭环状态方程:
\[ \begin{aligned} \frac{d}{d t}\left(\begin{array}{l} \dot{i}_1(t) \\ z(t) \\ \dot{z}(t) \end{array}\right) & =\left(\begin{array}{ccc} -1000-100 k_1 & -100 k_2 & -100 k_3 \\ 0 & 0 & 1 \\ 20 & 1600 & 0 \end{array}\right)\left(\begin{array}{l} \dot{i}_1(t) \\ z(t) \\ \dot{z}(t) \end{array}\right)+\left(\begin{array}{c} 100 k_c \\ 0 \\ 0 \end{array}\right) y_c(t) \\ V_z(t) & =\left(\begin{array}{lll} 0 & 4000 & 0 \end{array}\right)\left(\begin{array}{l} \dot{i}_1(t) \\ z(t) \\ \dot{z}(t) \end{array}\right) \end{aligned} \]
我们希望实现:
- \(D<10 \% \rightarrow \xi=0,6\)
- \(t_m \approx 0,03 \mathrm{~s} \rightarrow \omega_0=130\)
因此,我们保留\(-1000\)这个特征值,并根据\(\left\{\begin{array}{l}\xi=0,6 \\\omega_0=130\end{array}\right.\)写出特征多项式:
\[ |\lambda \mathbf{I}-(\mathbf{A}-\mathbf{B K})|=(\lambda+1000)\left(\lambda^2+2 \times 0,6 \times 130 \lambda+130^2\right) \]
从而计算得到\(k_1=1,560 \quad k_2=9,375.10^3 \quad k_3=87,25\)。
最后,计算\(k_c\):
\[ k_c=-\frac{800+80 k_1-k_2}{4000}=2,125 \]
C3.3 线性二次型控制 Commande Linéaire Quadratique
C3.3.1 连续时间系统的一般结果
对于一个连续时间系统:
\[ \begin{gathered}\dot{x}(t)=A x(t)+B u(t) \\y(t)=C x(t)\end{gathered} \]
并且具有初始条件 \(x(0)\) 。我们寻找一个控制 \(u(t)\) ,使得状态 \(x\) 回到 \(0\),同时最小化准则:
\[ J=\int_0^{\infty}\left(x^{\top} Q x+u^{\top} R u\right) d t \]
其中 \(Q=Q^{\top} \geq 0\) 和 \(R=R^{\top}>0\)
是对称半正定和正定矩阵semi-dé nie et dé nie positives,预先给定。这个表达式可以定性地解释为,将项
\(x^{\top} Q x\) 归因于状态能量
l'énergie de l'état,而将项 \(u^{\top} R u\) 归因于控制能量
l'énergie de la commande。
这种问题被称为线性二次型调节器综合问题problème de la synthèse d'un régulateur LQ
。我们使用李雅普诺夫方程 équations de Lyapunov来解决。
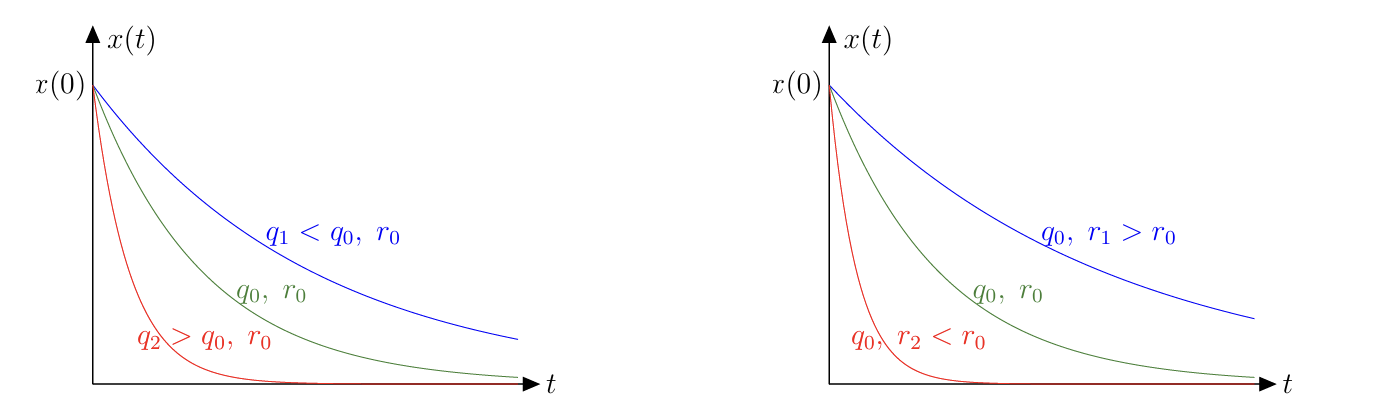
矩阵 \(Q\) 和 \(R\) 是 LQ 控制的调节参数。 考虑对角矩阵 \(Q\) 和 \(R\):
\[ J=\int_0^{\infty}\left(q_1 x_1(t)^2+\ldots+q_n x_n(t)^2+\left(r_1 u_1(t)^2+\ldots+r_m u_m(t)^2\right)\right) d t \]
- 如果增加 \(q_i\) ,闭环系统会变得更快,控制量会增大。
- 如果增加 \(r_i\) ,闭环系统会变得更慢,控制量会减小。
- 注意,关键是 \(\lceil Q / R\rfloor\) 的比率。如果同时将 \(\mathbf{Q}\) 和 \(\mathbf{R}\) 乘以相同的系数,最优控制不变。
这一点可以在之后的例子中看到。
首先假设\(Q=H^{\top} H\),\(H\)是一个满秩矩阵。
正定矩阵
- 一个对称矩阵 \(\mathbf{P}=\mathbf{P}^T\) 是正定矩阵,当且仅当对任意非零向量 \(\mathbf{x} \in \mathbb{R}^n \backslash\{0\}\) ,都有 \(\mathbf{x}^T \mathbf{P} \mathbf{x}>\) 0 。
- 当且仅当矩阵的所有特征值严格为正时,矩阵是正定的。
- 不通过计算特征值,也可以通过判定矩阵的所有顺序主子式\(\left(\mathbf{P}_{i, j}\right), 1 \leq i, j \leq p \text {, pour } p \in\{1, . . n\}\)的行列式为正,来证明矩阵是正定的。
- 半正定矩阵允许特征值为0。
对于正定矩阵,存在唯一的下三角矩阵 \(L\) ,其主对角线上的元素全是正的,使得 \(M=L L^*\) 。其中 \(L^*\) 是 \(L\) 的共轭转置(或转置,在实数域内)。这一分解被称为科列斯基分解
Cholesky decomposition。
定理
如果满足条件 \((A, B)\) 可稳定和 \((A, H)\) 可检测,则线性二次型调节器问题在无限时间下的解为:
\[ \begin{gathered} u(t)=-K x(t) \\ K=R^{-1} B^{\top} P \end{gathered} \]
其中 \(P=P^{\top} \geq 0\)
是黎卡提Riccati方程的唯一半正定解:
\[ A^{\top} P+P A-P B R^{-1} B^{\top} P+Q=0 \]
最优准则的值为:
\[ J^*=x^{\top}(0) P x(0) \]
闭环系统是渐近稳定的。如果进一步 \((A, H)\) 是可观的,则 \(P\) 是正定的。
Matlab
[K, S, E] = lqr(A, B, Q, R),用于设计线性二次型调节器的函数,其中:
- A: 演化矩阵
- B: 控制矩阵
- Q: 状态加权矩阵
- R: 控制输入加权矩阵
- K: 最优反馈增益矩阵
- S: Riccati方程的解
- E: 闭环系统的极点
X = icare(A, B, Q, R),用于求解连续时间代数Riccati方程,其中:
- A: 演化矩阵
- B: 控制矩阵
- Q: 状态加权矩阵
- R: 控制输入加权矩阵
- X: Riccati方程的正定对称解
CE3.4 简单的开环系统的例子
简单的开环系统的例子
对于开环系统:
\[ \dot{x}(t)=-x(t)+u(t) \]
设最小化准则:
\[ J=\int_0^{+\infty}\left(q x_1(t)^2+r u(t)^2\right) d t, \quad q \geq 0, r>0 \]
黎卡提方程:
$$
-2P - r^{-1} P^2+q=0 $$
其解为:
\[ p_{1,2}=\frac{-2 r \pm 2 r \sqrt{1+\frac{q}{r}}}{2}=r\left(-1 \pm \sqrt{1+\frac{q}{r}}\right) \]
只取正解,从而得:
\[ K=-1+\sqrt{1+\frac{q}{r}} \]
原微分方程转化为:
\[ \dot{x}=-x-\left(-1+\sqrt{1+\frac{q}{r}}\right) x=-\sqrt{1+\frac{q}{r}} x \]
从而求得解:
\[ x(t)=e^{A t} x(0)=e^{-\sqrt{1+\frac{q}{r} t}} x(0) \]
C3.3.2 有噪音的情况的结果
在有噪音的情况,系统可以写作:
\[ \dot{x}(t)=A x(t)+B u(t)+v(t) \]
其中\(v(t)\)代表白噪音:
\[ \left\{\begin{array}{l} E\{v(t)\}=0 \\ E\left\{v(t) v(\tau)^T\right\}=V \delta(t-\tau) \end{array}\right. \]
此时,我们希望以下方程能够最小化:
\[ J=\lim _{T \rightarrow+\infty} \mathbb{E}\left\{\frac{1}{T} \int_0^T\left(x(t)^{\top} Q x(t)+u^{\top}(t) R u(t)\right) d t\right\} \]
满足这些准则的最优控制条件与无噪声的确定性情况下相同,解也是一样的。
定理
对于如上描述的系统和最小化准则,其解等同于无限时间域线性二次调节器问题的解,最优准则的值为:
\[ J^*=x^{\top}(0) P x(0)+\operatorname{trace}(V P) \]
C3.3.3 基于输出的准则
对于系统:
\[ \begin{aligned} & \dot{x}(t)=A x(t)+B u(t) \\ & y(t)=C x(t) \end{aligned} \]
最小化准则也可以写作:
\[ J=\int_0^{+\infty}\left(y(t)^T \tilde{Q} y(t)+u(t)^T R u(t)\right) d t \]
其中,\(Q=C^T \tilde{Q} C\)。
CE3.5 两个积分器的例子

两个积分器的例子
系统的状态:
\[ \left\{\begin{array}{l} \dot{x}=\left(\begin{array}{ll} 0 & 1 \\ 0 & 0 \end{array}\right) x+\left(\begin{array}{ll} 1 \\ 0 \end{array}\right) u\\ y = \left(\begin{array}{ll} 1 & 0 \end{array}\right)x \end{array}\right. \]
最小化准则为:
\[ J=\int_0^{+\infty}\left(\left(\begin{array}{ll} q^2 & 0 \\ 0 & 0 \end{array}\right) x(t)^2+r u(t)^2\right) d t, q>0, r>0 \]
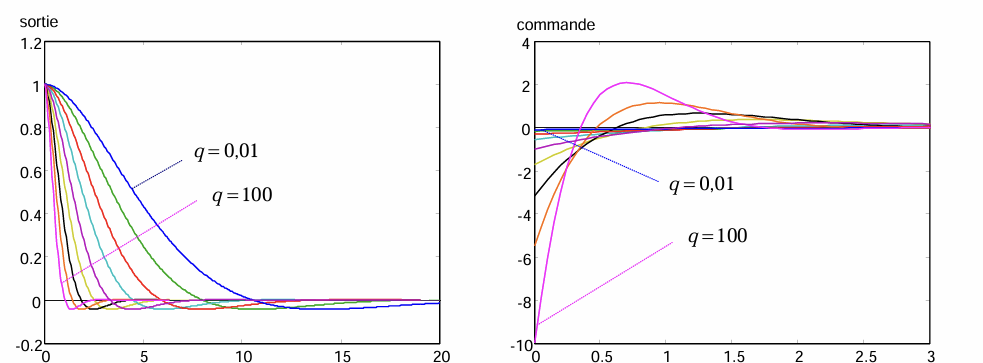
由于状态是一个二维的量,不太方便计算,使用基于输出的准则。
\[ \begin{aligned}J&=\int_0^{+\infty}\left(q y^2+r u(t)^2\right) d t, q>0, r>0\\&=\int_0^{+\infty}\left(q x_1^2+r u(t)^2\right) d t, q>0, r>0\end{aligned} \]
如此进一步的解法与前一个例子完全相同。
CE3.6 飞机横向运动的伺服控制
现在我们将综合考虑一个飞机的横向运动的伺服控制问题。
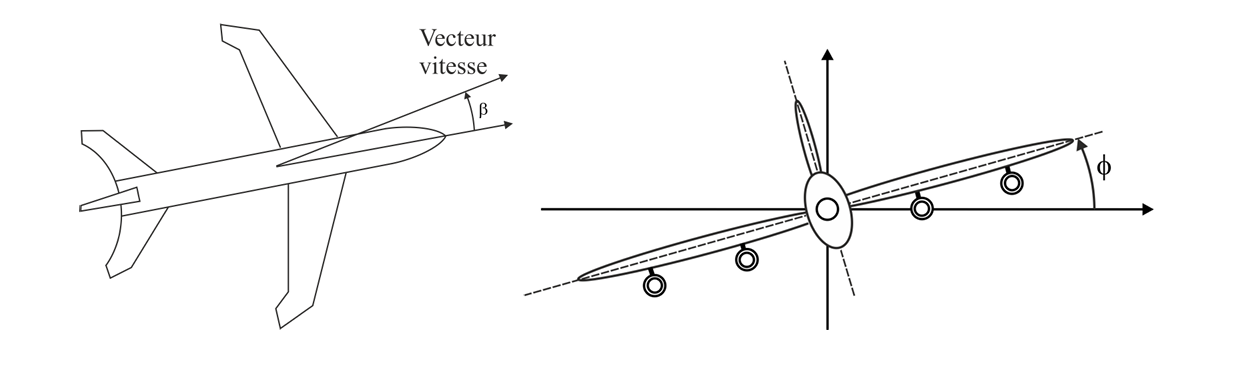
飞机的横向运动通过 4 个状态变量描述 : 侧滑角
angle de dérage\(\beta\) 、滚转速度vitesse de roulis\(p\) 、偏航速度angle de lacet\(r\) 和滚转角angle de roulis\(\phi\) 。状态向量为:\[ x(t)=(\beta(t), p(t), r(t), \phi(t))^T \]
控制量是副翼偏转角
l'angle de braquage des ailerons\(\delta_a\) 和方向舵偏转角l'angle de braquage de la dérive\(\delta_r\) ,即:\[ u(t)=\left(\delta_a(t), \delta_r(t)\right)^T \]
我们假设关注的输出是侧滑角和滚转角:
\[ y(t)=(\beta(t), \phi(t))^T \text { 。 } \]
对于战斗机,横向飞行线性化模型在特定飞行状态下的状态表示为:
\[ A=\left(\begin{array}{cccc}-0.746 & 0.006 & -1 & 0.0369 \\-12.9 & -0.746 & 0.387 & 0 \\4.31 & 0.024 & -0.174 & 0 \\0 & 1 & 0 & 0\end{array}\right), \quad B=\left(\begin{array}{cc}0.0012 & 0.0092 \\6.05 & 0.952 \\-0.416 & -1.76 \\0 & 0\end{array}\right), \quad C=\left(\begin{array}{llll}1 & 0 & 0 & 0 \\0 & 0 & 0 & 1\end{array}\right) \]
该模型是一个具有两个输入、两个输出和 4 个状态变量的MIMO系统。系统的开环特征值为:
- \(-0.7655:\) 一个真实模式,称为纯滚模式,具有较快且稳定的动态;
- \(-0.0062\) : 一个真实模式,称为螺旋模式,动态缓慢且稳定(此模式可能在某些飞行状态下不稳定) ;
- \(-0.4472 \pm i 2.0735\) :称为荷兰滚模式的复数模式,表现为稳定的振荡动态,阻尼系数为 \(\xi=0.21\) 。
进行
Kalman矩阵分析:其控制矩阵:
\[ C =\left(\begin{array}{cccccccc} 0.0012 & 0.0092 & 0.4514 & 1.7588 & -0.3644 & -1.6548 & -1.7089 & -6.4300 \\ 6.0500 & 0.9520 & -4.6898 & -1.5100 & -2.2383 & -21.4200 & 7.0649 & 40.2207 \\ -0.4160 & -1.7600 & 0.2228 & 0.3687 & 1.7942 & 7.4802 & -1.9365 & -8.9477 \\ 0 & 0 & 6.0500 & 0.9520 & -4.6898 & -1.5100 & -2.2383 & -21.4200 \end{array}\right) \]
其观测矩阵:
\[ O =\left(\begin{array}{cccc}1.0000 & 0 & 0 & 0 \\0 & 0 & 0 & 1.0000 \\-0.7460 & 0.0060 & -1.0000 & 0.0369 \\0 & 1.0000 & 0 & 0 \\-3.8309 & 0.0039 & 0.9223 & -0.0275 \\-12.9000 & -0.7460 & 0.3870 & 0 \\6.7821 & -0.0313 & 3.6719 & -0.1414 \\20.9148 & 0.4884 & 12.5440 & -0.4760\end{array}\right) \]
两个矩阵的秩都为\(4\),因此系统完全可控,完全可观。
现在,我们希望通过控制副翼和方向舵的偏转角,使角度 \(\beta\) 和 \(\phi\) 达到设定值,并在初始条件下实现约\(3\)秒的响应时间,且控制量的幅度不超过初始条件的 \(2\) 倍。
注意,角度变量 \(\beta\) 和 \(\phi\) 以及控制量 \(\delta_a\) 和 \(\delta_r\) 的单位相同,且大小相当。
为了简化合成问题,我们可以使用对角权重矩阵 \(Q=\operatorname{diag}\left(q_1, q_2, q_3, q_4\right)\) 和 \(R=\operatorname{diag}\left(r_1, r_2\right)\) 。准则为:
\[ J=\int_0^{\infty}\left(q_1 \beta(t)^2+q_2 p(t)^2+q_3 r(t)^2+q_4 \phi(t)^2+r_1 \delta_a(t)^2+r_2 \delta_r(t)^2\right) d t \]
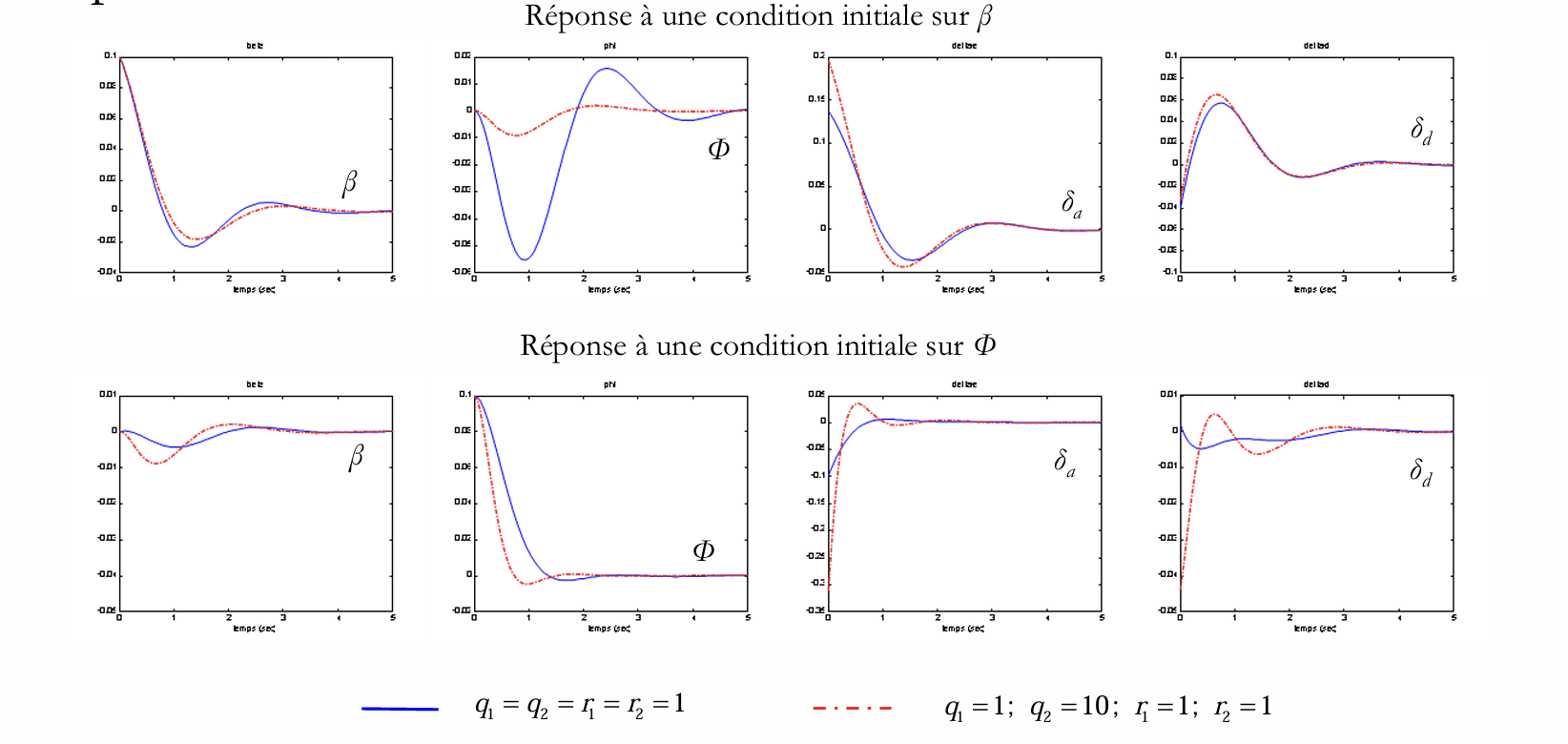
由于我们调节的变量是 \(\beta\) 和 \(\phi\) ,为了简化合成,首先可以设 \(q_2=q_3=0\) 。经过第一次迭代,我们选择了以下两个调节方案:
在初始条件\(\beta=0 , \phi=1\)与\(\beta=0 , \phi=1\)两种情况下,两个调节方案的响应结果如图所示。
可以清楚地看到,第二种调节方案的响应速度更快,但代价是控制量略微增大。对于这两种调节方案,响应时间和控制量的最大幅度都满足设计规范的要求。
C3.3.4 使x趋近于x_c而不是0,以及可测量扰动及其抑制的情况的进一步讨论 Cas des perturbations mesurables et leurs rejet
\(x → x_c\)的情况
首先讨论如何将状态\(x\)带回到某一状态\(x_c\),而不是在此之前我们讨论的带回\(0\)。
系统:
\[ \begin{gathered} \dot{x}(t)=A x(t)+B u(t) \\ y(t)=C x(t) \end{gathered} \]
在稳态时,我们希望\(x\rightarrow x_c\),因此有:
\[ \begin{gathered} 0=A x_c+B u_c \\ y_c=C x_c \end{gathered} \]
令两组方程相减,得到:
\[ \begin{gathered} \dot{x}(t)=A\left(x(t)-x_c\right)+B\left(u(t)-u_c\right) \\ y(t)-y_c=C\left(x(t)-x_c\right) \end{gathered} \]
再定义:\(\tilde{x}(t)=x(t)-x_c, \tilde{u}(t)=u(t)-u_c, \tilde{y}(t)=y(t)-y_c\),有新的状态方程:
\[ \begin{gathered} \dot{\tilde{x}}(t)=A \tilde{x}(t)+B \tilde{u}(t) \\ \tilde{y}(t)=C \tilde{x}(t) \end{gathered} \]
显然将 \(\tilde{x}\) 带回零等同于将 \(x\) 带到 \(x_c\) 。因此,将 \(x\) 带回 \(x_c\) 的控制问题就是将 \(\tilde{x}\) 带回零的问题。可以如前所述,通过二次型优化问题来处理该问题,最小化为:
\[ J=\int_0^{\infty}\left(\tilde{x}^T Q \tilde{x}+\tilde{u}^T R \tilde{u}\right) d t \]
状态反馈矩阵 \(K\) 由Riccati方程给出,进行变量替换,得到:

\[ u(t)=-K\left(x(t)-x_c\right)+u_c \]
为了实现这种闭环控制,需要确定\(y_{\infty}=y_c\)时的\(\left(u_c, x_c\right)\)。为了显式呈现设定值,将上述结果改写为:
\[ u(t)=-K x(t)+e, e = u_c+Kx_c \]
其中\(e\)显然是个常数。写出闭环方程:
\[ \begin{gathered} \dot{x}(t)=(A-B K) x(t)+B e \\ y(t)=C x(t) \end{gathered} \]
与之前的步骤相同,在稳态时应有:
\[ \left\{\begin{aligned} &0=(A-B K) x_c+B e \\ &y_c=C x_c \end{aligned}\right.\Rightarrow \left\{\begin{aligned}&x_c=-(A-B K)^{-1} B e, \\ &y_c=-C(A-B K)^{-1} B e\end{aligned}\right. \]
解出:
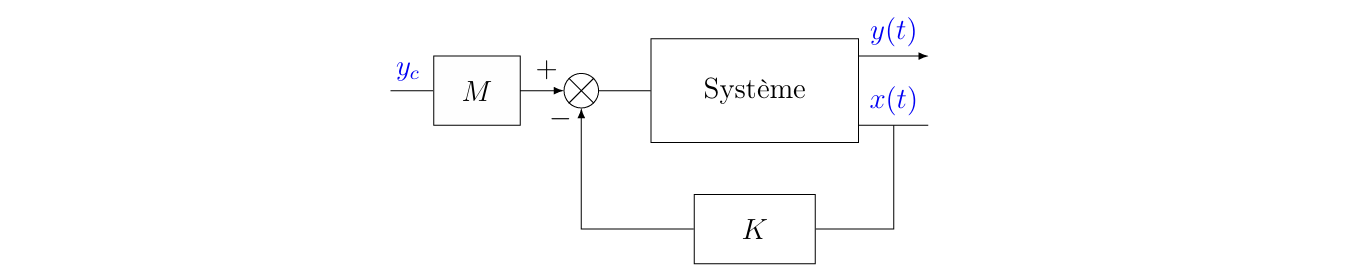
\[ e=-\left[C(A-B K)^{-1} B\right]^{-1} y_c=M y_c,M=-\left[C(A-B K)^{-1} B\right]^{-1} \]
恒定扰动的情况
在得到上述控制结构之后,可以将其应用在恒定扰动情况。考虑恒定扰动的系统:
\[ \begin{gathered} \dot{x}(t)=(A-B K) x(t)+B e+B^{\prime} d \\ y(t)=C x(t) \end{gathered} \]
基于完全相同的思路,可以得到:
\[ \begin{gathered}x_c=-(A-B K)^{-1} B e-(A-B K)^{-1} B^{\prime} d \\y_c=C x_c=-C(A-B K)^{-1} B e-C(A-B K)^{-1} B^{\prime} d\end{gathered} \]
解得:
\[ e=-\left[C(A-B K)^{-1} B\right]^{-1} y_c-\left[C(A-B K)^{-1} B\right]^{-1} C(A-B K)^{-1} B^{\prime} d \]
将其简化为:
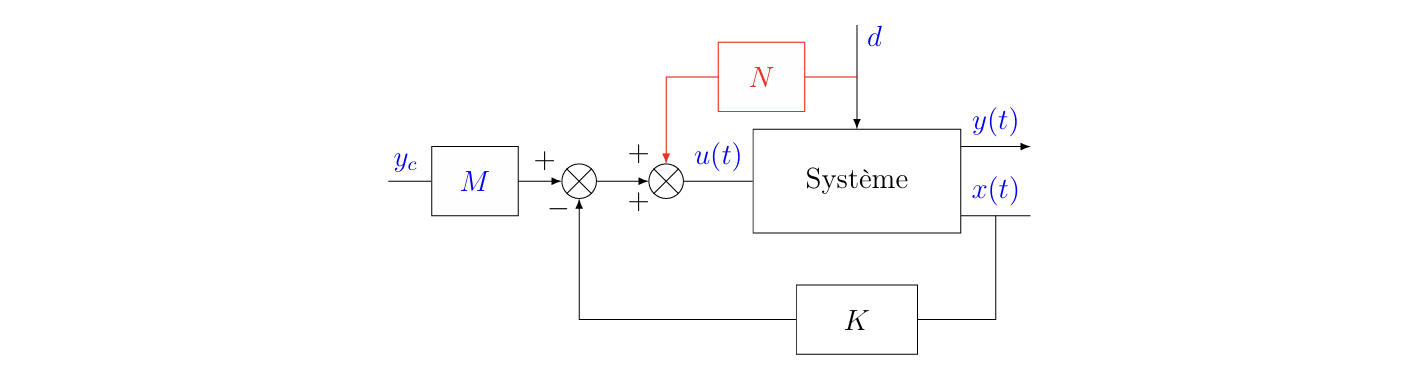
\[ e=M y_c+N d,M=-\left[C(A-B K)^{-1} B\right]^{-1}, \quad N=-\left[C(A-B K)^{-1} B\right]^{-1} C(A-B K)^{-1} B^{\prime} \]
C3.3.5 引入积分作用的LQ控制 Commande LQ avec action intégrale
另一种在稳态下消除扰动影响的解决方案是在控制律的综合中引入积分作用。
继续考虑状态:
\[ \begin{gathered} \dot{x}(t)=A x(t)+B u(t)+B^{\prime} d(t) \\ y(t)=C x(t) \end{gathered} \]
这里我们不再假设噪音恒定。预定义附加变量\(q(t)\),表示控制误差的积分:
\[ q(t)=\int_0^t\left(y(\tau)-y_c(\tau)\right) d \tau, \quad \frac{d q(t)}{d t}=y(t)-y_c(t) \]
定义增广状态向量\(x_a(t)=\left(x^T(t) \quad q^T(t)\right)^T\),原本的状态可以表示为:
\[ \begin{aligned} \binom{\dot{x}(t)}{\dot{q}(t)} & =\left(\begin{array}{ll} A & 0 \\ C & 0 \end{array}\right)\binom{x(t)}{q(t)}+\binom{B}{0} u(t)+\left(\begin{array}{cc} B^{\prime} & 0 \\ 0 & -I \end{array}\right)\binom{d(t)}{y_c(t)} \\ y(t) & =\left(\begin{array}{ll} C & 0 \end{array}\right)\binom{x(t)}{q(t)} \end{aligned} \]
引入偏差变量:
\[ \begin{aligned} & x^{\prime}=x-x_c \\ & y^{\prime}=y-y_c \\ & u^{\prime}=u-u_c \\ & q^{\prime}=q-q_c \end{aligned} \]
增广方程转换为:
\[ \begin{aligned}\binom{\dot{x}^{\prime}(t)}{\dot{q}^{\prime}(t)} & =\underbrace{\left(\begin{array}{ll}A & 0 \\C & 0\end{array}\right)}_{A_a}\binom{x^{\prime}(t)}{q^{\prime}(t)}+\underbrace{\binom{B}{0}}_{B_a} u^{\prime}(t) \\y^{\prime}(t) & =\underbrace{\left(\begin{array}{ll}C & 0\end{array}\right)}_{C_a}\binom{x^{\prime}(t)}{q^{\prime}(t)}\end{aligned} \]
问题重新转变为调节偏差变量\(y^{\prime}\)到\(0\),这可以通过闭环控制实现:
\[ u^{\prime}(t)=-K\binom{x^{\prime}(t)}{q^{\prime}(t)}=-K_1 x^{\prime}(t)-K_2 q^{\prime}(t) \]
可控性
在应用LQ控制之前,需要验证增广后的状态是否依然可控,即控制矩阵的秩是否为\(n+p\),控制矩阵:
\[ \mathcal{C}=\left(\begin{array}{ccccc}B & A B & A^2 B & \ldots & A^{n+p-1} B \\0 & C B & C A B & \cdots & C A^{n+p-2} B\end{array}\right)=\left(\begin{array}{cc}A & B \\C & 0\end{array}\right)\left(\begin{array}{ccccc}0 & B & A B & \ldots & A^{n+p-2} B \\I_m & 0 & 0 & \ldots & 0\end{array}\right) \]
为了使\(C\)的秩为\(n+p\),需要满足后两个矩阵的秩大于等于\(n+p\)。为此,需要满足:
- 秩 \(\left(\begin{array}{ll}A & B \\ C & 0\end{array}\right)=n+p\)
- \((A, B)\) 是可控的(这可确保出现在第二个矩阵的第一行上的矩阵构成的第二个矩阵的子矩阵的秩为\(n\))
- \(m\ge p\),这与前一个条件相结合,可确保第二个矩阵的秩为 \(n + m ≥ n + p\)。
注意,\(m\)是\(u(t)\)的维度,\(p\)是\(y(t)\)的维度,\(n\)是状态空间的维度。
假设状态可控,则可以应用LQ控制方法:
\[ \begin{aligned}& J=\int_0^{\infty}\left(x^{\prime}(t)^{\top} Q_1 x^{\prime}(t)+q^{\prime}(t)^{\top} Q_2 q^{\prime}(t)+u(t)^{\top} R u(t)\right) d t \\& \operatorname{avec} Q_a=Q_a^{\top}=\left(\begin{array}{cc}Q_1 & 0 \\0 & Q_2\end{array}\right) \geq 0 ; R=R^{\top}>0\end{aligned} \]
可检测性
为了应用LQ控制方法,需要保证\((A_a,B_a)\)可稳定且\((A_a,H_a)\)可检测,其中\(Q_a=H_a^{\top} H_a\),这在前一章已经讨论过。考虑模型:
\[ \begin{aligned}\binom{\dot{x}^{\prime}(t)}{\dot{q}^{\prime}(t)} & =\left(\begin{array}{ll}A & 0 \\C & 0\end{array}\right)\binom{x^{\prime}(t)}{q^{\prime}(t)}+\binom{B}{0} u^{\prime}(t) \\y_1(t) & =\left(\begin{array}{ll}H_1 & 0\end{array}\right)\binom{x^{\prime}(t)}{q^{\prime}(t)} \\y_2(t) & =\left(\begin{array}{ll}0 & H_2\end{array}\right)\binom{x^{\prime}(t)}{q^{\prime}(t)}\end{aligned} \]
其中\(H_1^T H_1=Q_1 , H_2^T H_2=Q_2\),为了保证可检测,要求:
- \((H_1,A)\)可检测
- \(rang(H_2) = p\)
满足可检测性和可控性之后,回到原始变量,闭环控制方程写做:
\[ u(t)=-K_1\left(x(t)-x_c\right)-K_2\left(q(t)-q_c\right)+u_c=-K_1 x(t)-K_2 q(t)+e \]
应用到原始系统得到:
\[ \begin{gathered}\dot{x}(t)=\left(A-B K_1\right) x(t)-B K_2 q(t)+B e+B^{\prime} d \\\dot{q}(t)=C x(t)-y_c \\y(t)=C x(t)\end{gathered} \]
由于\(e\)和\(d\)都是常数,状态向量最终趋于常数,因此\(\dot q(t)\rightarrow 0\),对比后两个方程,又有:
\[ y(t)\rightarrow y_c \]
无论\(e\)和\(d\)的取值。
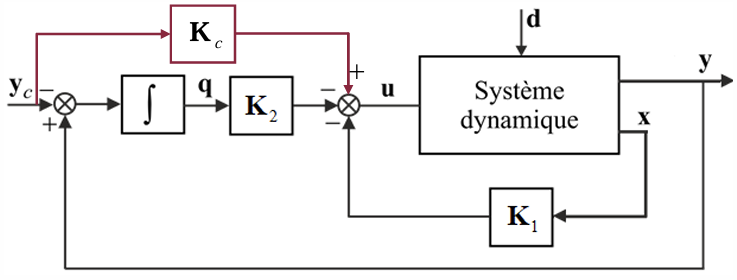
CE3.7 小车上的倒立摆
考虑倒立摆问题受到一定的噪音干扰,建立如下系统:
\[ \begin{aligned}\binom{\dot{x}^{\prime}(t)}{\dot{q}^{\prime}(t)} & =\underbrace{\left(\begin{array}{ll}A & 0 \\C & 0\end{array}\right)}_{A_a}\binom{x^{\prime}(t)}{q^{\prime}(t)}+\underbrace{\binom{B}{0}}_{B_a} u^{\prime}(t) \\y^{\prime}(t) & =\underbrace{\left(\begin{array}{ll}C & 0\end{array}\right)}_{C_a}\binom{x^{\prime}(t)}{q^{\prime}(t)}\end{aligned} \]
其中:
\[ A=\left(\begin{array}{cccc}0 & 0 & 1 & 0 \\0 & 0 & 0 & 1 \\0 & 10 & 0 & 0 \\0 & 22 & 0 & 0\end{array}\right), \quad B=\left(\begin{array}{l}0 \\0 \\1 \\2\end{array}\right), \quad C=\left(\begin{array}{llll}1 & 0 & 0 & 0\end{array}\right), \quad D=0 \]
观察LQ控制的条件:
- \(rang\left(\begin{array}{ll} A & 0 \\ C & 0 \end{array}\right) = n+p = 5\)
- \((A,B)\)可控
- \(m = 1 = p\)
- \(\left(H_a, A_a\right)\)可检测
考虑权重矩阵:
\[ Q=\left(\begin{array}{ccccc} 20 & 0 & 0 & 0 & 0 \\ 0 & 250 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 100 \end{array}\right), \quad R=1 \]
得到:
\[ K=\left(\begin{array}{lllll}-16 & 63 & -11.9 & 13.5 & -10\end{array}\right) \]